500 kV线路杆塔雷电冲击全波电磁暂态特性研究
甘 艳,姚 勇,张 昌,陈 柔,黄瑞莹
(1.华中电网有限公司,武汉 430077;2.武汉大学电气工程学院,武汉 430072)
0 引言
雷击电路杆塔放电过程是一个极为复杂的电磁过程,在地形复杂、多雷、土壤电阻率高的地区,雷击输电线路活动频繁,严重影响电网运行安全[1]。采用电磁场数值计算方法对输电线路、杆塔、接地极(或地网)进行统一建模分析是防雷技术研究发展的方向,同时,现代试验技术、计算机技术、电磁场计算理论的发展也为这一研究方向提供了保障。近几十年来,国内外在这方面做了大量的研究计算,取得了丰硕的研究成果[2-7]。
在早期建立模拟雷击的杆塔仿真模型中,通常采用等效电感来模拟杆塔,忽略杆塔上的波过程[8]。我国规程[9]给出了不同结构杆塔单位长度的电感值。将杆塔视为等值电感,杆塔上任意点的电位相同,不能完全反映雷击塔顶时雷电流在杆塔上的传播过程以及反射波对杆塔各节点电位的影响。随着电压等级[10]的不断提高,采用集中电感模拟杆塔的防雷性能的弊端越来越明显,计算结果也往往过于保守,造成线路建设投资过大。
在输电线路遭受雷击时,雷电流一部分从杆塔顶端流至底端,然后经过接地体装置向土壤散流,另一部分经过避雷线流向其他输电杆塔[11-12]。因此,塔顶过电压不仅受到杆塔自身电阻和冲击接地电阻的影响,还受到避雷线分流的影响,所以线路中避雷器也对雷击杆塔有所影响[13]。分析输电线路杆塔和接地装置的雷击冲击特性的前提是建立可靠的分析模型[14],这些模型都把外形和杆件复杂的杆塔,简化为等效圆柱或圆锥体等有规则的外形,并忽略了雷电流通过杆塔时产生的波形畸变和波速降低等因素的影响。此外,大地土壤电阻的存在,使得零电位并非在地面,但在理论计算中往往把地表面假设成零电位,计算结果也存在很大误差[15]。
因此,建立符合工程实际的输电线路、杆塔、接地极(或接地网)数学模型是输电线路防雷技术理论研究的基础。基于以上分析,本文通过CDEGS建立典型的输电线路-杆塔-接地极一体化计算模型,并从雷电冲击全波的观点对输电线路在雷电冲击下的电磁暂态特性进行深入研究,并分析不同土壤电阻率、雷电流参数时对杆塔电磁暂态特性的影响。
1 模型建立
选取典型500 kV酒杯型杆塔,杆塔型号为ZVB21b[16-17]。建立复杂精细模型,由于精细模型的计算量太大,必须要考虑模型的简化,由计算分析确定模型的简化程度,使其在保证准确度的同时减小计算量,加快计算速度。
1.1 模型简化
本文选用在CDEGS软件中的HIFREQ模块建立杆塔模型,因为HIFREQ模块中,适合计算细线模型,因此,把杆塔塔身的各类钢导体看作细线结构,各组成部分看作理想导体,由水平钢导体-横元,垂直钢导体-竖元,带有倾斜角度钢导体-斜元等细线元组合而成。通过ANSYS仿真可知,由于电荷的集肤效应,电流沿导体外表面流动,周长等效法的准确度更高,因此采用周长等效法,将杆塔塔身尺寸为50 mm×50 mm×70 mm角钢等效为15 mm圆柱形导体。接地装置采用方框带射线形式,6 m×6 m的方框和14.14 m射线均采用半径为7 mm的钢导体组成,并埋于地下0.8 m处。
将ZVB21b型酒杯模型分别在精细复杂模型基础上分别删去横元、斜元以及竖元,得到图1所示的4种简化模型。
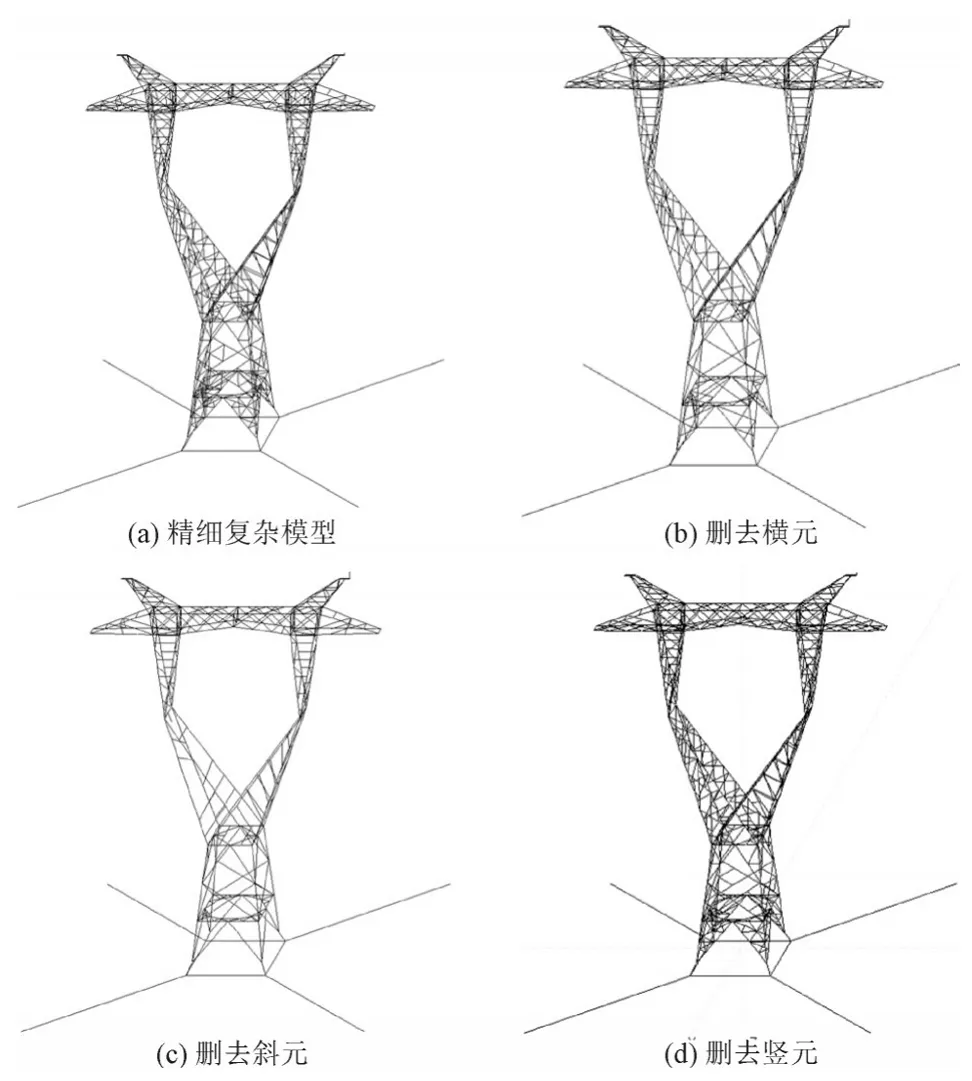
图1 不同简化模型图Fig.1 Difference simplified model
杆塔容易在塔顶处或避雷线上遭受雷击,在模型塔顶处加一段短导体作为注流点,因为这段导体的长度非常短,对计算结果不会造成影响,在注流点即塔顶处加上幅值为50 kA的雷电流,波前时间和半波时间为2.6μs和50μs,土壤电阻率选用2000Ω·m,对4种简化模型进行计算,本文暂不考虑火花效应,计算结束后分别选取4种模型塔顶注流点、横担以及塔脚4根引下线中一根导体电压值,其导体段的选取位置示例见图2,将4种模型计算数值进行比较。
仿真计算的横担、注流点以及引下线电压值见表1。计算可看出,删除横元之后,模型横担上的电位与精细模型横担上电位值最大仅相差0.7 kV,差值仅为0.022%,同时注流点和引下线上的电位差值最大也仅为0.024%左右。因此,可以认为横元对模型计算值影响不大,可以将横元在模型中略去。删除竖元之后的横担上电位与精细模型最大差值仅为0.66%,其余注流点和引下线的差值也在0.039%以内,因此可以认为竖元影响也不大。但是删除斜元之后的模型横担电位最大差值达到8.22%,注流点的点位差值也达到了13.22%,误差较大,因此要尽量避免简化斜元。
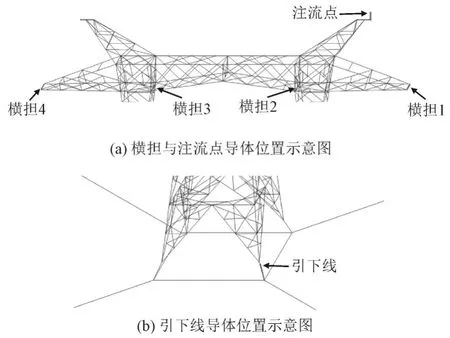
图2 选取导体位置示意图Fig.2 Schematic diagram of conductor position
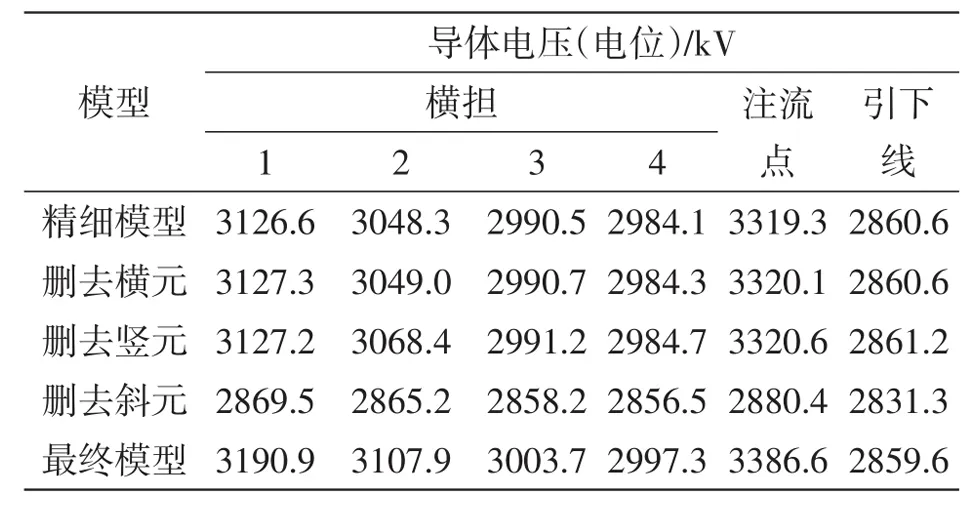
表1 不同模型导体电压值Table 1 Voltage values of different model conductors
为了减小计算量且保证计算精度在3%以内,对杆塔精细模型进行简化,通过上述计算,按照删去横元与竖元且尽量少删去一部分斜元的简化原则,得到的最终简化模型的横担电位值与精细模型最大相差2.05%,注流点和引下线电位值与精细模型最大相差2.02%。由此可见,通过简化竖元、横元以及斜元之后得到的模型,满足计算精度的要求。
1.2 确定杆塔基数
杆塔在遭受雷击时,通过避雷线分流,相邻的塔基具有分流的作用。因此,需要确定建立一体化模型中杆塔的基数。由于绝缘子串两端的电压为杆塔与线路运行电压差值,与导线无关,因此在模型设置中忽略导线,通过避雷线连接杆塔。考虑到计算量,本文中选用简化后杆塔一体化模型,考虑到500 kV输电线路由于500 kV线路档距较大,避雷线跨距长,避雷线选用LGJ-95/55系列钢芯铝绞线,档距400 m,建立输电线路-杆塔-接地体一体化模型。图3为输电线路-杆塔-接地体一体化模型示意图,中间杆塔为1号杆塔,右侧为2号杆塔,左侧分别为3号杆塔。在注流点处加上幅值为50 kA的雷电流,波前时间和半波时间为2.6 μs和50 μs,土壤电阻率选用500 Ω·m,雷电流击中线路1号杆塔顶端时,计算杆塔基数为单基、三基、五基、七基和九基时,1号杆塔靠近注流点处横担电位随时间的变化曲线,选择合适的杆塔基数。
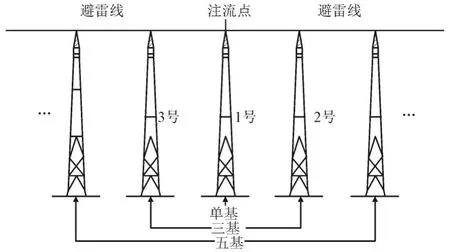
图3 输电线路-杆塔-接地体一体化模型示意图Fig.3 Schematic diagram of transmission line tower grounding system
计算结果见图4,当只有一基杆塔时,由于没有考虑避雷线的分流作用,横担上电位的最大值为7714.4 kV。杆塔基数为三基、五基、七基及九基杆塔时1号杆塔横担电位最大值分别为3528.7 kV、3659.8 kV、3400.9 kV、3514.3 kV。可以看出,三基、五基、七基及九基杆塔最大电位之间差别较小,但是当只建立一基杆塔时,最大电位与九基杆塔差值达到4200.2 kV,占52.8%。建立三基杆塔便可达到精算准确性,但是考虑到计算量和避雷线对于周围杆塔的分流作用,本文选用五基杆塔。

图4 不同杆塔基数时1号杆塔靠近注流点横担电位Fig.4 No.1 tower close to the point of the lateral load at different injection points
2 土壤电阻率对杆塔电磁暂态特性影响
500 kV输电线路众多,由于线路长,地处旷野,且地形、地势复杂,不少杆塔位于山顶或山脊,加上雷电活动频繁,极易遭到雷击,山区雷害事故要比平原地区高得多,严重影响了线路的安全运行,供电可靠性也随之下降。选典型的3种土壤电阻率500 Ω·m、1000 Ω·m和2000 Ω·m来模拟不同地区的土壤电阻率。
2.1 土壤电阻率对避雷线分流的影响
雷电流的分流作用会对杆塔横担冲击电压和接地电阻值有较大影响,本节主要分析土壤电阻率对雷电流分流作用的影响。
在注流点处加上幅值为50 kA,波前时间和半波时间为2.6 μs和50 μs的雷电流模拟雷电流击中线路1号杆塔顶端时,沿着1号杆塔至2号杆塔之间沿避雷线分流的电流和1号杆塔4根引下线其中一根流入大地的电流的变化。
由图5可看出,在不同土壤电阻率时避雷线上电流的变化趋势一致,先上升然后下降。土壤电阻率为500 Ω·m时,避雷线上电流在30 μs时达到最大值4.961kA,土壤电阻率1000Ω·m时,避雷线上电流在26 μs时达到最大值6.070 kA,土壤电阻率2000 Ω·m时,避雷线上电流在25 μs时达到最大值7.247 kA。随着土壤电阻率的增加,避雷线上电流最大值增加,达到最大值的时刻提前,且下降速度变快。图6为1号杆塔引下线上的入地电流随着土壤电阻率不同的变化趋势,均为先快速上升到达幅值再缓慢下降到零。随着土壤电阻率的增加,1号杆塔引下线电流峰值减小。

图5 不同土壤电阻率时避雷线电流Fig.5 Lightning current in different soil resistivity
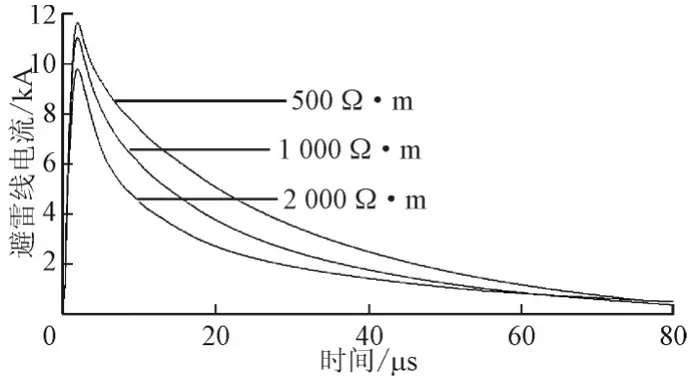
图6 不同土壤电阻率时引下线电流Fig.6 Downlead current of different soil resistivity
由此可知,随着土壤电阻率的增加,避雷线的分流作用越明显,雷电流沿避雷线流过的电流越多,传播越远,分流作用越强。
2.2 土壤电阻率对杆塔电压的影响
土壤电阻率会直接影响到接地电阻值的大小,从而直接影响接地体电压。图7为1号杆塔接地体电压随时间的变化趋势,不同土壤电阻率时接地体电压的变化趋势一致,均为快速上升到达幅值再逐渐减小到零,土壤电阻率为分别为500 Ω·m、1000 Ω·m和2000 Ω·m时接地体电压均在2.4 μs时达到最大值695.9 kV、1271.9 kV和2220.9 kV。当土壤电阻率较大时,虽然流过接地体的电流减小,但是电压还是大幅增加。
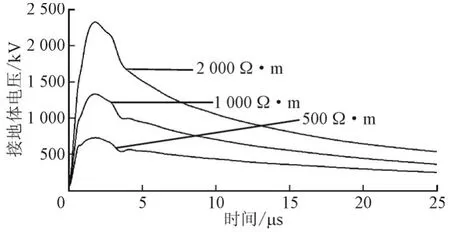
图7 不同土壤电阻率时接地体电压Fig.7 Ground voltage of different soil resistivity
图8 所示为1号杆塔靠近注流点处横担随时间的变化曲线,在土壤电阻率不同时均有相同的变化趋势,3条曲线均在0.8 μs和4 μs出现波谷,这是由于雷电流在避雷线上传播的时候会出现折射和反射的现象,雷电流与折反射的雷电流进行叠加而造成在电流逐渐减小的过程中出现电流增大的情况,这个过程伴随着雷电流散流的整个过程,后期由于雷电流快速衰减而减弱。土壤电阻率为500 Ω·m和1000 Ω·m时,由于土壤电阻率较低,雷电流通过接地体向大地散流快,横担电压下降过程较迅速,当土壤电阻率为2000 Ω·m,由于土壤电阻率较高,雷电流通过接地体向大地散流缓慢,在第一次下降较少时又与折反射过来的雷电流叠加反而上升到最大值附近。土壤电阻率分别为500 Ω·m、1000 Ω·m和2000Ω·m时,横担电压变化的趋势一致,均在0.6 μs快速上升电压最大值1583.4 kV、1847.2 kV以及2228.3 kV,直到雷电流完成全波过程下降到零。
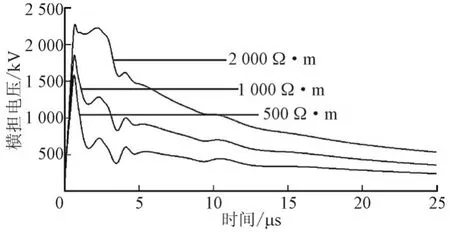
图8 不同土壤电阻率时横担电压Fig.8 Transverse voltage of different soil resistivity
3 雷电流对杆塔电磁暂态特性影响
在华中地区关于雷电流幅值地形差异化的研究中以葛岗线沿线走廊区域雷电为样本,将葛岗线沿线走廊地形划分为3种类型:平原、丘陵和山地,并统计各地形中雷电流幅值主要为50 kA、100 kA以及150 kA等,雷电流波前时间的分析选用国际标准2.6 μs,以及模拟其他情况下3.5 μs和7 μs,半波时间均为50 μs,土壤电阻率选用1000 Ω·m的地区进行仿真。
3.1 雷电流幅值对避雷线分流的影响
在注流点处加上幅值分别为50 kA、100 kA以及150 kA雷电流模拟不同雷电流幅值下击中线路1号杆塔顶端,分析沿着1号杆塔至2号杆塔之间沿避雷线分流的电流和1号杆塔引下线流入大地的电流变化。
如图9所示,随着雷电流的幅值增加,避雷线上电流曲线均在25 μs时达到最大值6.1 kA、12.2 kA以及18.3 kA。由此可看出,雷电流幅值增加一倍时,避雷线峰值也增加一倍,雷电流幅值增加两倍时,避雷线峰值也增加两倍,雷电流幅值与避雷线峰值为线性关系。
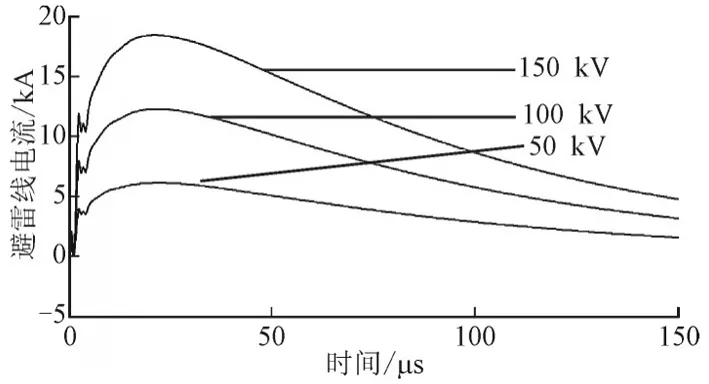
图9 不同雷电流幅值时避雷线电流Fig.9 Lightning current of different lightning current amplitude
图10 所示为不同雷电流幅值下的引下线电流,3条曲线同时在2.4 μs时达到电流最大值分别为10.5 kA、21.1 kA以及31.7 kA,引下线流入大地散流的电流峰值也与雷电流幅值呈倍数增长且电流幅值越大,引下线电流下降时斜率越大。
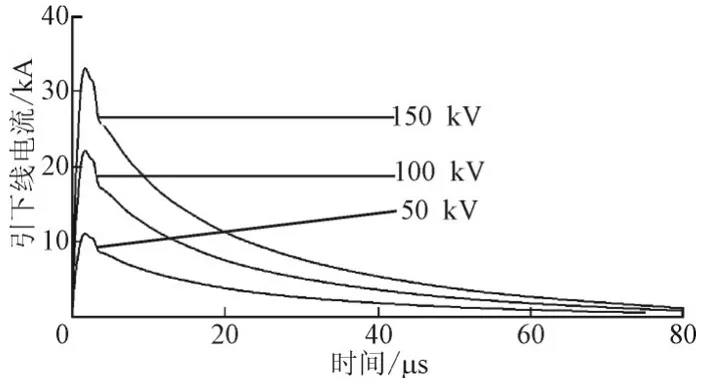
图10 不同雷电流幅值时引下线电流Fig.10 Downlead current of different lightning current amplitude
3.2 雷电流幅值对杆塔电压的影响
雷电流幅值的改变通过改变流过避雷线以及杆塔接地体的电流大小影响杆塔横担以及接地体的电压。
图11、图12分别为不同雷电流幅值时接地体以及横担电压变化曲线,雷电流幅值为50 kA、100 kA以及150 kA时接地体电压均在2.4 μs时达到最大值1271.9 kA、2548.2 kA和3827.6 kA;横担电压均在0.6 μs时达到最大值1847.2 kA、3692.7 kA和5535.1 kA。可以看出改变雷电流的幅值,1号杆塔的接地体电压和横担电压在在不同雷电流幅值下变化趋势基本完全一致,主要影响电压最大幅值呈倍增长。

图11 不同雷电流幅值时接地体电压Fig.11 Grounding voltage of different lightning current amplitude

图12 不同雷电流幅值时横担电压Fig.12 Transverse voltage of different lightning current amplitude
3.3 波前时间对避雷线分流的影响
将波前时间分别改为2.6 μs、3.5 μs以及7 μs,仿真得到的避雷线上电流曲线变化见图13,3条避雷线上电流基本完全重合,由此可知,波前时间对避雷线分流的影响较小。
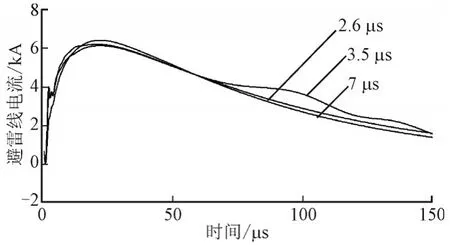
图13 不同波前时间时避雷线电流Fig.13 Lightning current at different wave front time
3.4 波前时间对杆塔电压的影响
为了分析波前时间对杆塔电压的影响,分别选取2.6 μs、3.5 μs以及7 μs进行仿真,选取1号杆塔上的接地体以及横担电压进行分析。
图14和图15分别为不同波前时间时接地体以及横担电压的变化曲线。波前时间为2.6 μs和3.5 μs时,接地体电压均在在2.4 μs时达到最大值1272.0 kV和1251.1 kA,横担电压同样在0.6 μs时达到最大值1847.2 kA和1507.5 kA;波前时间为7 μs时接地体电压在2.9 μs时达到最大值1046.6 kA,横担电压在2.6 μs时达到最大值1125.2 kA。接地体电压曲线在波前时间改变时变化趋势较一致,横担电压曲线在波前时间为2.6 μs和3.5 μs时变化趋势较一致,波前时间改为7 μs曲线最大幅值降低较多,且全波过程中的波动幅度较小,在3条曲线第一个波谷的出现时刻随着波前时间的增大而延后。

图14 不同波前时间时接地体电压Fig.14 Ground voltage of different wave front time
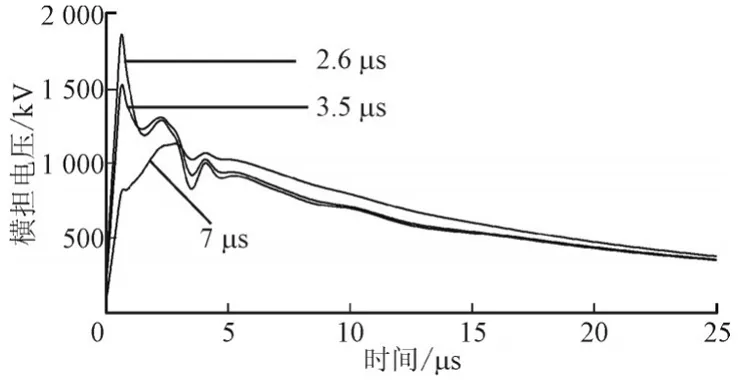
图15 不同波前时间时横担电压Fig.15 Transverse voltage of different wave front time
由此可知,改变波前时间会影响接地体电压和横担电压峰值且对波形的波峰波谷出现时刻也有一定的影响。改变波前时间较少时,对电压峰值幅值大小以及波峰波谷的出现时刻的影响较小,当改变较大时,对电压峰值幅值大小以及波峰波谷的出现时刻的影响较大。
4 结论
1)CDEGS软件中的HIFREQ模块中建立ZVB21b酒杯型杆塔模型,杆塔模型的横元、竖元对于模型简化影响较小,斜元的影响较大,杆塔的基数选用5基能保证计算精度与避雷线的分流效果。
2)雷击1号杆塔塔顶时流经2号杆塔的避雷线分流的电流,受土壤电阻率和雷电流幅值的影响较大,但受波前时间的影响较小,土壤电阻率越大,避雷线分流电流峰值越大,下降速度也越快;雷电流幅值增加,避雷线上电流也基本呈线性增加。
3)通过引下线向土壤中散流的电流随着土壤电阻率的增大而减小,随着雷电流幅值的增加线性增加。
4)接地体电压曲线和横担电压曲线均随着土壤电阻率的增加而增加,随着雷电流幅值的增加而增加,而不会改变出现峰值的时刻。改变波前时间较少时,对电压峰值幅值大小以及波峰波谷的出现时刻的影响较小,当改变较大时,对电压峰值幅值大小以及波峰波谷的出现时刻的影响较大。

