氧化锌电阻片冲击电流下残压特性方程的研究
桑建平,田泽群,杨 涛,张 悦
(1.西安高压电器研究院有限责任公司,西安 710077;2.国网浙江省电力有限公司电力科学研究院,杭州 310014;3.国网河南省电力公司荥阳市供电公司,河南荥阳 450100)
0 引言
1968年,日本松下公司发明了具有优良非线性和优异能量吸收能力的氧化锌压敏陶瓷。近50年来,科技工作者们对这种新材料进行了大量的基础研究和技术开发,其性能不断提升,在电力系统、防雷工程、电子设备和系统、微电子设备和系统等多个领域得到广泛应用[1]。
金属氧化物避雷器(metal oxide arrestor,MOA),采用了氧化锌压敏陶瓷做为核心元件,它能有效降低电力系统在非正常运行状态下出现的过电压和大电流幅值,是电力系统中重要的保护电器之一。
MOA的残压特性对电力系统的绝缘水平和运行可靠性有着至关重要的影响。而MOA的残压特性很大程度上由它的核心元件——氧化锌压敏陶瓷(亦称压敏电阻片、ZnO非线性电阻片或氧化锌电阻片)的特性所决定[2]。
目前,各种类型MOA的现行国家以及国际标准均明确指出:测量残压的目的是为获得各种规定的电流和波形下某种给定设计的最大残压。在制造厂资料中必须规定并公布例行试验用雷电冲击电流下最大残压,电流幅值是0.01~2倍标称放电电流范围内任一适当的值[3]。为此,MOA制造厂应该非常熟悉所生产或外购的各种规格的氧化锌电阻片的雷电冲击电流下残压特性。
在氧化锌电阻片残压测试方面,要求两次放电的间隔时间应足使试品恢复到接近环境温度[3]。实际上,在进行残压试验时,每一次都能准确地测定某一规定电流下的残压是非常困难的,往往需要对氧化锌电阻片施加多次冲击电流才能成功完成某一规定电流下的残压测试,这无疑大大降低了测试效率。即使通过不断穿插替换新电阻片进行试验,表面上测试效率得到了提高,但是测量用分压器经过长期不间断工作,其内部会产生温升。当温度达到一定程度后,测量准确度会不断下降,从而也会导致残压测量值误差的不断增加。
为此,国内外学者对于冲击电流脉冲下的氧化锌电阻片特性进行过多方面的研究。
文献[4]通过研究多种型号规格的氧化锌电阻片,拟合出“脉冲欧安(Ω-A)特性方程”,变换得到一种氧化锌电阻片脉冲V-I特性方程:
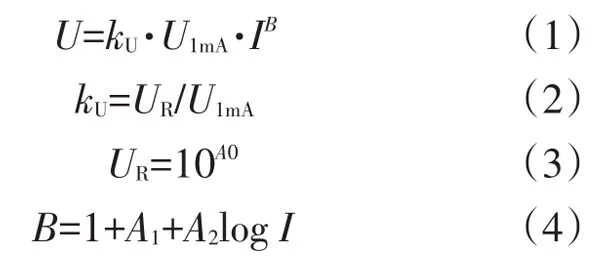
式中:U1mA是被测试样品在直流1mA参考电流下的“直流参考电压”;A0,A1和A2是常数,数值取决于电阻片的型号规格和制造水平。
然而,笔者在2005年就曾指出:由于配方、烧成工艺的不同,会导致规格相同的电阻片参数存在一定的差异;另外,大多数氧化锌电阻片生产厂家在原料的纯化、细化、配方、混料以及制坯、烧成等工艺技术及控制上也无法做得非常完善,或多或少的人为因素也会使同一批次电阻片的电气参数存有差异[5]。因此,该特性方程作为常数的A0,A1和A2,对于不同厂商、不同批次的电阻片而言,实际上是3个动态变化的量,必须先选取5片以上的该批次电阻片进行试验,以测定该批次电阻片的A0,A1和A2常数,才能再运用特性方程进行校正或验证,实用性并不高。
文献[6]给出了氧化锌电阻片的电压-电流特性的近似公式:

式中:I为流过氧化锌电阻片的电流;U为氧化锌电阻片两端的电压;C、α为与材料有关的常数。α值也称非线性系数,可通过测定流过电阻的电流I1和I2及其所对应的电压U1和U2,按 α =(lgI1-lgI2)/(lgU1-lgU2)=lg(I1/I2)/lg((U1/U2)求解,通常对于氧化锌电阻片来讲,典型的α值在30~100[7]。众所周知,不同电流区域内的氧化锌电阻片的V-I特性并不相同,如果电流I1和I2取值跨越了不同区间,α值就会出现较大偏差。另外,通常情况下,在预冲击一次后,可以根据电流幅值调整设备的充电电压,再经过1次或2次冲击,即可得到预期电流下的残压值,这要比先预冲击两次,计算出α值,再代入近似公式求取预期电流下的残压值要准确、便捷得多[8]。
笔者长期从事避雷器产品的检测工作,通过日常大量的试验和研究发现:氧化锌电阻片虽然在不同电流区域内的V-I特性不同,但在每一个特定的电流区域内,某一特定系数与电阻片的直径存在近似线性关系的,该特定系数与电阻片横截面的表面积、厚度、压比值有关。
1 试验方案与数据
笔者选取直径为ϕ35~ϕ61 mm 5种不同生产厂商的新电阻片,测试在标准雷电冲击电流和操作冲击电流下不同电流幅值下的电阻片残压。对于每种规格的电阻片,笔者选取了具有不同直流参考电压U1mA的新电阻片并尽可能多的反复测试,并且按照电流值从小到大和从大到小的不同序列进行,两次电流冲击之间尽量使电阻片冷却至接近环境温度。5种规格氧化锌电阻片某次测量的数据见表1和表2。
从表1和表2的数据可看出:随着电阻片直径的增加,其压比逐渐变小。
2 数据处理与分析
研究表明:氧化锌电阻片的残压值与电阻片横截面的表面积、厚度以及电流幅值等密切有关。电阻片横截面的表面积越大,厚度越薄,冲击电流值越低,残压值也越低。
将表1和表2中的残压压比Ky与该规格电阻片横截面的表面积s相乘,然后再除以该规格电阻片的厚度h,得到一个固有系数M(即M=Ky×s/h)。将雷电冲击电流按2.5 kA以下,2.5~5 kA,5 kA以上,操作冲击电流按250 A以下,250~500 A,500 A以上分区间,分别计算各区间ΔM与ΔI的比值,即特性系数K:

式中:I1、M1指电流值为I1时对应的特性系数 M1;I2、M2指电流值为I2时对应的特性系数M2,这里I1、I2取各区间的最小电流值和最大电流值,得到表3和表4。
从表3和表4的计算结果可明显看出:随着电阻片直径的增加,其固有系数M逐渐变大,特性系数K逐渐减小。
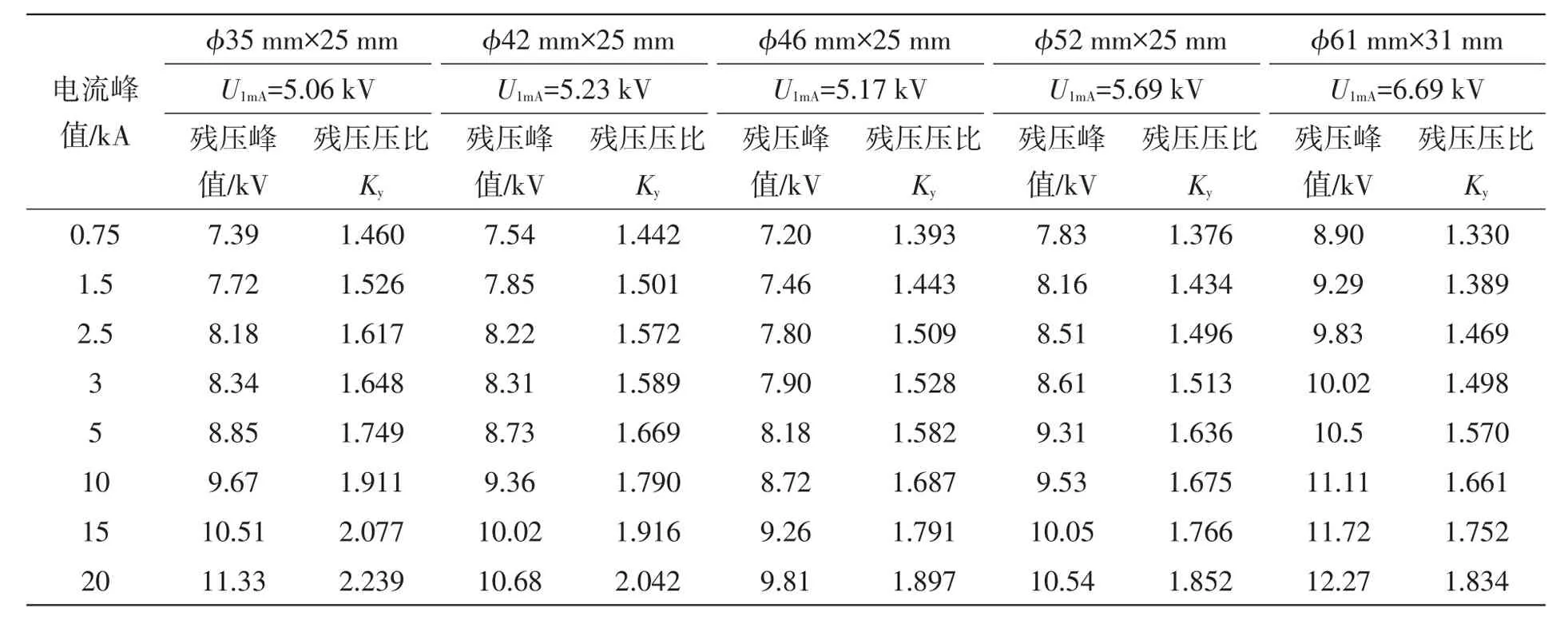
表1 氧化锌电阻片的8/20 μs雷电冲击残压实测数据Table 1 Data of the 8/20 μs lightning impulse residual voltage for ZnO resistor
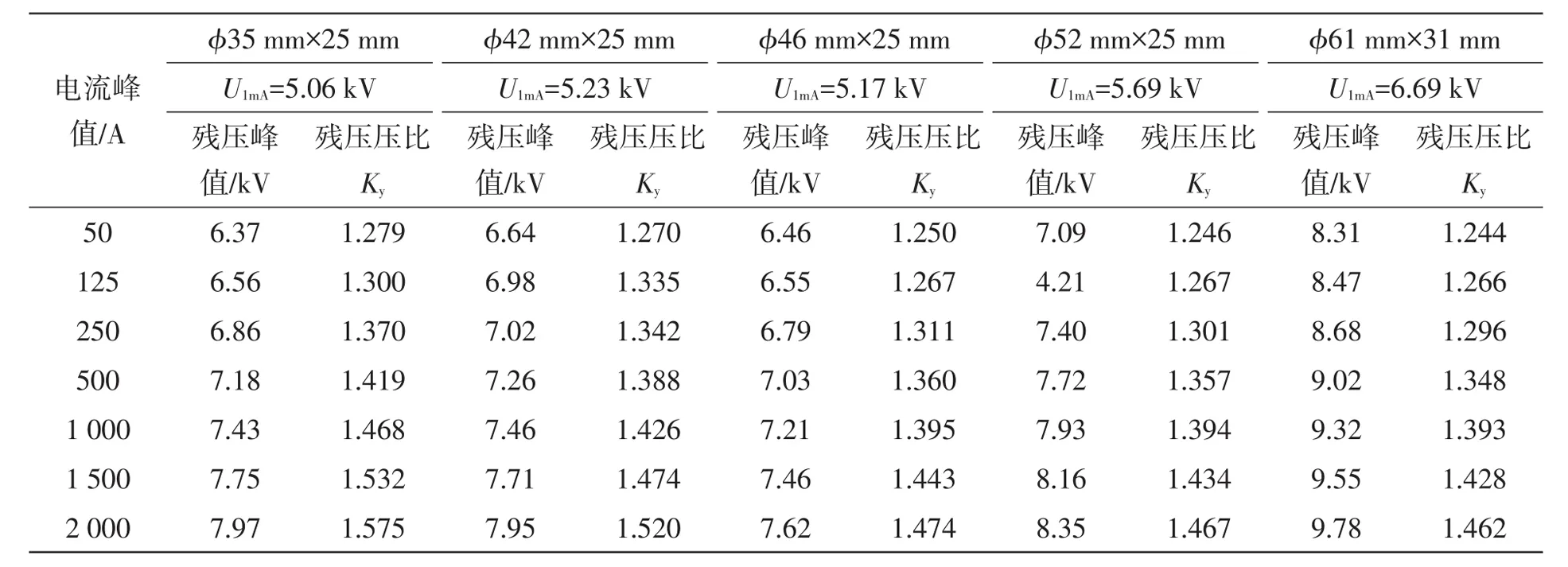
表2 氧化锌电阻片40/100 μs操作冲击残压数据Table 2 Data of the 40/100 μs switching impulse residual voltage for ZnO resistor
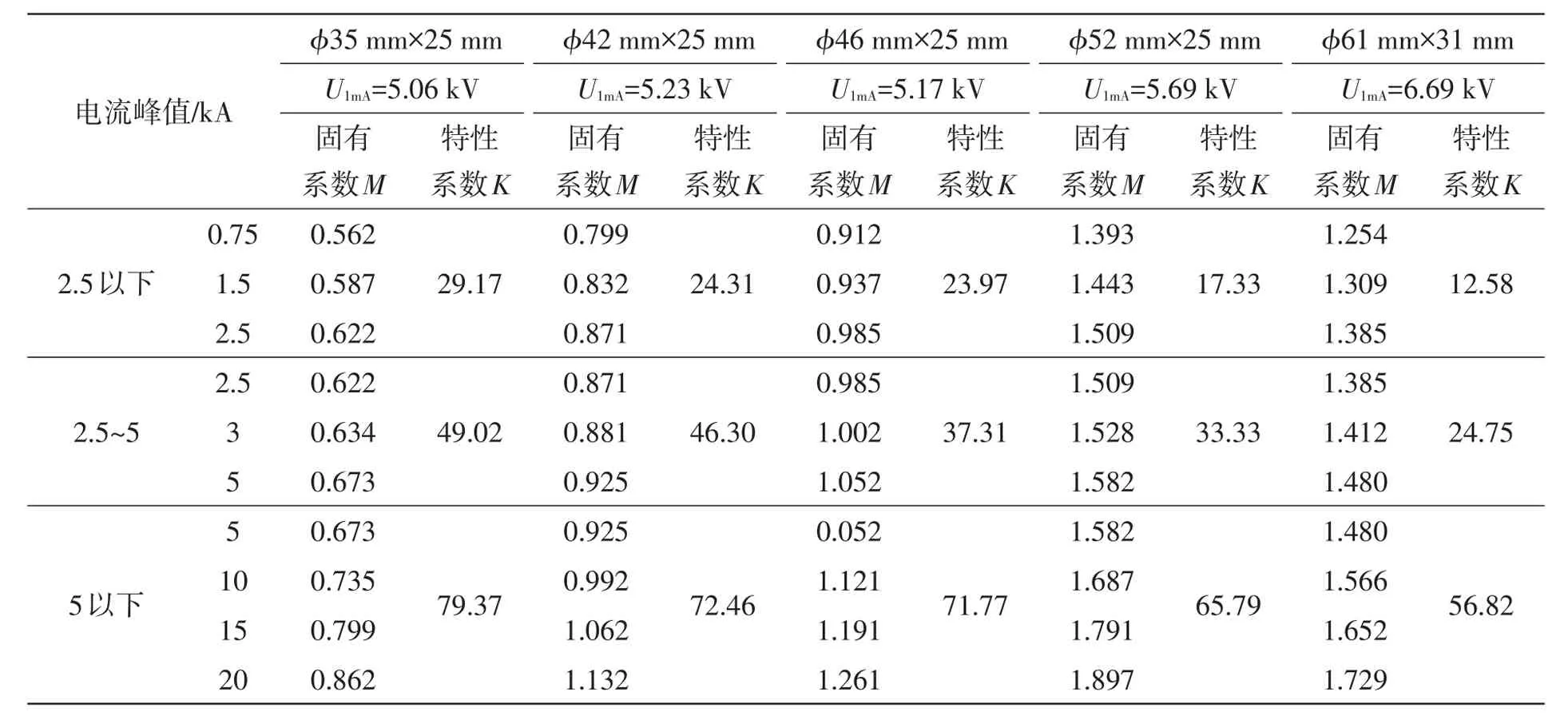
表3 氧化锌电阻片8/20 μs雷电冲击残压下的系数M及K值Table 3 Coefficient k and M of 8/20 μs lightning impulse residual voltage for ZnO resistor

表4 氧化锌电阻片40/100 μs操作残压下系数M及K值Table 4 Coefficient k and M of 40/100 μs switching impulse residual voltage for ZnO resistor
研究还发现:电阻片的U1mA是随冲击次数的增加而不断下降的。运用双肖特基势垒理论可以解释这种现象:冲击初期,注入的电子被氧化锌电阻片微晶结构中晶界处的陷阱俘获而不能到达反偏侧,而反偏侧肖特基势垒中的空穴使费米能级降低,引起反偏侧的势垒高度有所增加,从而使电子跃迁所需要的能量增加,宏观上表现为U1mA的小幅上升。
随着冲击次数的增加,注入的电子将正偏侧晶界处的陷阱填满,进而不断向反偏侧迁移,反偏侧肖特基势垒的费米能级不断上升,晶界势垒高度下降。同时,大量注入的能量导致氧化锌电阻片内部产生较高的温度,在热激发作用下晶界层以及耗尽层中的离子的迁移开始变得活跃,反偏耗尽层中的锌离子向反偏界面方向移动,同表面态发生中和反应,进一步降低了反偏势垒高度,在宏观上表现为U1mA的缓慢降低。
随着冲击次数的进一步增加,使氧化锌电阻片内部的温度持续升高,肖特基势垒高度下降,晶界击穿电压也随之下降,部分导热性能较差的晶界在热效应作用下垮塌,局部形成一个低阻值区域。冲击电流流经该区域,导致局部温度继续攀升,引起该区域晶粒表面的熔穿或者晶粒之间的熔合,晶界数量减少以及晶界势垒高度下降,在宏观上表现为U1mA的快速降低。
每次电流冲击后,电阻片U1mA的测量准确度会受试品温度、测量时机、电流冲击的幅值等诸多因数影响,因此,本文在计算残压压比时,采用的是未经电流冲击的新电阻片的U1mA。
需要说明的是:氧化锌电阻片的残压压比是由晶界数量以及其势垒高度决定的,与晶粒尺寸的大小关系不大。这就是在整个电流冲击过程中,即使氧化锌电阻片的晶粒遭受到严重损坏,残压值也没有显著变化的根本原因。
经过大量试验并对试验数据进行统计,得到氧化锌电阻片雷电残压的特性系数K值表,见表5。操作残压的特性系数K值表。见表6。
分别将表5和表6中的电阻片直径作为横轴,特性系数K作为纵轴,分别得到各个电流区间的特性系数K值与电阻片直径的关系图,见图1和图2。可以明显看出各个电流区间的特性系数K值呈线性关系,即K=-ax+b。

表5 氧化锌电阻片8/20 μs雷电冲击残压特性系数KTable 5 Characteristic coefficient K of 8/20 μs lightning impulse residual voltage for ZnO resistor

表6 氧化锌电阻片40/100 μs操作冲击残压特性系数KTable 6 Characteristic coefficient K of 40/100 μs switching impulse residual voltage for typical specifications ZnO resistor
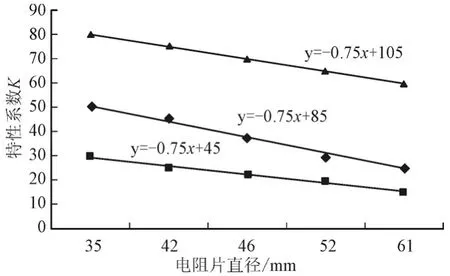
图1 不同电流区间的雷电冲击残压特性系数K与电阻片直径关系图Fig.1 Relationship between characteristic coefficient K of lightning impulse residual voltage and diameter of resistor

图2 不同电流区间的操作冲击残压特性系数K与电阻片直径关系图Fig.2 Relationship between characteristic coefficient K of switching impulse residual voltage and diameter of resistor
通过对各条线性曲线拟合,可以得到雷电冲击电流如下:
电流值在2.5 kA以下(第1区间)时,a=0.55,b=45,即K=-0.55x+45;
电流值在2.5~5.0 kA之间(第2区间)时,a=0.95,b=85,即K=-0.95x+85;
电流值在5.0 kA以上(第3区间)时,a=0.75,b=105,即K=-0.75x+105。
操作冲击电流下:
电流值在250 A以下(第1区间)时,a=50,b=7000,即K=-50x+7000;
电流值在250~500 A之间(第2区间)时,a=250,b=20000,即K=-250x+20000
电流值在500 A以上(第3区间)时,a=450,b=40000,即K=-450x-40000
3 结论
1)随着电阻片横截面表面积的增加,其固有系数M缓慢增加,特性系数K缓慢降低。经过同极性或不同极性的多次电流冲击后,电阻片在同一电流值下的残压值变化不大。
2)氧化锌电阻片的残压值与电阻片横截面的表面积、电阻片厚度以及压比密切有关。在配方和工艺相同的情况下,电阻片横截面的表面积越大,厚度越薄,残压越低。
3)在不同的冲击电流幅值区间内,电阻片的雷电或操作冲击残压特性系数K(与该电阻片的横截面的表面积、厚度和压比有关)与电阻片的直径x存在近似的线性关系:K=-ax+b,a和b在各区间内为常量。
这里需要说明的是残压特性系数K的线性近似公式仅适用于残压估算该线性关系式是通过对大量的试验数据拟合得到的,那些经过了工频或冲击的已老化电阻片,或者是具有高梯度等的特殊电阻片,可能会出现偏差较大的情况。另外,实际电流值与分界电流值越远,估算值偏差越大;反之,实际电流值与分界电流值越近,估算值偏差越小。
按照避雷器相关国家及国际标准的技术要求,残压还应包括陡波冲击电流下(电流波形为1/5 μs或1/10 μs)的残压,笔者经初步研究发现,在不同的冲击电流幅值区间内,陡波冲击电流下的残压特性系数K与电阻片的直径依然存在近似的线性关系,待笔者做进一步的研究和验证后,在后续的文章中会予以介绍和阐明。
运用该线性公式,可以很好地修正因冲击电流幅值偏差对电阻片残压的影响,大幅减少为测定特定电流幅值下残压的冲击次数,有效提高残压测试数据的准确性,降低避雷器整体残压的偏差。

