基于ABAQUS软件的二维车辆-轨道耦合模型

蒋崇达 唐 娟

(1. 中铁房地产集团华东公司合肥事业部， 230031， 合肥； 2. 合肥铁路工程学校， 230011， 合肥//第一作者， 工程师)

ABAQUS软件可以分析复杂的刚柔体力学系统，处理高度非线性问题。文献[1]、文献[2]等基于ABAQUS软件建立了铁道车辆-轨道空间耦合动力学模型。鉴于显式算法求解，钢轨有限元模型的网格尺寸不能划分得太小，导致很难考虑到轨道短波不平顺的影响。本文提出的一种基于ABAQUS软件的10个自由度多刚体整车-浮置板轨道二维有限元模型，主要用于考虑车辆-轨道耦合系统竖向振动时的数值分析。该模型的2个子系统通过非线性赫兹接触实现轮轨互制，采用隐式求解，可以将钢轨有限元模型的网格尺寸划分得足够小，从而可考虑轨道短波不平顺的影响及求解耦合系统的振动问题。相比空间耦合模型，该模型建模简单，计算效率更高。

1 计算模型及参数

1.1 车辆-轨道有限元模型

将车厢、转向架及轮对均考虑为刚体模型，采用结构质量单元(MASS)模拟；悬挂系统使用弹簧阻尼单元模拟；车厢、转向架均考虑转角和沉浮运动，轮对仅考虑沉浮运动。整车模型共10个自由度，如图1所示。车辆参数采用地铁B型车参数[3]。钢轨、浮置板、隧道均选用梁单元(B21)；钢轨采用CHC60型钢轨；扣件采用弹簧阻尼单元，间距0.625 m，刚度值为60 kN/mm，阻尼值为5×104N·s/m；浮置板截面尺寸为3.38 m×0.40 m；支座采用弹簧阻尼单元模拟，刚度值为6.9 kN/mm，阻尼值为7.5×104N·s/m，间距1.25 m；隧道视为弹性支撑在文克尔地基上的长梁，隧道衬砌外径3 m，壁厚0.3 m，基础等效刚度为36×106N/m[4]。边界条件设定钢轨、轨道板及隧道梁为简支约束，地基底部节点为全约束。

a) 10个自由度车辆-双层梁轨道耦合模型

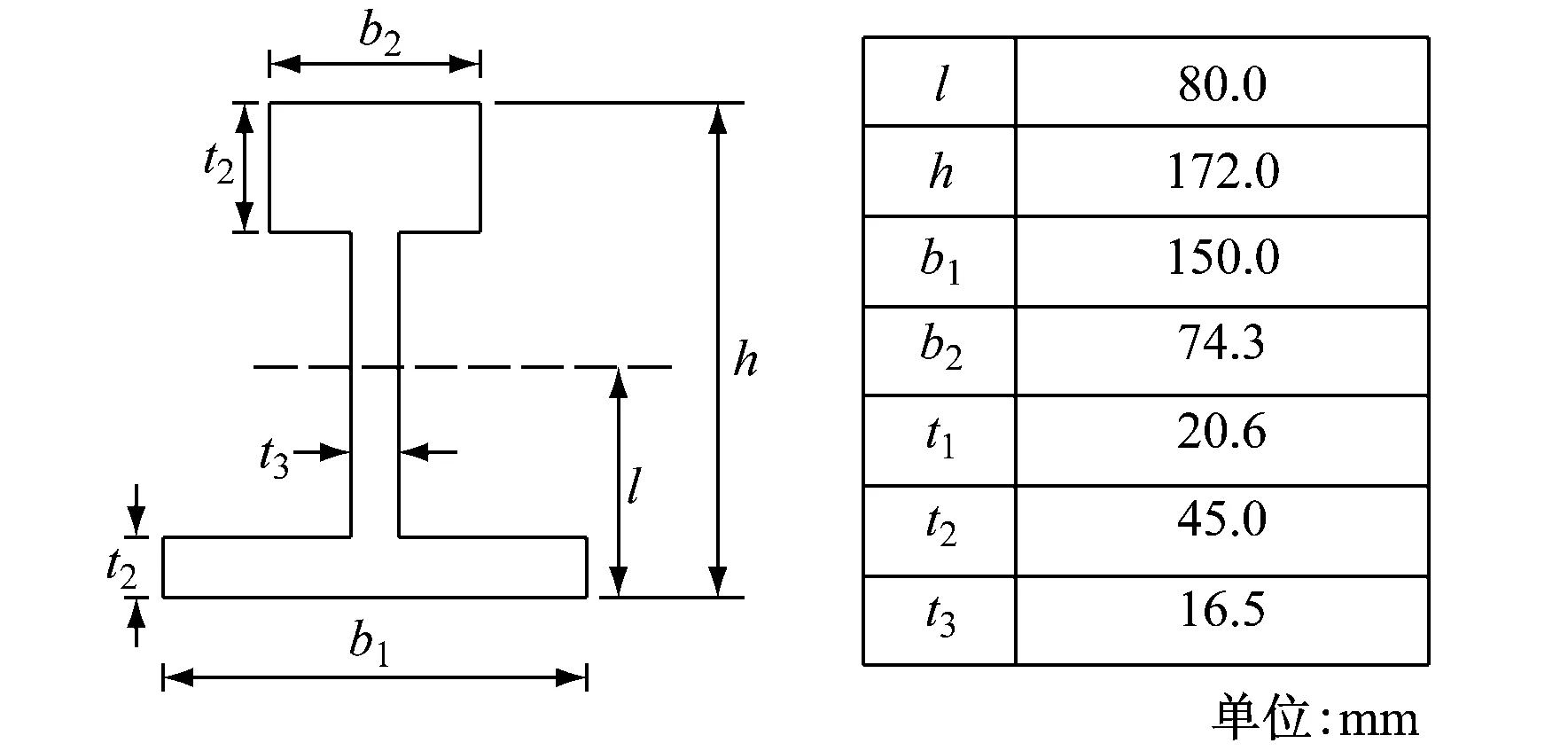
b) CHC60钢轨近似断面尺寸图1 车辆-浮置板式轨道的轮轨耦合模型

显示算法较隐式算法的优势在于，以较小的时间成本代价换取更大的计算规模。由于显式算法的计算成本与模型中最小网格尺寸成反比，所以在基于ABAQUS软件的车辆-轨道空间模型中，钢轨有限元模型的纵向网格尺寸一般控制在0.060～0.300 m之间(见图2 a))，否则过小的网格尺寸将大大降低计算效率。本文为考虑短波不平顺的引入，采用隐式算法建立计算模型，且考虑到计算规模问题，钢轨有限元模型的网格尺寸可取0.002 m(见图2 b))，浮置板和隧道梁有限元模型的网格尺寸取0.1 m。

1.2 轮轨接触模型

定义车轮节点为接触从面(slave surface)，轮轨耦合通过接触模块实现。ABAQUS软件中，采用单纯的主-从算法时，从面节点不能侵入主面任何部分，但主面节点可以侵入从面，即轮轨间并不会发生相互侵入(这是符合逻辑的)。

轮轨法向接触模型中，由Hertz非线性弹性接触理论[5]确定接触力与轮轨弹性压缩量关系后，通过力-位移的表格形式导入ABAQUS软件中接触属性参数，即摩擦系数取0.3，滑动容差系数取0.005。

1.3 轨道不平顺及数值模拟

轨道不平顺是影响结构振动频率特性的主要因素[6]。鉴于城市轨道交通轨道不平顺并没有合适的功率谱表征，故本文模型中：1.00～50.00 m中长波不平顺采用经典的美国六级谱，0.01～1.00 mm短波不平顺采用日本Sato谱。采用频域内功率谱等效算法得到轨道不平顺模拟样本，通过自编Matlab程序在inp文件中修改钢轨节点的竖向坐标值，从而实现轨道不平顺的引入。

a) 三维空间模型中钢轨有限元模型的网格划分

b) 二维模型中钢轨有限元模型的最小网格尺寸图2 ABAQUS软件车辆-轨道空间模型中钢轨有限元 模型的网格划分

2 模型计算及验证

使用有限元方法进行结构振动计算，可以得到在轮轨互制作用下结构随时间变化的节点位移、速度和加速度的响应，其基本方程为：

[M][a]+[C][v]+[K][u]=[F]

(1)

式中:

[M]、[C]、[K]——结构质量矩阵、阻尼矩阵、刚度矩阵；

[a]、[v]、[u]——结构振动加速度、速度、位移；

[F]——荷载向量。

本文选用隐式算法求解器对式(1)进行求解。

2.1 模型验证(1)

采用SIMPACK软件验证本文模型上部车辆系统的正确性，其参数采用地铁B型车参数[3]，车速设为20 m/s。多刚体整车多体系统动力学(MBS)模型见图3 a)。引入轨道不平顺(波长范围0.01～50.00 m)，车速设为20 m/s。本文模型采取相同参数及不平顺样板，通过对比竖向轮轨力结果，验证模型正确性。

计算结果见图3。由图3可见，引入轨道不平顺后，竖向轮轨力发生了较大幅度的振荡。其中，SIMPACK软件计算的轮轨力范围在55.0～75.0 kN，本文模型计算的轮轨力范围在52.5～78.0 kN。可见两种模型引入不平顺后轮轨力的变化趋势和变化幅度基本一致，由此验证了本文模型的正确性。

a) SIMPACK软件整车MBS模型

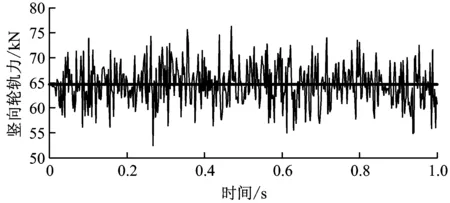
b) SIMPACK软件模型计算结果

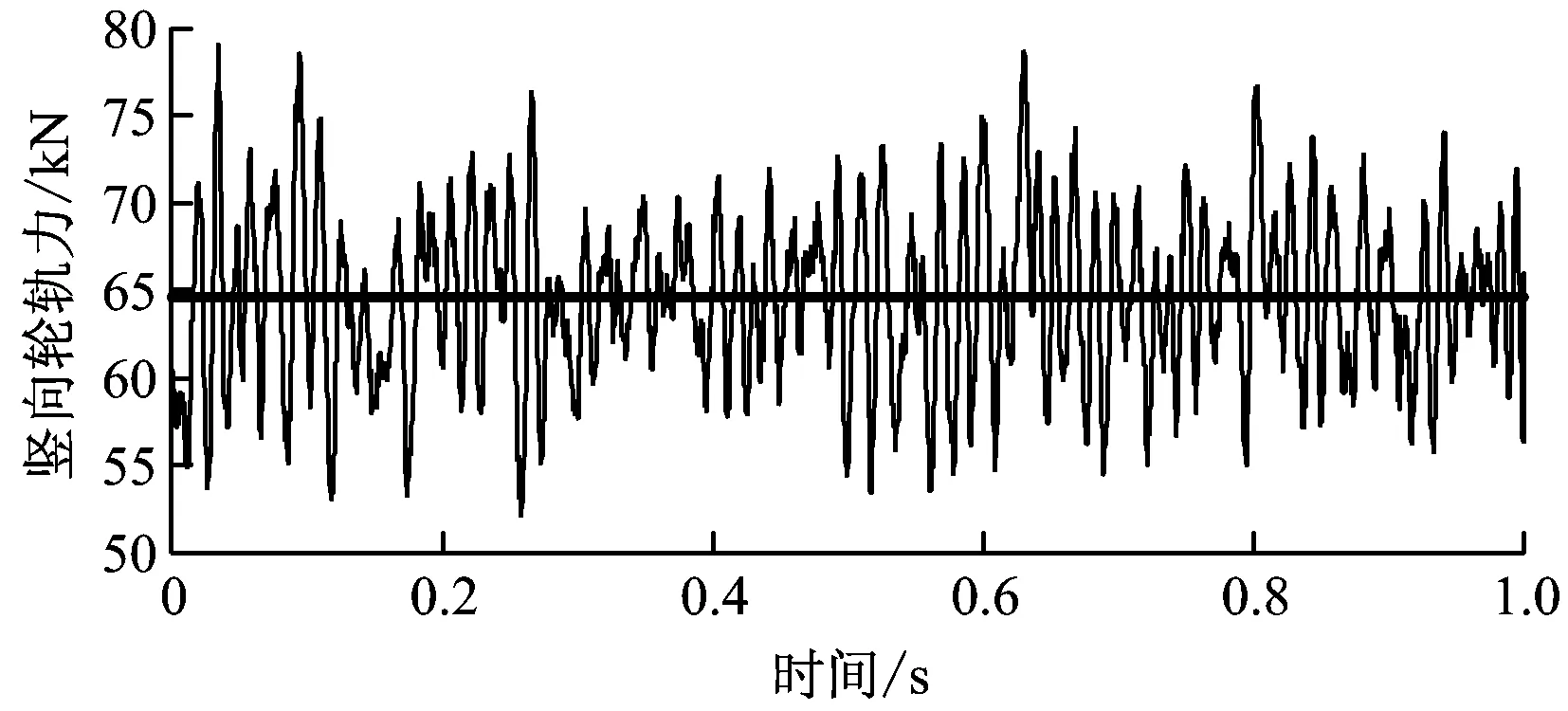
c) 本文模型计算结果图3 采用SIMPACK软件模型的验证对比

2.2 模型验证(2)

采用文献[7]提出的横向有限元与无砟轨道板段单元的车轨系统竖向振动分析法，进行算例比较。计算条件为高速列车(1动+4拖)以200 km/h速度在板式轨道上运行(根据1.1节中提出的梁与弹簧单元处理方法，建立了CRTS2型轨道板模型，即钢轨梁-扣件弹簧-轨道板梁-砂浆均布的弹簧模型)。取钢轨不平顺波长为12.5 m、波幅为3 mm的周期性正弦函数为轨道高低不平顺激振源，对两种方法的计算结果进行比较。采用本文算法计算结果如图4所示。

从图4可以看出，各响应波形符合物理概念，各项结果与文献[7]计算得到的系统动力响应幅值与变化规律基本一致，由此证明了本文算法及车辆-轨道简化模型的可行性。

a) 动车车体竖向加速度时程

b) 动车轮轨竖向力时程

c) 钢轨中点竖向位移时程

d) 轨道板竖向位移时程

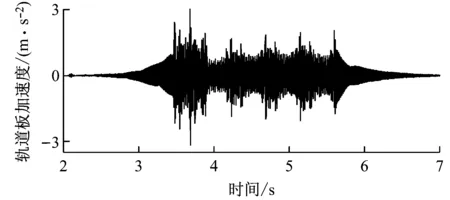
e) 轨道板竖向加速度时程图4 采用空间耦合模型的验证对比

3 算例分析

考虑单节整车模型，车速设为20 m/s。轨道模型及参数如1.1节所示，轨道长设为120 m(考虑两倍以上的最大不平顺波长及适当的边界)，同时引入轨道不平顺。选用瑞利(Rayleigh)阻尼，其中α=0.2、β=0.000 2。为使计算模型容易收敛，计算步长取钢轨有限元模型的网格尺寸除以车速的值，即1×10-4s。频谱分析重点考虑0～1 000 Hz频率范围内的振动。

3.1 上部子系统振动评价

计算得到的上部子系统振动结果包括了车厢、转向架和车轮振动加速度，其加速度级1/3倍频程的对比见图5。

a) 车厢竖向加速度

c) 车轮竖向加速度

d) 车辆部分加速度振级1/3倍频程对比图5 单节整车上部子系统振动计算结果

(1) 由图5可看出，轨道不平顺是引起车辆振动的主要原因。因一系、二系悬挂系统的减振作用使车厢振动得到很大衰减，舒适度指标为1.31，说明本文工况下车辆平稳性级别为优。

(2) 轨面平顺工况下，车轮加速度与轮轨力表现出类似的小幅度振荡，转向架与车厢加速度的这种表现依次减小。

(3) 由图5 d)可看出：车轮振动加速度分布在100 Hz以上，以中高频振动为主；转向架振动加速度分布在10～100 Hz范围内；车厢振动加速度主要分布在1～20 Hz范围内，以低频振动为主。另外，由于共振，车厢在2 Hz范围内的加速度振级衰减要小于其它频段。

3.2 下部子系统振动评价

通过计算可得到浮置板轨道下部子系统的钢轨、浮置板、隧道的位移及加速度时程曲线，以及轨道部分加速度振级1/3倍频程曲线。

(1) 由图6 a)可得，钢弹簧浮置板轨道由于支座刚度较小，钢轨及轨道板的竖向位移较大，钢轨最大竖向位移为3.23 mm、轨道板最大竖向位移为2.75 mm。《浮置板轨道技术规范》[8]对竖向位移规定为，钢轨的最大值为4 mm、浮置板的最大值为3 mm，由此可见本文位移指标均未超标。另外，隧道的竖向位移受轮对冲击作用要远远弱于钢轨和浮置板的作用。

(2) 由图6可看出，轨道不平顺也是引起轨道振动的主要诱因。时域上，车轮经过时钢轨加速度有明显的峰值，最大值为357 m/s2，是车厢最大振动加速度的3 000多倍；钢轨振动经过扣件的传递后，轨道板的振动已有衰减，其加速度最大值为14.19 m/s2；而隧道加速度最大值为0.027 m/s2，仅为钢轨最大加速度值的1/13 500，说明浮置板轨道减振效果显著。轨面平顺时，下部系统的振动主要表现为轮对对钢轨的冲击作用。

(3) 由图6 d)可看出，钢轨振动加速度分布在100 Hz以上，以中高频振动为主，这点与轮对类似；浮置板、隧道振动加速度同样分布在100 Hz以上，较浮置板加速度振级和隧道加速度振级有较大的降幅，最大相差约60 dB。

3.3 轨道不平顺波长的影响

为分析轨道不平顺波长对系统振动的影响，将不平顺波长划分为0.01～0.10 m、0.10～1.00 m、1.00～50.00 m、0.01～50.00 m及轨面平顺等5种工况，并延用上述模型及参数进行计算。对车辆部分，选用舒适度指标、转向架加速度、轮对加速度、轮轨力变化幅度等作为对比指标；对轨道部分，选用钢轨、浮置板、隧道的加速度及位移作为对比指标。

a) 下部子系统竖向位移

b) 跨中钢轨竖向加速度

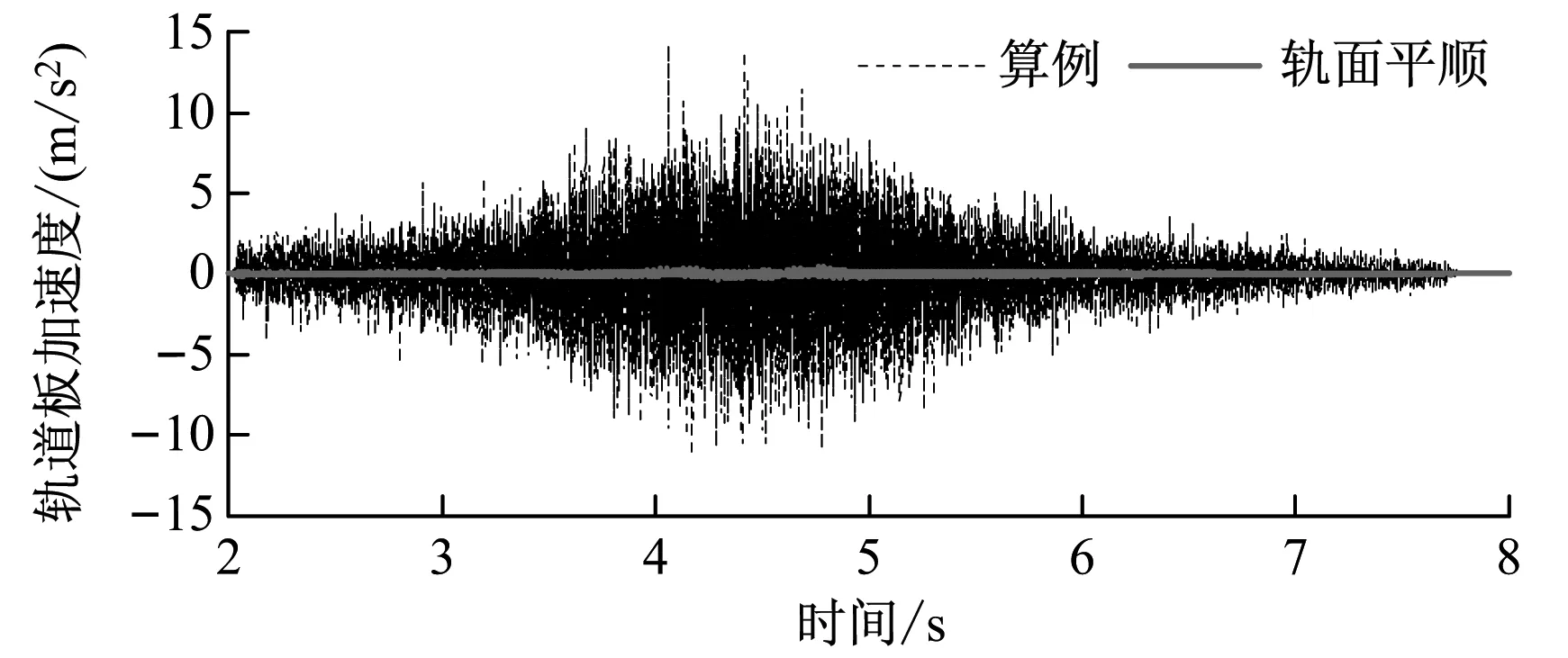
c) 跨中浮置板竖向加速度

d) 跨中隧道竖向加速度

e) 轨道部分加速度振级1/3倍频程对比图6 单节整车下部子系统振动计算结果

(1) 由表1可见，0.01～1.00 m范围的短波不平顺对车辆舒适性影响不大，特别是0.01～0.10 m波段的结果，与轨面平顺工况相近；0.01～0.10 m范围的短波不平顺对转向架加速度影响不大；轮对加速度受短波不平顺影响更大，其中0.10～1.00 m波段的影响大于0.01～0.10 m波段；轮轨力变化幅度表现与轮对加速度指标类似，1.00 m以上的波长对其影响较小。

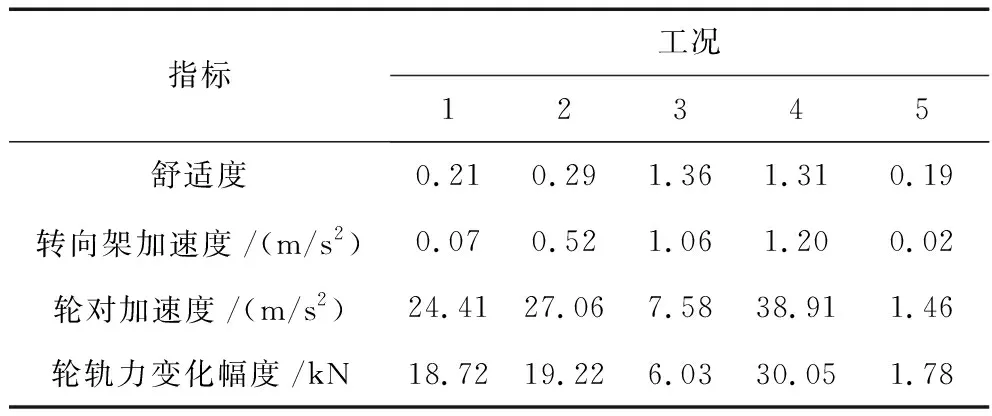
表1 5种不平顺工况下的上部子系统指标变化情况表

(2) 由图7可见，1.00～50.00 m波段与0.01～50.00 m波段的不平顺对车厢加速度振级影响相近，说明车厢振动受短波不平顺的影响较小；0.01～1.00 m波段不平顺在40～200 Hz左右对车厢加速度振级的影响要略高于0.01～0.10 m波段时的影响。

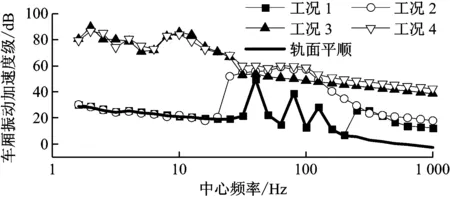
图7 不同工况下车厢加速度振级1/3倍频程对比

(3) 由图8可见，轨面平顺工况下，轮轨力受扣件影响主要表现在40 Hz和80 Hz两个主频；0.01～1.00 m波段对轮轨力的影响在频率200 Hz范围内与0.01～50.00 m波段相当，且主频均在100 Hz左右，可见钢轨有限元模型的网格应至少表征出0.10 m波长时的情况；0.01～0.10 m波段不平顺对轮轨力变化幅值影响弱于0.10～1.00 m波段，但诱发频率200 Hz以上的轮轨力产生变化；1.00～50.00 m波段对轮轨力影响相对较小。

图8 不同工况下轮轨力变化幅值1/3倍频程对比

(4) 由表2可知，钢轨加速度幅值主要受0.01～0.10 m不平顺波段的影响；对轨道板和隧道加速度幅值而言，0.01～0.10 m、0.10～1.00 m不平顺波段对其影响均较大，1.00～50.00 m不平顺波段对其影响较小；不平顺波长对轨道部分的位移影响不大。

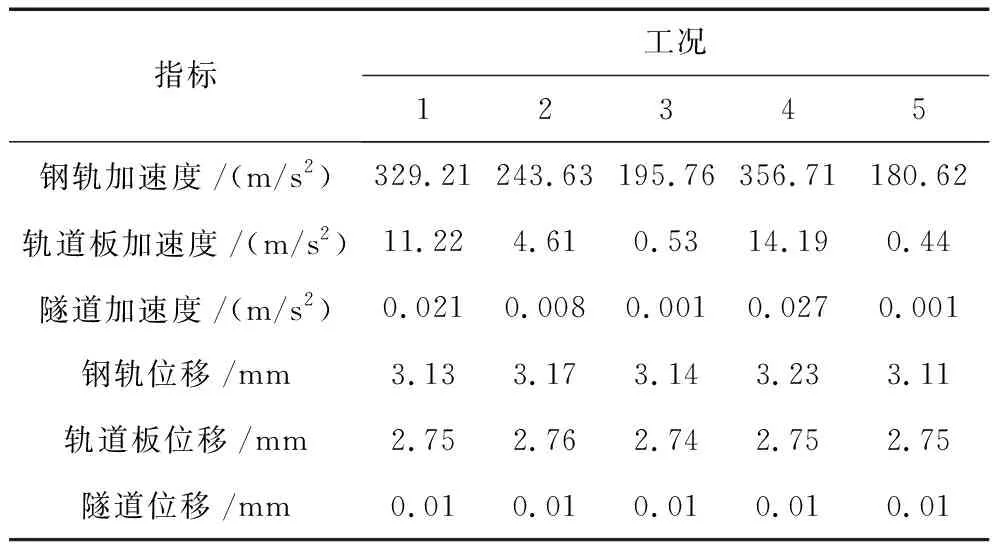
表2 5种不平顺工况下的下部子系统指标变化情况表

(5) 由图9可见，钢轨加速度以高频振动为主，主要影响波段在0.01～0.10 m，0.10～1.00 m不平顺波段对钢轨加速度的贡献分布在40～200 Hz范围内，40 Hz以内的钢轨加速度受不平顺波长影响较小；由于扣件的作用，轨道板加速度对于高频振动有所过滤，但仍以中高频为主；轨面平顺工况下，轨道板加速度受扣件的影响表现在40 Hz和80 Hz两个主频；与钢轨加速度不同，1.00～50.00 m不平顺波段对轨道板低频振动影响较大，0.01～0.10不平顺波段对其影响很小；振动传递至隧道后，加速度的各频段振级差进一步缩小，变化规律与轨道板加速度类似。

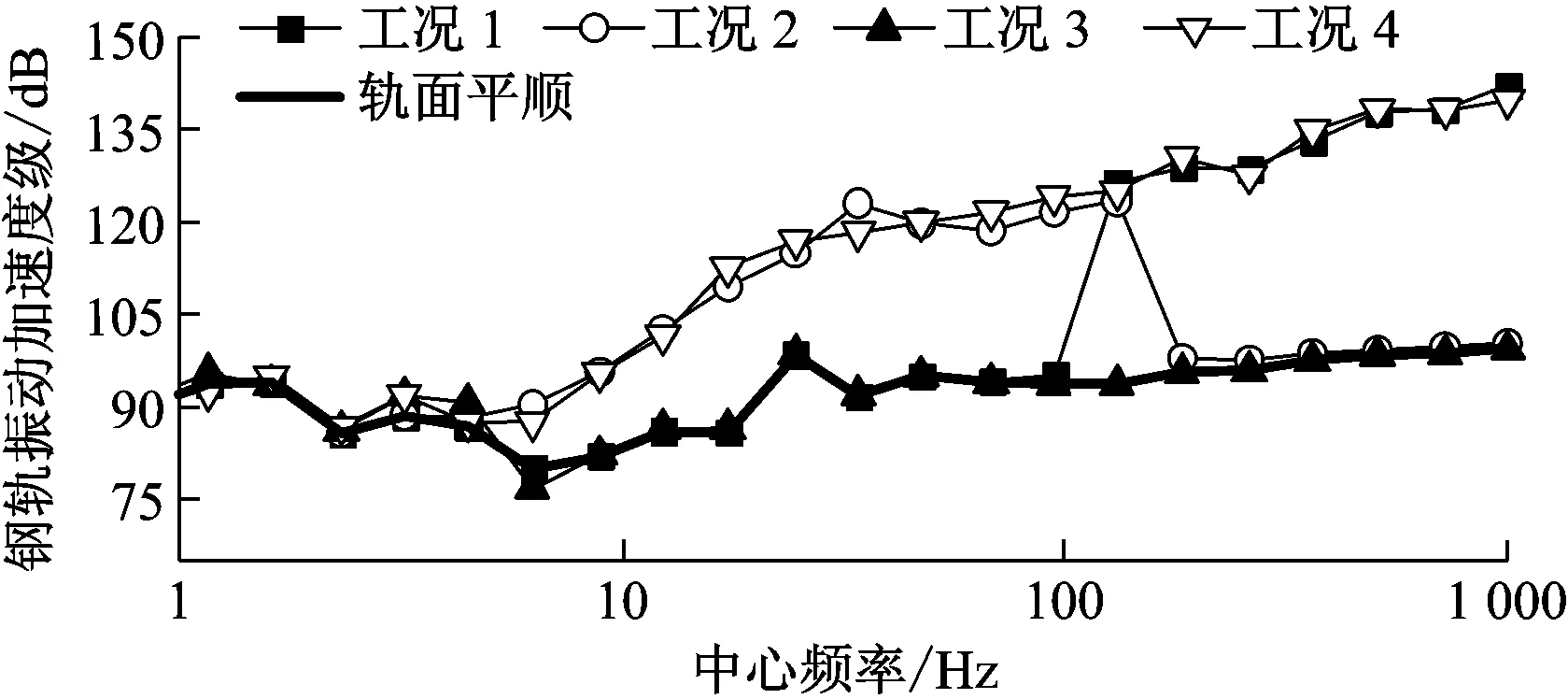
a) 钢轨加速度1/3倍频程对比

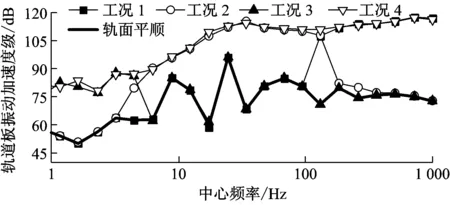
b) 浮置板加速度1/3倍频程对比

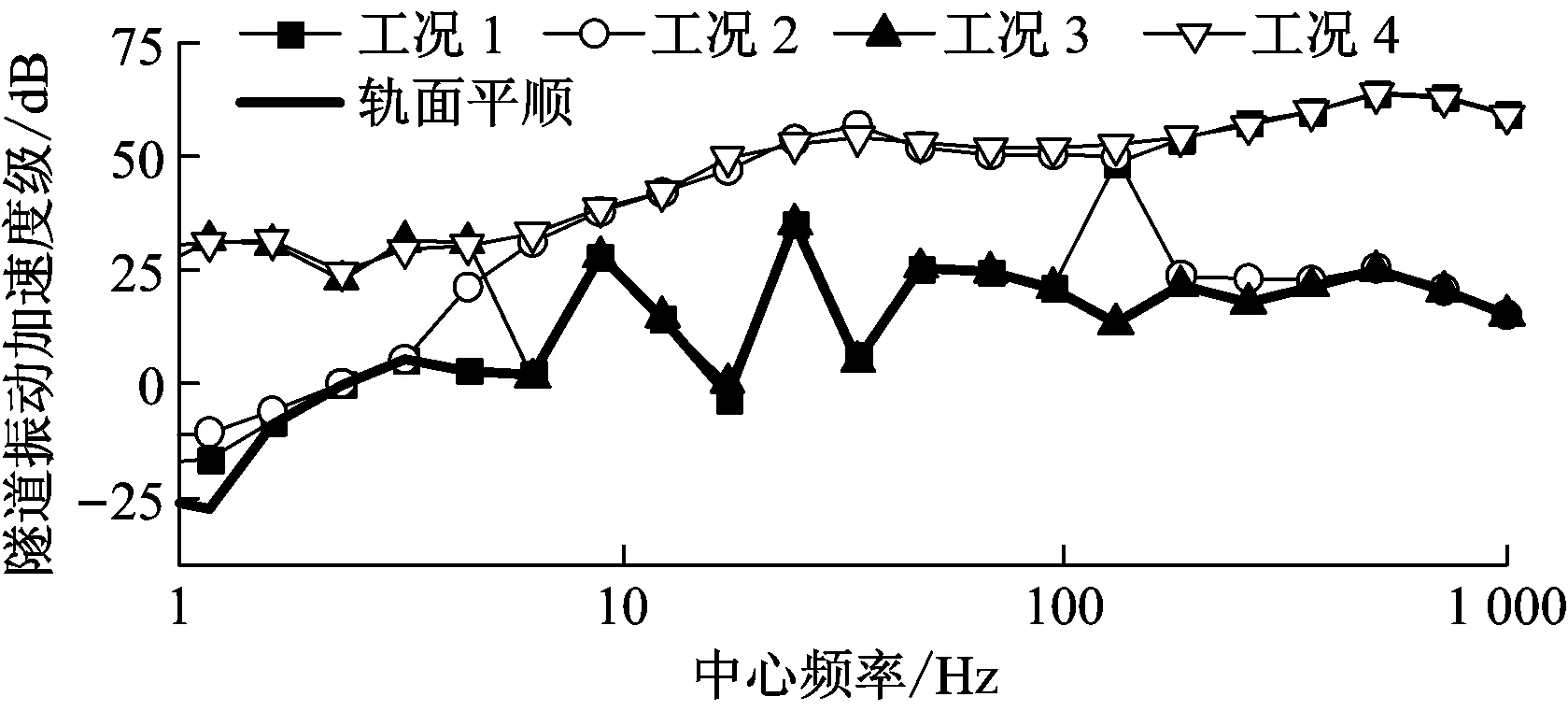
c) 隧道轨加速度1/3倍频程对比图9 轨道加速度振级频域对比

4 结论

本文提出了一种基于ABAQUS软件的二维车辆轨道-耦合动力学模型，该模型可以考虑轨道短波不平顺的影响。通过与SIMPACK软件和既有文献的建模型对比，验证了本文模型的正确性。此外，本文以地铁B型车-浮置板轨道为例，分析了车速在20 m/s时轨道不平顺波长对系统振动的影响，可得到以下结论：

(1) 轨道不平顺是诱发系统振动的主要原因。钢轨扣件对于高频振动有一定减振效果，在浮置板及钢弹簧支座的共同作用下，全频段减振效果显著，达60 dB。

(2) 车厢振动以低频振动为主(0～20 Hz)，由1.00～50.00 m波段的轨道不平顺诱发；轮对竖向振动和轮轨接触力以中高频为主，由0.01～1.00 m波段的轨道不平顺诱发；钢轨竖向振动以中高频为主，由0.01～0.10 m波段的轨道不平顺诱发。

(3) 研究对象为车厢振动时，钢轨有限元模型的纵向网格尺寸取0.1 m左右是合理的；研究对象为轮轨作用时，必须考虑短波不平顺(0.01～0.10 m)的影响，而本文模型可以在此波段更好地进行仿真。

(4) 地铁振动诱发的环境振动分布在100 Hz内。当考虑0.10～50.00 m轨道不平顺波段时，能够反映0～250 Hz频段内的振动，可见采用ABAQUS软件建立的车辆-轨道-大地空间模型中，钢轨有限元模型的纵向网格尺寸取0.1 m左右是合理的。