简支梁桥上CRTSⅠ型板式无砟轨道伸缩力影响因素分析*
雷振宇 张鹏飞 翟利华 农兴中
(1.广州地铁设计研究院有限公司,510010,广州;2.华东交通大学铁路环境振动与噪声教育工程研究中心,330013,南昌//第一作者,高级工程师)
我国高速铁路多采用以桥代路的方式来减小占地面积,桥梁结构形式多为预应力混凝土箱梁,桥上轨道结构多采用无砟轨道和跨区间无缝线路技术。桥上的无缝线路受力情况与路基上明显不同:混凝土梁体在自然环境中受温度荷载作用会发生伸缩变形,层间摩擦阻力带动底座板、CA砂浆、轨道板产生纵向变形及纵向力,轨道板通过扣件对钢轨施加纵向力并使其产生纵向变形及纵向力,该纵向作用力被称为附加伸缩力。
目前,国内外学者的研究主要倾向于温度荷载、制动荷载、列车荷载作用下桥上无砟轨道的静/动力特性及参数优化[1-8]。本文基于有限元法,建立了6×32 m简支梁桥上CRTSⅠ型板式无砟轨道无缝线路空间耦合模型,研究在温度荷载作用下,桥上无砟轨道无缝线路附加伸缩力分布规律,并对其影响参数进行了分析计算,为完善桥上无砟轨道无缝线路设计方法提供参考。
1 计算模型的建立
双线铁路6×32 m简支梁桥上CRTSⅠ型板式无砟轨道无缝线路力学模型示意图如图1所示。
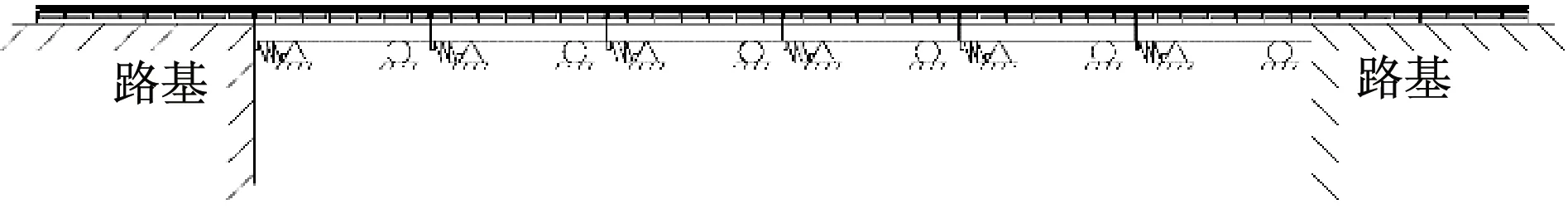
a) 整体

b) 局部图1 简支梁桥上CRTSⅠ型板式无砟轨道 无缝线路力学模型示意图
1.1 空间耦合模型
(1)采用铁摩辛柯梁,梁单元模拟CHN60标准钢轨,弹簧单元模拟WJ-7型扣件,扣件间距为0.629 m,全面考虑扣件系统对钢轨的纵、横、垂向约束。其中,横向和垂向刚度采用COMBIN 14弹簧-阻尼器单元模拟,横向和垂向刚度大小分别为50 kN/mm和35 kN/mm;纵向刚度采用COMBIN 39非线性弹簧单元模拟,纵向阻力取值按式(1)计算。单组扣件提供的最大纵向阻力为15.096 kN/组,取15 kN/组。

式中:
r——纵向阻力;
x——钢轨与轨道板之间的相对位移。
(2)轨道板和CA砂浆层采用实体单元模拟,轨道板为C60预应力混凝土结构。在32 m简支梁上设2块长为3 685 mm的梁端轨道板和5块长为4 962 mm的跨中轨道板,轨道板之间均设置70 mm的板缝。路基地段均采用长为4 962 mm的标准轨道板,轨道板宽度为2 400 mm,厚度为190 mm。砂浆充填层的长度和宽度与轨道板尺寸相同,厚度为50 mm,弹性模量取200 MPa。
(3)底座板和凸形挡台均为C40预应力混凝土结构,采用实体单元模拟。底座板宽为2.8 m,厚为200 mm。桥梁段每块底座板之间均设置20 mm的伸缩缝,和轨道板板缝相应对齐并绕过凸形挡台。在路基上,4块底座板纵向相连。凸形挡台为260 mm的圆柱或半圆柱结构,设计高度为450 mm。凸形挡台与轨道板之间填充的树脂材料厚度为40 mm,弹性模量为25 MPa,均采用实体单元模拟。
(4)预制箱梁为C50预应力混凝土结构,采用实体单元模拟,箱梁截面结构参数如图2所示。

图2 双线简支箱梁跨中截面
由以上各部分组成的6×32 m简支梁桥上CRTSⅠ型板式无砟轨道无缝线路空间耦合有限元模型如图3所示。桥梁两端分别建立了40 m的路基段,以消除边界效应。

图3 简支梁桥上CRTSⅠ型无砟轨道 无缝线路空间耦合模型
1.2 计算参数的选取
根据《铁路无缝线路设计规范》[9],混凝土梁年温差取30 ℃,双线简支梁桥墩顶纵向水平刚度取350 kN/cm,桥台顶纵向水平刚度取3 000 kN/cm。
2 梁体温差的影响
本节轨道板和底座板分别降温40 ℃和35 ℃,梁体按分别降温25 ℃、30 ℃和35 ℃3种工况考虑。不同梁体温差条件下的钢轨伸缩力、桥上轨道板及底座板纵向应力分别如图4—图6所示,其计算结果的最大值如表1所示。图表中,正值代表拉(应)力,负值代表压(应)力,下同。不同梁体温差条件下的钢轨纵向位移及轨板相对位移分别如图7和图8所示,其计算结果的最大值如表2所示。图表中,正值代表拉伸变形,负值代表压缩变形,下同。
从图4—图8、表1及表2可知,温度荷载作用下,钢轨伸缩力的峰值出现在桥梁墩台及跨中。由于桥上CRTSⅠ型板式无砟轨道底座板及轨道板的纵向不连续性,因此其纵向应力图成波动曲线,其中图线中的突变是由于板缝的存在,且凸形挡台在一定程度上分担了一部分底座板纵向应力的传递;随着梁体温差的增大,钢轨纵向力随之增大,但增幅不大;由于轨道板/底座板与梁体间温差的减小,其纵向应力随之减小,且减幅明显,这说明轨道板/底座板附加纵向应力主要来自于轨道与桥梁间的温差;钢轨纵向位移在桥梁跨中达到最大,在路基上逐渐减小至零;轨板相对位移在固定支座处较小,在活动支座处达到最大。
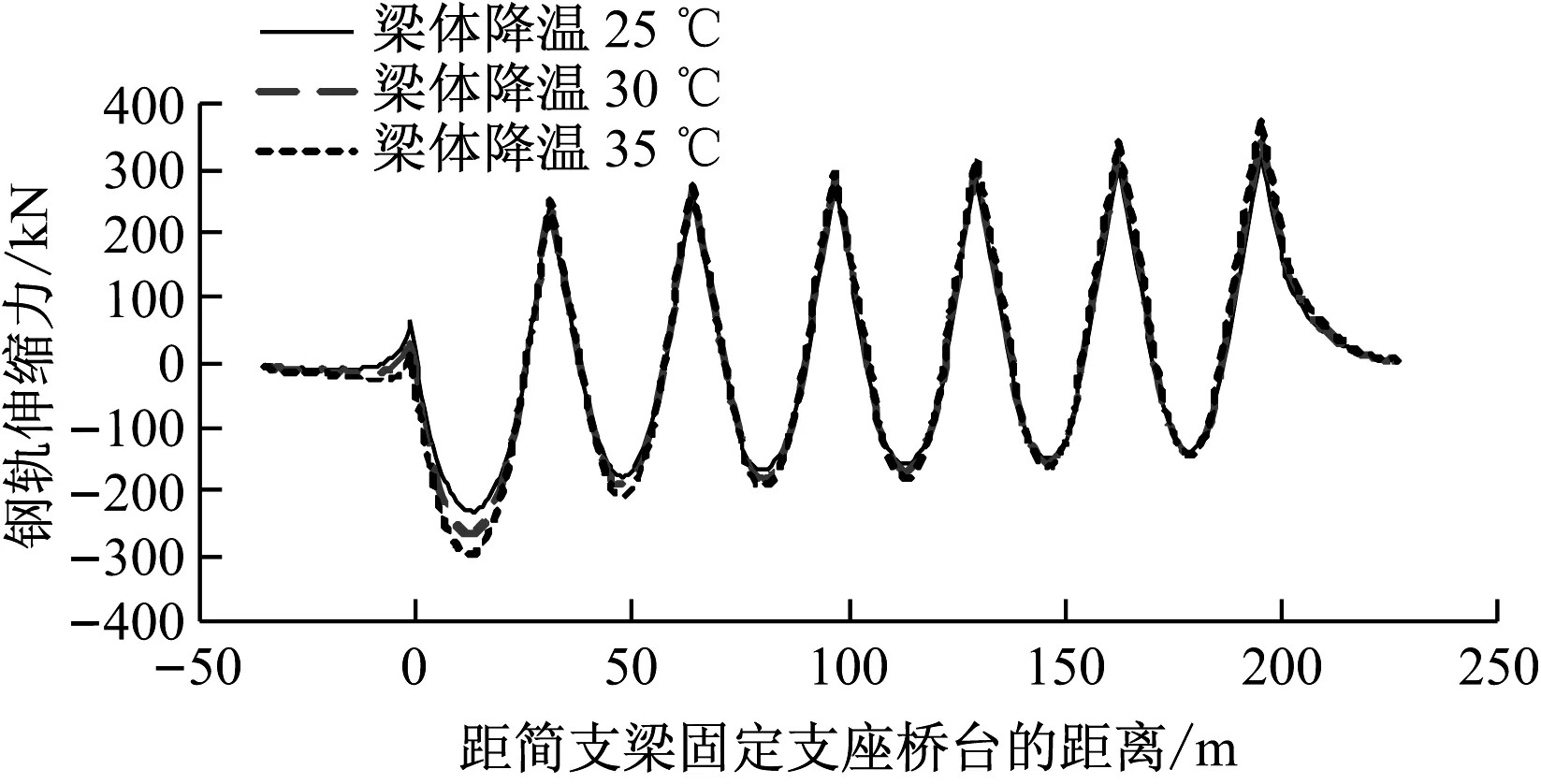
图4 钢轨伸缩力
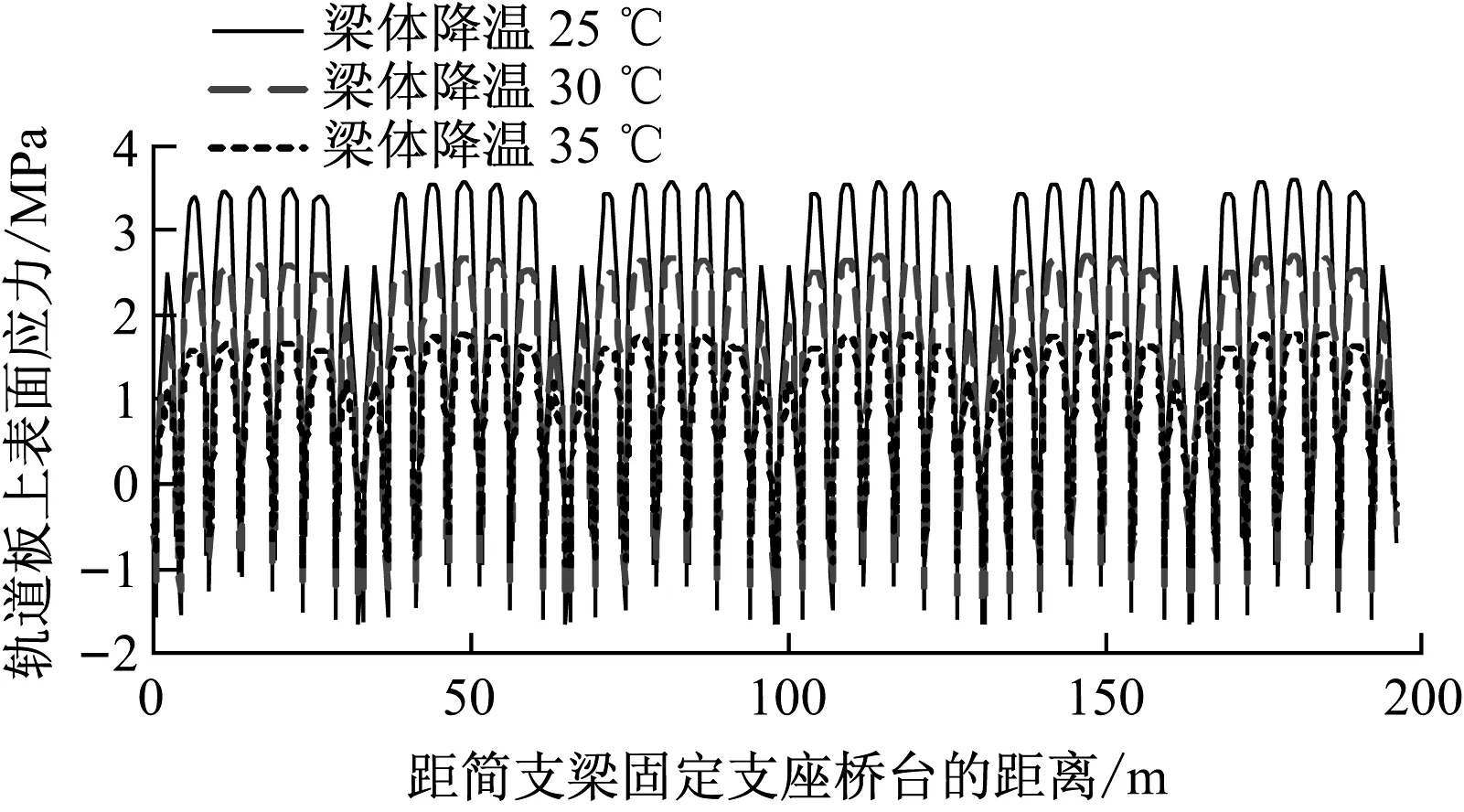
图5 桥上轨道板上表面纵向应力

图6 桥上底座板下表面纵向应力
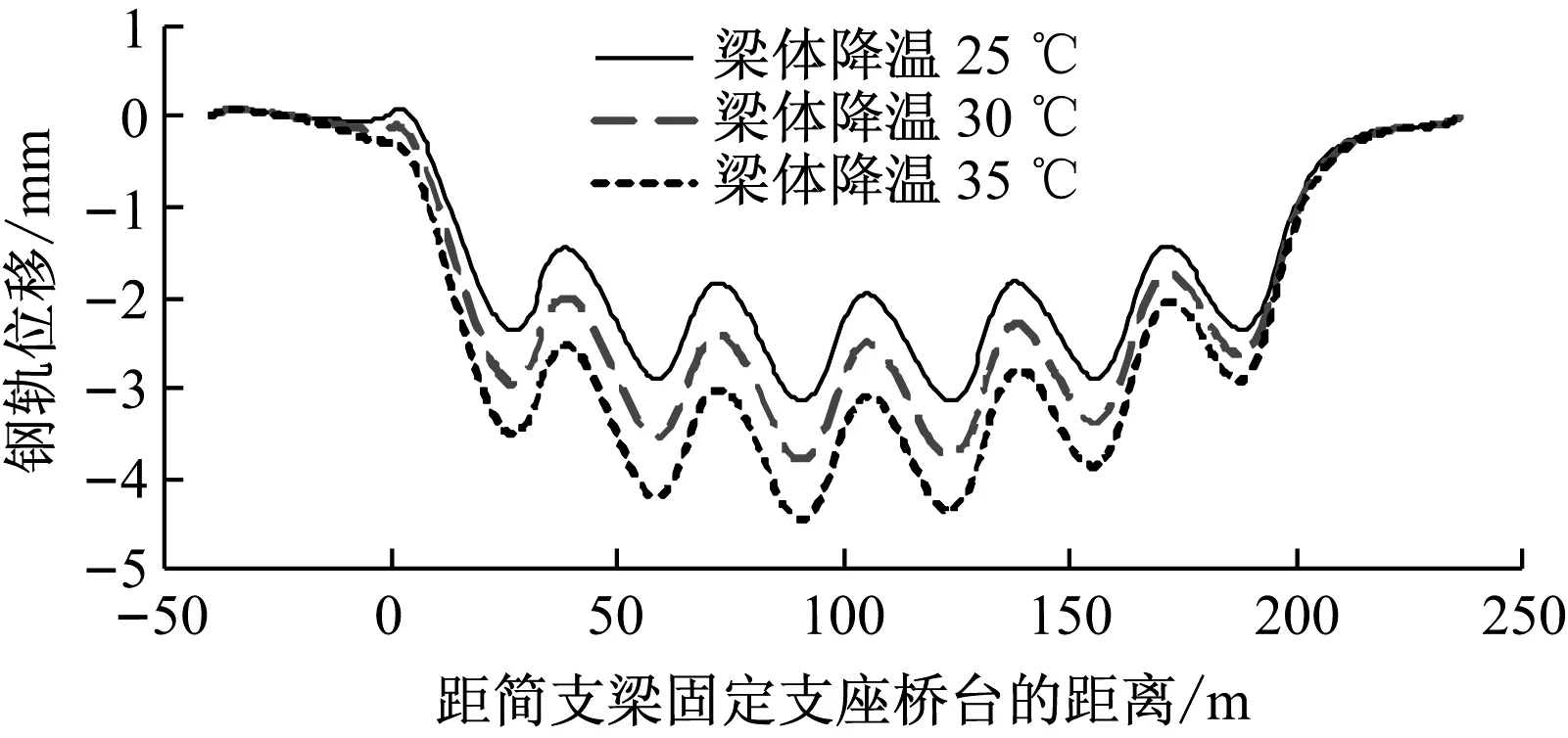
图7 钢轨纵向位移

图8 轨板相对位移表1 轨道结构纵向力最大值

梁体温差/℃钢轨伸缩力/kN轨道板上表面应力/MPa轨道板下表面应力/MPa底座板上表面应力/MPa底座板下表面应力/MPa正值负值正值负值正值负值正值负值正值负值25323.91231.143.611.684.161.871.415.6430351.12263.982.711.333.070.830.983.381.0835375.53296.211.810.991.970.471.161.102.79

表2 轨道结构纵向位移最大值 mm
梁体温差对桥上轨道结构纵向位移有较大影响,随着梁体温差的增大,桥上轨道结构纵向位移随之增大,且增量较大。因此,在昼夜温差较大的情况下,要加强对轨道结构的检测维护,以免钢轨承受过大的拉力,防止因轨板相对位移过大而导致扣件失效。
3 扣件纵向阻力的影响
本节桥上扣件纵向阻力分别按4 kN/组、10 kN/组、15 kN/组及20 kN/组4种工况考虑,不同扣件纵向阻力条件下的钢轨伸缩力、纵向位移及轨板相对位移分别如图9—图11所示,其计算结果的最大值如表3所示。
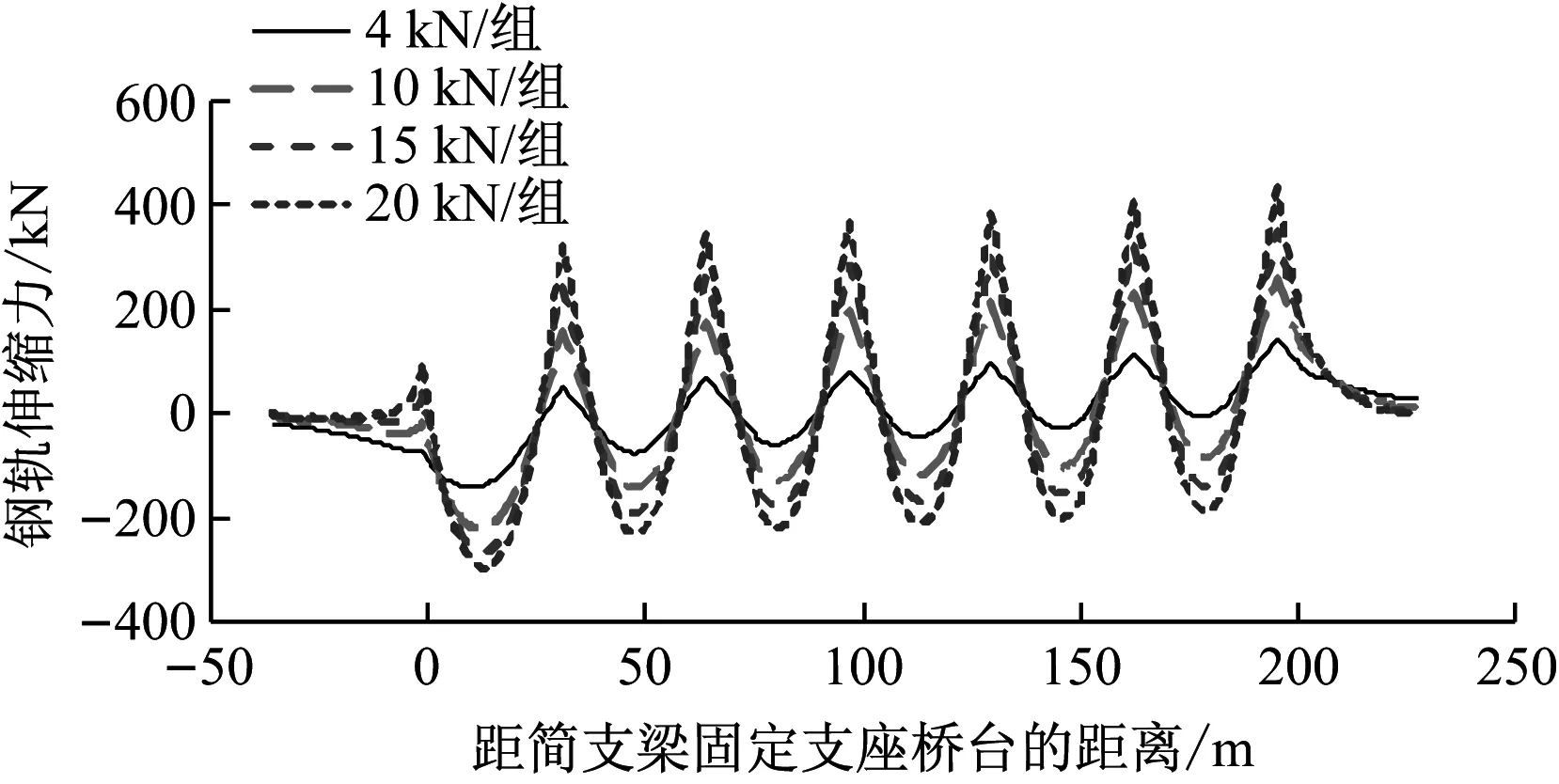
图9 钢轨伸缩力

图11 轨板相对位移
从图9—图11和表3可知,扣件纵向阻力对桥上轨道结构纵向力/位移有较大影响,随着扣件阻力的减小,轨道结构应力在纵向的变化趋于平缓,最大值随之减小。由此可见,采用小阻力扣件对桥上CRTSⅠ型板式无砟轨道的受力是有利的,但钢轨位移及轨板相对位移随着扣件纵向阻力的减小而增大。因此,采用小阻力扣件时,桥台活动支座端是轨道结构的薄弱环节,需加强监测,使钢轨在桥台处的爬行能够得到有效控制。

表3 轨道结构纵向力和纵向位移最大值
4 桥台顶纵向刚度的影响
本节桥墩顶纵向刚度取350 kN/cm,桥台顶纵向刚度分别按3 000 kN/cm、10 000 kN/cm和全约束3种工况考虑。不同桥墩台顶纵向刚度条件下的钢轨伸缩力、纵向位移及轨板相对位移最大值如表4所示。

表4 不同桥墩台顶纵向刚度条件下轨道结构纵向力和纵向位移最大值
从表4可知,固定支座桥台顶纵向刚度对桥上轨道结构纵向力和纵向位移在一定范围内影响较大;随着桥台固定端纵向刚度的增加,左侧路基段及第一跨桥上轨道结构受力明显增大,左侧路基段及前三跨桥上轨道结构纵向位移明显增大,对后三跨及右侧路基影响较小。由此可知,从减小钢轨伸缩力及纵向位移的角度考虑,桥台固定端纵向水平刚度不宜过大。
5 桥墩顶纵向刚度的影响
本节桥台顶纵向刚度取3 000 kN/cm,桥墩顶纵向刚度分别按200 kN/cm、350 kN/cm和500 kN/cm 3种工况考虑,不同桥墩台顶纵向刚度条件下的钢轨伸缩力、纵向位移及轨板相对位移如表5所示。
从表5可知,固定支座桥墩顶纵向刚度对桥上轨道结构纵向力影响不大,对纵向位移影响较大,但轨板相对位移变化不大;随着墩顶纵向水平刚度的增大,钢轨位移随之增大。因此,从减小钢轨纵向位移的角度考虑,墩顶纵向刚度不宜过大。

表5 不同桥墩台顶纵向刚度下轨道结构纵向力和纵向位移最大值
6 结论与建议
本文建立了多跨简支梁桥上CRTSⅠ型板式无砟轨道无缝线路空间耦合有限元模型,研究了温度荷载作用下钢轨、轨道板及底座板的受力变形特性,并对梁体温差、扣件纵向阻力、桥台固定端纵向刚度及桥墩固定端纵向刚度对伸缩力的影响进行了计算分析,得出以下几点结论:
(1)桥上轨道结构纵向位移随着梁体温差的增大而明显增大,在昼夜温差较大的情况下,要加强对轨道结构的检测和监测,以免活动支座墩顶处轨板相对位移过大而导致扣件失效。
(2)小阻力扣件可以起到降低轨道结构受力的作用,能改善桥上无缝线路梁轨相互作用;但当扣件阻力较小时,桥台处轨板相对位移会明显增大。因此,采用小阻力扣件时,桥台活动支座端是轨道结构的薄弱环节,需加强监测,使得钢轨在桥台处的爬行能够得到控制。
(3)固定支座桥梁墩台顶纵向刚度对桥上轨道结构纵向力和纵向位移在一定范围内影响较大,随着墩台顶纵向刚度的增大,钢轨伸缩力及位移随之增大,且增量明显。因此,从减小钢轨伸缩力及纵向位移考虑,桥梁墩台固定端纵向刚度不宜过大。

