基于概率断裂力学方法的钢吊车梁剩余疲劳寿命评估

郑军鹏

(中煤西安设计工程有限责任公司，陕西 西安 710054)

0 引言

近年来，通过对工业厂房调查发现，厂房中的重级和特重级钢吊车梁在吊车荷载的重复作用下会较早地出现不同程度的疲劳裂缝，危及生产安全，因此，研究和提出钢吊车梁剩余疲劳寿命评估方法具有重要的应用价值。

目前，国内外对结构或构件剩余疲劳寿命评估的方法主要有3种：传统疲劳寿命评估方法、基于断裂力学的疲劳寿命分析方法和基于损伤力学的评估方法。传统疲劳寿命评估方法主要是基于材料的S-N曲线和线性疲劳累积损伤理论。S-N曲线试验是用表面精心抛光的无任何宏观裂纹的光滑试件，而实际构件在加工及使用过程中，由于表面划痕、金属夹杂、腐蚀坑、锻造缺陷等等，构件表面往往存在各种类型的裂纹，所以，应用传统疲劳寿命评估方法所得到的结构疲劳寿命与结构的实际寿命存在一定的出入；损伤力学出现得比较晚，学术界对其还没有统一的认识，将其应用于工程实际还有很多工作要做。基于断裂力学的疲劳寿命分析方法承认结构构件初始缺陷的存在，更符合结构的实际情况，采用此法对在役结构剩余疲劳寿命的评估结果更加真实可靠。本文采用基于断裂力学的疲劳寿命分析方法对钢吊车梁剩余疲劳寿命进行评估。

1 基于概率断裂力学的剩余疲劳寿命评估

1.1 断裂力学理论

根据钢吊车梁的受力可知，钢吊车梁中的裂纹大多数为复合型裂纹。当实际裂纹是复合型裂纹时，往往作为Ⅰ型裂纹处理，这样更安全。因此，本文的研究以Ⅰ型裂纹为主。

构件的断裂起源于裂纹，而裂纹的静止、平衡或发展，都与裂纹尖端附近的应力场有直接关系，由线弹性理论得出裂纹尖端附近的应力场完全由应力强度因子KI来决定。应力强度因子通常表示为

(1)

式中：σ—名义应力；a—裂纹尺寸；α—形状系数(与裂纹大小、位置等有关)。

1.2 疲劳裂纹扩展

对于含有初始裂纹a0的构件，在承受交变应力时，初始裂纹a0会在交变应力作用下发生缓慢扩展，当扩展到临界值ac时，构件发生失稳破坏。从初始值a0扩展到临界值ac的过程叫做疲劳裂纹的亚临界扩展。

为了准确地描述疲劳裂纹扩展，通常用裂纹扩展速率来描述裂纹扩展的快慢。至今已提出了很多关于裂纹扩展速率的计算公式，其中在工程上应用最广的是Paris公式，Paris公式表示为

(2)

式中：C和m为疲劳裂纹扩展参数，这2个参数是与试验条件(环境、频率、温度等)有关的材料常数，ΔKI为应力强度因子幅度，ΔKI=KImax-KImin。

1.3 常幅应力下构件的剩余疲劳寿命估算

如果知道了构件的初始裂纹尺寸a0，临界裂纹尺寸ac，那么通过对Paris公式积分，就可以求得构件的剩余疲劳寿命。

由式(1)得

(3)

由于Δσ=σmax-σmin，

则式(3)表示为

(4)

则Paris公式可以表示为

(5)

式中：Δσ—应力脉，可以根据实测的应力-时间历程确定。

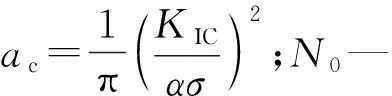
(6)

得到疲劳裂纹扩展寿命为

(7)

1.4 变幅应力下构件的剩余疲劳寿命估算

在实际工程中，构件受到常幅应力的情况很少，多数情况，构件承受的都是变幅应力。在变幅加载下，不同荷载循环间存在相互作用，所以载荷顺序影响着疲劳裂纹扩展寿命。通常，为了简单起见，不考虑荷载顺序的影响。Paris公式适用于常幅应力，变幅应力下不能直接使用公式(7)，通常先使用Miner准则将变幅应力转化为对应的等效常幅应力[1]，然后将等效常幅应力代入式(7)，求得构件的剩余疲劳寿命。变幅应力转化为等效常幅应力的公式为

则变幅应力下疲劳裂纹扩展寿命为

(8)

1.5 基于概率断裂力学的剩余疲劳寿命评估

采用线弹性断裂力学方法对结构的剩余疲劳寿命评估中，将其中的参数都当做确定性的量来考虑。但是，由于主观和客观因素的影响，这些参数都存在很大的不确定性，比如材料性能不确定性、外加荷载的随机性、裂纹形状简化当中的不确定性和无损检测所带来的裂纹尺寸的不确定性等。因此，就需要在断裂力学中引入概率统计的方法，将断裂力学和概率统计理论结合起来所形成的方法称为概率断裂力学。基于概率断裂力学的剩余疲劳寿命评估，是将随机参数看成具有一定统计分布的统计量来对结构剩余疲劳寿命进行评估的方法。

由式(8)知，变幅应力下，疲劳裂纹扩展寿命为

(9)

式(9)中共有6个参数，将这些参数都作为随机变量来考虑，那么，疲劳裂纹扩展寿命可以写成6个随机变量的函数，即

Nc=(C,m,α,Δσe,a0,ac)

(10)

通常，为了简单起见，在实际工程中将m和α取为常数(m=3,α=1)。那么，构件的疲劳裂纹扩展寿命评估公式中的自变量就只有4个。

对式(10)两边取对数，得

(11)

将上述各变量代入式(11)，可知构件的疲劳扩展寿命也服从对数正态分布，可以求出lgNc的均值μlgNc和标准差σlgNc。给定可靠度水平pr，可以查表得到upr(upr为与可靠度pr相关的“标准正态偏量”)，那么在此可靠度水平下的对数扩展寿命为

lgNc=μlgNc+uprσlgNc

(12)

Nc=10μlgNc+uprσlgNc

(13)

2 算例

2.1 基础参数

本算例的应力幅数据来自文献[3]。宝钢一炼钢原料跨、一浇铸跨、二浇铸跨28 m，21 m圆弧端吊车梁，吊车梁选用Q345钢，在使用了15年后的1999年，现场调查发现吊车梁圆弧端焊缝疲劳开裂；2002年，对钢吊车梁进行连续24小时的现场测试，经文献[3]统计发现Δσe服从对数正态分布，统计分析结果见表1。

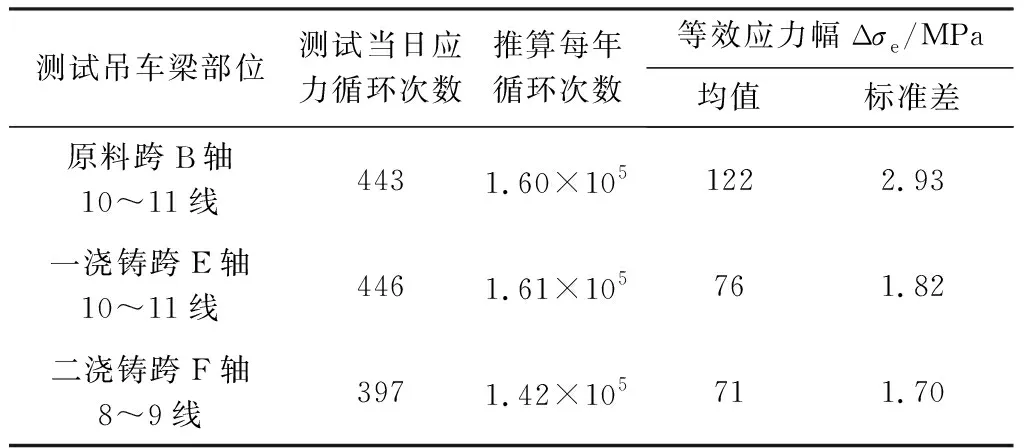
表1 吊车梁圆弧端动态应力幅实测结果

疲劳裂纹扩展参数C是与试验条件有关的材料常数。16Mn钢相当于Q345钢，因此参考文献[4]中对16Mn钢的统计结果，取lgC:(-11.811 7,0.256 662)。

文献[5]认为焊接接头含有的初始裂纹尺寸约为0.05～0.25 mm，本文取初始裂纹尺寸的最大值作为其均值，即μa0=0.25 mm，变异系数取δa0=0.5。

2.2 B轴10～11线钢吊车梁剩余疲劳寿命

由概率论知，对数正态分布与正态分布的关系是：设Y:N(μ,σ2)，令Y=lgX，则X就服从对数正态分布。对数正态分布和正态分布之间统计参数的转换关系为

(14)

(15)

式中：μlgX，σlgX—X对数的均值和方差；μX，σX—X的均值和方差；δX—X的变异系数。

求a0对数的统计参数：初始裂纹长度的均值和变异系数为μa0=0.25mm，δa0=0.5。由式(14)和(15)求得a0对数的均值和方差为

则lga0:N(-0.650 5,0.042 1)。

求Δσe对数的统计参数：原料跨B轴10～11线等效应力幅Δσe的均值和方差为μΔσe=122，σΔσe=2.93，Δσe的变异系数为

将μΔσe和δΔσe代入式(14)和(15)，求得Δσe对数的均值和方差为

则lgΔσe：N(2.086 2,1.085 9×10-4)。

不同可靠度下钢吊车梁的剩余疲劳寿命：由式(10)和(11)得到lgNc的统计参数为

(16)

(17)

将lgC，lga0和lgΔδe服从的统计参数代入上面2式得

μlgNc=-0.444 7+11.811 7-3×2.086 2+0.5×0.650 5=5.343 7

对于给定的可靠度pr，通过式(13)可求得钢吊车梁的剩余疲劳寿命。

(1)当pr=0.999时，upr=-3.091

则Nc=30 465次

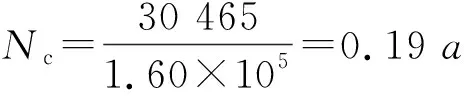
(2)当pr=0.99时，upr=-2.326

则Nc=49 728次

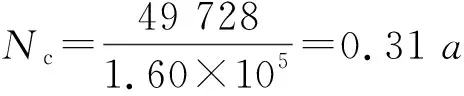
(3)当pr=0.95时，upr=-1.645

则Nc=76 913次

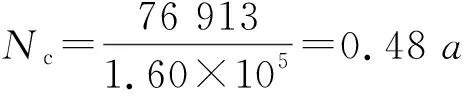
(4)当pr=0.9时，upr=-1.288

则Nc=96 694次

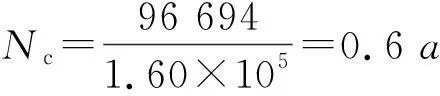
将在不同可靠度pr下所求的原料跨B轴10～11线钢吊车梁剩余疲劳寿命见表2。

表2 不同可靠度pr下原料跨B轴10～11线钢吊车梁剩余疲劳寿命

2.3 另外两线钢吊车梁剩余疲劳寿命

一浇铸跨E轴10～11线和二浇铸跨F轴8～9线钢吊车梁剩余疲劳寿命的求解过程与原料跨相同，将其列于表3和表4。

表3 不同可靠度pr下一浇铸跨E轴10～11线钢吊车梁剩余疲劳寿命

表4 不同可靠度pr下二浇铸跨F轴8～9线钢吊车梁剩余疲劳寿命

2.4 估算结果分析

通过概率断裂力学方法钢吊车梁剩余疲劳寿命评估中看出，随着可靠度的提高，剩余疲劳寿命减小。

采用概率断裂力学方法估算出宝钢一炼钢原料跨B轴10～11线、一浇铸跨E轴10～11线和二浇铸跨F轴8～9线钢吊车梁在可靠度为0.9时的剩余疲劳寿命分别为0.6 a、3 a和4 a。对宝钢一炼钢调查发现，浇铸跨B轴钢吊车梁圆弧端的疲劳裂缝最严重，E、F轴的疲劳破坏比B轴小一些。用概率断裂力学对这三跨吊车梁剩余疲劳寿命的评估结果与吊车梁的实际破坏情况比较吻合，这表明可采用概率断裂力学对钢吊车梁剩余疲劳寿命进行评估。

3 结语

鉴于传统疲劳寿命评估方法的缺陷，本文引入概率断裂力学的方法对钢吊车梁的剩余疲劳寿命进行评估，并通过算例进行验证，表明采用概率断裂力学方法能够对钢吊车梁的剩余疲劳寿命进行评估，结果更符合实际。