利用超限学习算法计算致密砂岩储层渗透率方法研究

刘旭辉

中国石油集团测井有限公司生产测井中心，陕西 西安

1.引言

随着勘探开发的进行，致密砂岩储层逐渐变为了主力储层，针对致密砂岩储层的精细研究具有十分重要的意义[1][2][3][4]。致密砂岩存在孔隙类型多样、孔隙结构复杂的特点，导致其流体渗流十分复杂，储层渗透率变化较大，常需要进行针对性的压裂改造[5][6][7][8]。所以，准确计算致密砂岩储层渗透率至关重要[9][10][11][12][13]。

在地层中取出岩心并进行化验，可得到地层真实渗透率。但取心成本过高，制约了该方法的适用性，且无法进行连续取心。由于测井曲线可以连续测量径向地层特征，常被选为确定致密砂岩储层径向渗透率的替代方法。现有利用测井曲线评价渗透率的方法主要有4类：①利用测井曲线计算出孔隙度曲线，并利用孔隙度与渗透率的统计关系计算渗透率[14][15]；②利用测井曲线直接进行一元或多元回归计算渗透率[16][17]；③利用非常规测井(核磁共振测井、阵列声波测井、电成像测井)进行渗透率解释[18][19]；④通过人工智能算法与测井曲线相结合，进行非线性回归计算渗透率[20]。第①类方法中，虽然岩心孔隙度与岩心渗透率具有一定的相关性，但致密砂岩储层的孔隙度计算本身就存在一定难度，利用计算得到的孔隙度进行渗透率预测会产生二次传导误差，使渗透率预测精度降低；第②类方法中，由于致密砂岩储层的渗透率受各种因素综合影响，导致其与测井曲线具有较为复杂的非线性关系，利用普通的一元或多元线性回归算法难以准确表征致密砂岩储层渗透率变化；第③类方法由于测量了更多的储层信息，利用非常规测井进行储层渗透率评价可大大提高致密砂岩储层渗透率的计算精度，但非常规测井的测量成本较高，使其适用性大大减低；第④类方法结合了人工智能算法，与测井曲线进行非线性回归，建立了测井曲线与渗透率之间的非线性关系，利用该关系对整口井进行渗透率预测。上述4类方法中，第④类方法更适用于致密砂岩储层，但是现有的 BP神经网络等算法存在不适用于小样本、算法训练时间过长等缺点。基于上述问题，笔者提出了利用超限学习算法计算致密砂岩储层渗透率的方法。

2.超限学习算法

针对传统BP神经网络算法训练速度过慢、不稳定、不适应于小样本的缺点，Huang等[21][22]提出了一种速度极快的单隐层神经网络算法——超限学习算法。Huang提出，只要激励函数在任意区间上无限可微，那么权值及阈值就可以根据任意连续的概率分布随机生成，即神经网络无需对权值及阈值进行调整；又假设函数预测值与目标值以一定概率成立，即不需要输出层的偏置，则可得到一种新的单隐藏层神经网络——超限学习算法(图1)。

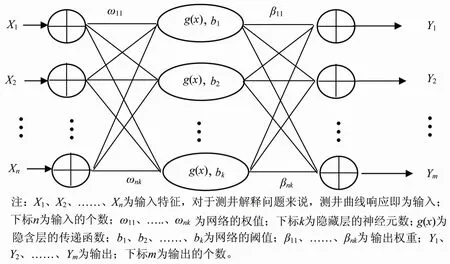
Figure 1.The extreme learning algorithm图1.超限学习算法

超限学习算法在输出层不存在偏置，而输入权重以及隐藏层偏置是随机产生的，并不需要调整，所以网络中仅剩下输出权重一项是没有确定的。首先，根据阿尔奇公式设定目标函数为：

式中：T为输出矩阵；H为输入矩阵；β为输出权重。

计算出式(1)的解即可完成网络构建。由超限学习算法的理论可知，当隐藏神经元个数(L)与训练样本的个数(N)相同时，H为可逆矩阵，则β可使神经网络以0误差拟合映射函数。但在实际情况中，L过大会使得模型泛化能力大大降低，若L远小于N时，应求取损失函数的最小值：

依据极小范数准则，式(2)存在极小范数最小二乘解：

式中：为隐藏层响应矩阵的Moore-Penrose逆。

根据岭回归原理，在加入正则化参数后，模型的泛化能力会增加。有：

式中：C为正则化参数；I为对角矩阵。

在计算出后，即可计算出β，并对新样本进行预测。

3.模型超参数确定

利用研究区致密砂岩储层2口井共57块岩样进行模型的训练及预测，其中47块岩样来源于A井，另外10块岩样来源于B井。选用常规测井曲线中的自然伽马曲线、密度曲线、中子曲线、声波曲线、电阻率曲线、光电吸收截面指数曲线作为输入曲线，渗透率曲线作为输出曲线。由于渗透率参数的变化范围过大，所以在实际计算时，需要对渗透率进行合理的归一化：

式中：K为渗透率；K′为对数下的渗透率；K′为对数后归一化后的渗透率；为对数下渗透率最低值；为对数下渗透率最高值。

在进行储层预测之前，需要确定模型中的参数，以得到最佳的预测结果。选用A井10块样本数据，进行模型中的正则化参数(C)与核参数(γ)的确定。由于样本数量较少，选用留一法对模型参数进行确定。留一法是将N个样本划分成N个样本集，每个样本集中具有N−1个训练样本以及1个预测样本；用N−1个样本进行建模，剩下的1个样本进行预测；再将某一超参数组合中的预测总误差除以N，则可得到留一法预测误差；最后误差最小的结果所对应的参数即为最佳超参数。留一法确定模型的误差曲面见图2。

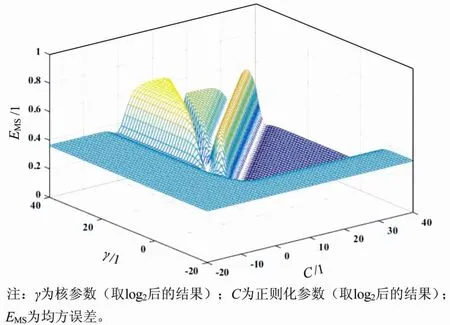
Figure 2.The diagrammatic sketch of error surface of leave-one-out model图2.留一法计算模型误差曲面示意图

从图2中可以看出，当模型的C与γ均大于1时，模型的误差开始减小，并且误差曲面会产生一定的波动。通过网格寻优的方法，确定模型的最佳超参数分别为：C为220，γ为227。

4.实例分析

利用上文得到的最优超参数，结合研究区的47块样本，以自然伽马曲线、密度曲线、中子曲线、声波曲线，电阻率曲线、光电吸收截面指数曲线的响应作为模型的输入，对应深度的岩心渗透率作为模型的输出。在建立模型后，利用模型对B井进行整口井渗透率的评价，对应的预测结果如图3所示。

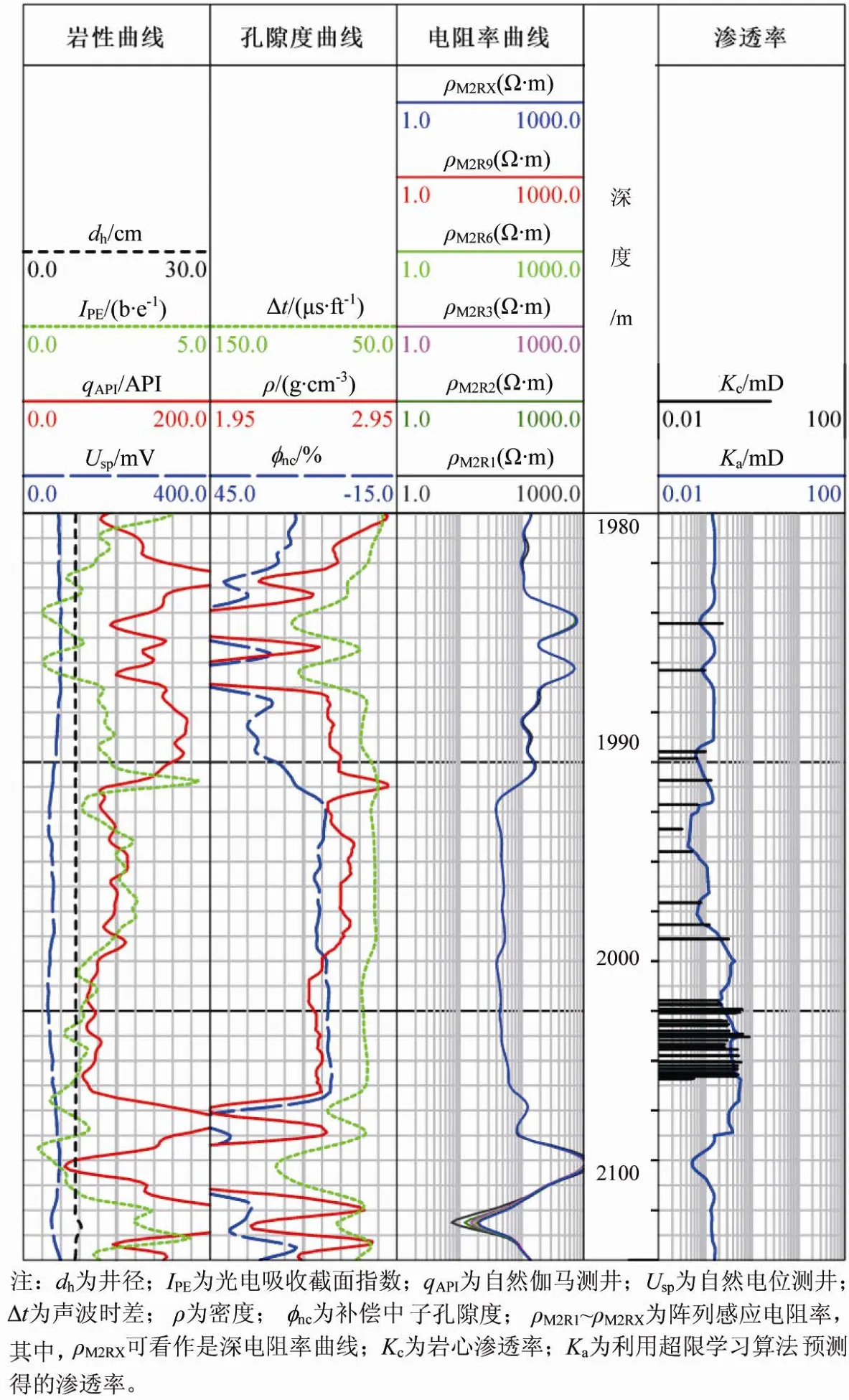
Figure 3.The diagrammatic sketch of logging interpretation of Well B图3.B井测井解释结果示意图

从图3可见，虽然常规测井曲线与渗透率的相关性不高，但超限学习算法却能较为准确地计算出致密砂岩储层的渗透率。值得一提的是，在模型建立时，超限学习算法的训练速度十分迅速，仅需0.0004 s，极适合于测井解释方面的问题。

5.结语

致密砂岩储层的渗透率是决定产能的重要参数之一，但致密砂岩储层的渗透率难以计算。超限学习算法是一种很有潜力的算法，可有效确定致密砂岩储层的渗透率，其预测精度高、训练速度快，更适合于测井解释问题。