助力减速机的动力合成与运行特性研究

张政泼， 董中新， 蒋桂平， 赖显渺， 黄桂云

（1.桂林航天工业学院机械工程学院，广西桂林541004；2.桂林广陆数字测控有限公司，广西桂林541213）

0 引言

助力减速机主要应用于我国和欧美国家鼓励推行、大力发展的电动助力自行车上[1-2]，是其核心部件。到目前为止，有关助力车的研究大多是针对控制系统方面的[3-7]，而关于助力车和助力减速机的整体特性研究资料还较少。同时，以往的助力控制模式主要强调电动机输出要与脚踏瞬时力矩实时满足大约1:1的特定比率关系[6-7]，并且助力模式下的电动机助力始终伴随着骑行运动。这一模式体现了一定的合理性，但其合成力矩波动性没有得到改善，且由于骑行者体力状况各异和变化，其效果并不一定能达到人们的期望，且在阻力较小时仍持续助力显然是浪费电能的。因此，本文提出和研究一种可改善上述问题的新助力模式。本文主要是针对助力减速机的力矩波动性及其合成特性，以及新助力模式的力学和运行特性进行分析研究。

1 助力减速机结构和新助力模式特点

1.1 助力减速机结构形式特点

助力减速机是脚踏驱动和电动机驱动的动力合成与输出装置，主要由脚踏机构、直流电动机、减速与超越机构、传感装置、控制器等部分组成，集成于较小的箱体内。其中，减速与超越机构由齿轮减速机构和2组超越离合器组成；传感部分由脚踏力矩和转速传感机构组成。图1为一般助力车及助力减速机传动原理图，脚踏机构和电动机均通过超越离合器与中置链轮相连，因此不会发生运动干涉；电动机至中置链轮设置了减速机构，实现转矩放大和利于应用电动机特性较好的高速段；中置链轮和后链轮之间可设置变速机构。图2为减速机工作原理框图。也有一些厂家和研究者取消了力矩传感功能，而是通过转速传感信号和特定助力程序实现助力控制[8]；也有研究者采用了电液驱动助力形式[9]，但结构相对复杂。助力减速机的布置主要有两种形式[10-11]：1）轮毂形式。即减速机置于轮毂上。2）中置式。为后期发展起来，即减速机与脚踏、链轮结合于中部。本文主要针对具有力矩传感功能的电动机助力模式以及中置式进行分析讨论，其原理和结果同样适合于轮毂式。

1.2 新助力模式特点

1）设定脚踏力矩的上设定值和下设定值，分别对应电动机助力的启动和停止信号阈值。2）采用脚踏等效力矩作为跟踪助力对比值，且电动机助力脚踏力矩下降至下设定值，则关闭电动机助力。本模式避免了阻力较小时仍然持续助力而浪费电能的现象，并在进入助力过程后具有一个合适的最小助力区间，以及在行驶过程具有更多的适应实际状况的选择调整方式，并且合成力矩波动性减小。

2 助力状态下的动力合成与力学特性分析

2.1 脚踏力矩的波动性质

1）脚踏力矩的波动表达式。

在实际骑行时，即使进入相对稳定状态，脚踏动力也是周期性波动的。一般脚踏运动在经过上下死点时具有提拉动作，加上双腿的交替用力和惯性作用，因而在经过上下死点时也施加着相当的力矩[12]。相对稳定时，对曲柄的踏蹬力矩可近似为正弦波变化[13-15]，周期为π（如图3），脚踏力矩的波动表达式为：

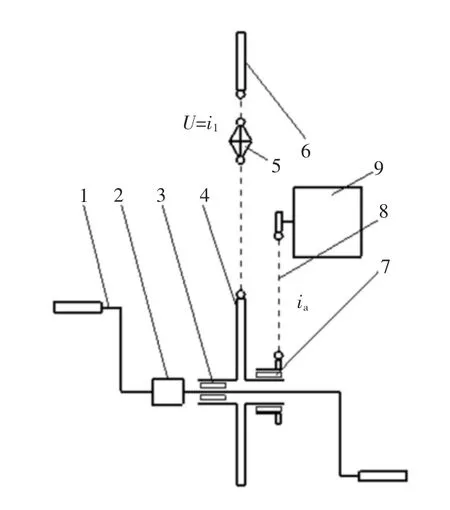
图1 助力减速机传动原理图

式中:Mt为脚踏力矩瞬时值；Mtmax为脚踏力矩峰值；Mtmin为

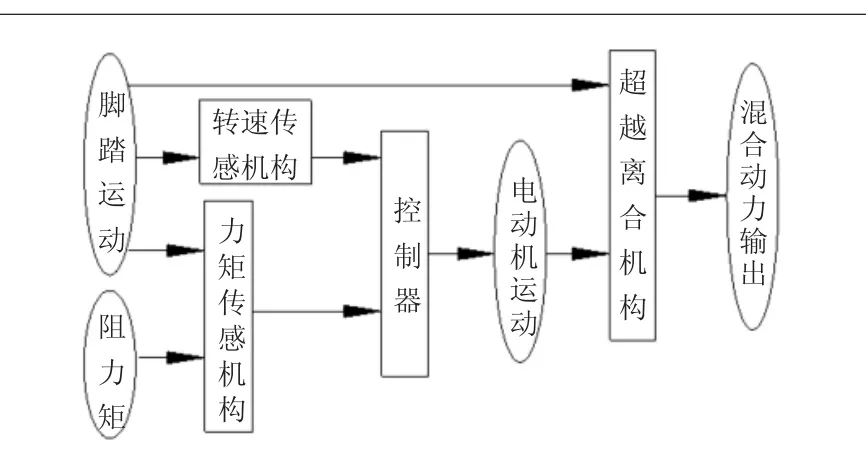
图2 助力减速机作用原理框图

脚踏力矩谷值；Mtp为脚踏力矩平均值；Mta为脚踏力矩波动振幅；φ为曲柄角度，并设曲柄处在接近竖直方向的死点位置时为0°。

2）相对波动系数及其特性。

定义“相对波动系数”：力矩幅值与其平均值之比。显然，相对波动系数可以有效表征该变化力矩相对于整体力矩水平的波动程度，定义式为

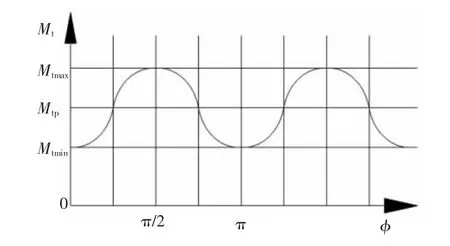
图3 脚踏力矩波动示意图

式中，τt为脚踏力矩的相对波动系数。τt值越大，说明力矩的相对波动程度越大，其导致的加速度和速度相对波动性越大。在稳定骑行状态下，整体脚踏速度是相对平滑稳定的[12]，实际上就是其相对波动系数τt值较小和惯性较大共同作用的结果。

在式（2）中，当波动幅值Mta为0，则τt值为0；当Mta为一定值，则Mtp越大τt越小，当Mtp→∞，则τt值为0；如Mtp为一定值，则Mta越大τt越大。也由此说明，以上定义的相对波动系数符合实际变化特性。

2.2 脚踏动力的等效形式

在旋转一个周期内，瞬时脚踏力矩值始终在变化，为了控制简便和降低合成力矩波动性，可采用等效力矩作为监测和跟踪助力对比量。按照曲柄旋转一周做功相等的等效原则，等效方程为

式中，Mtd为脚踏力矩等效值。将式（1）代入，得

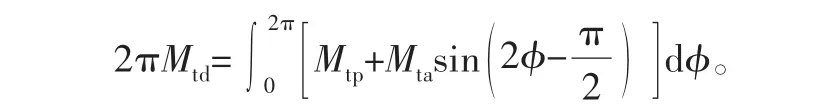
解之得Mtd=Mtp。

2.3 动力合成分析

动力合成有多种形式[16]，对于助力减速机，当进入电动机助力状态后，通过速度传感检测跟踪和控制，使电动机输出传动至中置链轮的角速度与脚踏角速度相同，确保速度同步；脚踏力矩与电动机力矩通过各自的超越离合器机构同时作用于中置链轮，因此属于并联传动、力矩合成类型。另外，超越离合器的传动效率是小于1的[17]，为讨论方便，同时也不影响一般分析，两种超越离合器的效率系数按较小值取。如图4，动力合成与力学关系式为

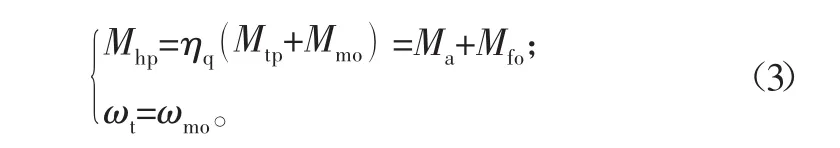
式中：Mhp为等效合成力矩；Mmo为电动机输出转换至超越离合器处的力矩，简称电动机转换力矩；ωt为脚踏角速度；ωmo为电动机传动至中置链轮处的角速度；ηq为离合器效率；Ma为对应加速运动的作用在链轮处的惯性力矩；Mfo为行驶阻力转换至中链轮处的转换阻力矩。由于Mtp是脚踏运动一个周期的平均值，需经过检测计算而确定，因此根据控制方式，Mmo相对于理论相位滞后一个周期π，这在Mtp有明显波动时会出现滞后特性，但在Mtp相对稳定时是基本没有影响的。

根据结构和传动特点存在下述关系：

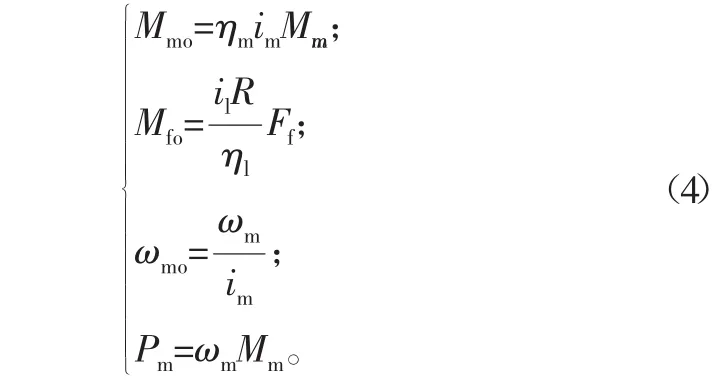
式中:Mm、Pm、ωm分别为电动机输出力矩、功率、角速度；ηm、im分别为电动机轴至离合器输入端的传动效率、减速比；R为轮毂半径；il、ηl分别为中链轮至后轮轴的增速比、传动效 率 ；Ff为 行 驶 阻力，即使进入平稳阶段后，Ff也具有一定的波动性，在此忽略其影响。

脚踏力矩与电动机力矩混合后，一般经历加速阶段，趋于相对平稳运行状态，除非再次改变骑行速度或遇到明显路况变化。后面的分析将主要针对相对平稳状态。

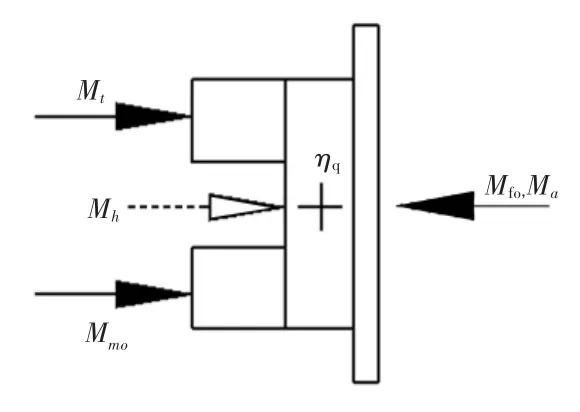
图4 动力合成与受力示意图

2.4 电动机相对助力比

助力车的主要特点就是具有电动机助力功能，恰当表征电动机助力程度具有重要意义。电动机助力矩与脚踏力矩应共同相对于中置链轮轴才具有比较意义，因此如下定义“电动机相对助力比”：电动机转换力矩与脚踏等效力矩之比，记为ξ。定义式为

显然，对于一定的相对助力比ξ，当处于相对平稳骑行状态时，平均脚踏力矩Mtp相对恒定，则电动机转换力矩Mmo也是相对恒定的。

2.5 助力状态下的动力波动性质

1）合成力矩的波动表达式和相对波动系数。在式（3）中，以脚踏瞬时力矩值Mt取代其平均力矩值Mtp，结合式（5），得助力状态下作用于中置链轮的瞬时合成力矩为

式中，Mh为瞬时合成力矩。结合式（1）得合成力矩波动表达式为

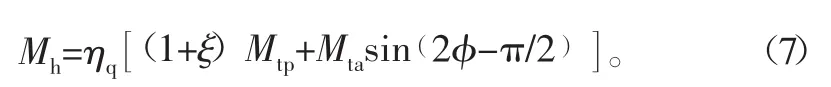
根据相对波动系数定义和式（7），得

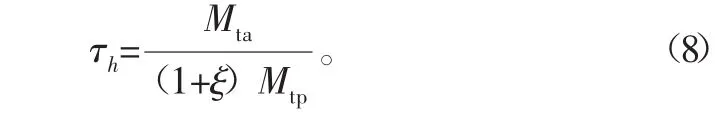
式中，τh为按平均脚踏力矩作对比跟踪助力的合成力矩相对波动系数。

2）合成力矩的波动性及其比较。以往的电动机助力形式为对瞬时脚踏力矩作实时比值跟踪，即式（5）中的Mtp代之为Mt，从而得到相应的瞬时合成力矩、相对助力比和相对波动系数表达式为:

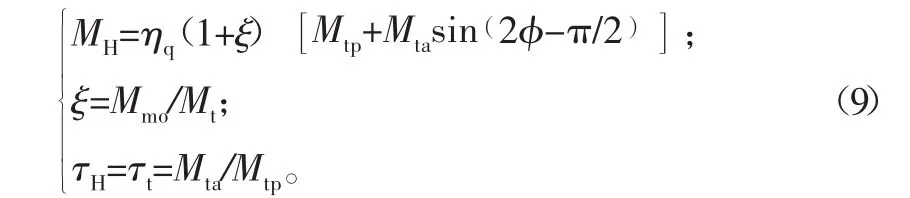
式中，MH、τH分别为按瞬时脚踏力矩作比值跟踪助力的合成力矩、相对波动系数。可以看出，这种场合下，对于一定的相对助力比ξ，由于瞬时脚踏力矩Mt是波动变化的，因此电动机转换力矩Mmo也是波动变化的。同时，对于τh和τH的比较

因此，与脚踏力矩的相对波动性比较，按瞬时脚踏力矩作实时比值跟踪助力的合成力矩相对波动性不变，但按平均脚踏力矩作比值跟踪助力的相对波动性减小，减小程度与助力比ξ成递增关系。图5为式（7）和式（9）的对比波动图线，从图5也可看出Mh比MH的波动性要小。

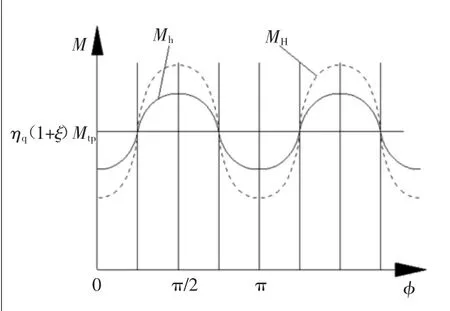
图5 合成力矩波动性对比示意图

3 新助力模式下的力学与运行特性分析

3.1 动力合成与力学特性

按照新助力模式特点，设脚踏力矩上设定值为Mt1，则当Mtp≥Mt1时，电动机启动助力。电动机启动前为纯脚踏驱动的非合成状态，在式（3）中，令Mmo=0，Ma=0，并根据式（4），得电动机启动助力条件为

两种动力混合作用后，经过加速阶段，达到相对稳定状态，则根据式（3）、式（5），得持续助力过程的动力合成与力学关系式：

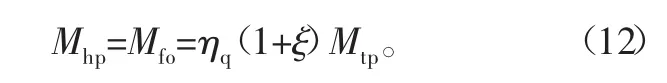
结合式（4），得

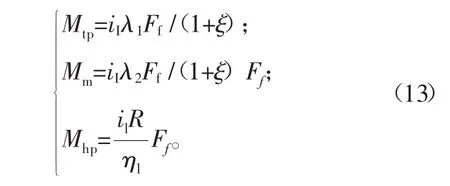
式中，λl、λ为体现助力车结构和效率的两个特征系数

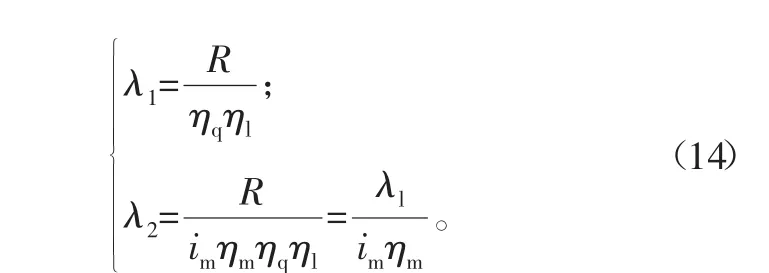
根据式（13），在行驶阻力Ff一定的情况下，Mtp与ξ成递减关系，Mm与ξ成递增关系。

3.2 持续助力条件

进入助力状态后，要实现持续助力行驶，且相对助力比ξ不小于一个最小期望值ξmin，即要满足：Mtp＞Mt2，ξ≥ξmin，则根据式（13），电动机相对助力比ξ应满足

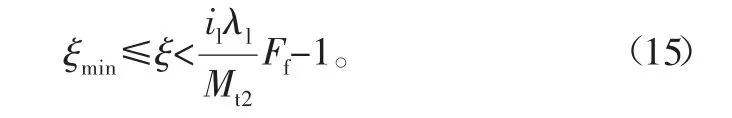
式中，Mt2为脚踏力矩下设定值。根据式（11）～式（15），得到下述结论：

1）当骑行者体力不支而需要较大助力时，可增大相对助力比ξ；也可减小il值，但会导致行驶速度减小；反之，当骑行者体力充沛，可选择较小相对助力比ξ，节约电能。

2）根据式（15），如需要持续助力，则对于每一种状态，都对应适当的ξ范围，满足式（15）的条件：如ξ过大，则Mtp下降，出现Mtp≤Mt2，继而出现电动机停止助力，从而Mtp又增大，当达到Mtp≥Mt1，再次启动电动机助力，如此循环，形成断续助力现象；如ξ过小，则不满足ξ≥ξmin。因此，为满足各种不同的要求，应设置适当多的助力比ξ选择挡位，最理想方式为无级挡位调整。

3）如果式（15）的右边不等式不能满足，但要求恢复持续助力状态，则调整方法：减小ξ挡位，或加大il，或联合上述调整。如按上述调整都不能实现，说明ξ挡位设置没有达到足够小的程度，或者行驶阻力已变得较小，没有满足式（11）要求的再次启动电动机助力的基本条件。

3.3 助力比、电动机功率和行驶阻力的关系

将式（4）的第3、4式带入式（13）的第2式，并注意ωmo=ωt，得

式（16）就是助力比、电动机功率和脚踏速度、行驶阻力的综合关系式。从式（16）又得

可以看出，电动机输出功率与行驶阻力Ff、脚踏速度ωt、助力比ξ均呈递增关系。从式（16）还可推出：

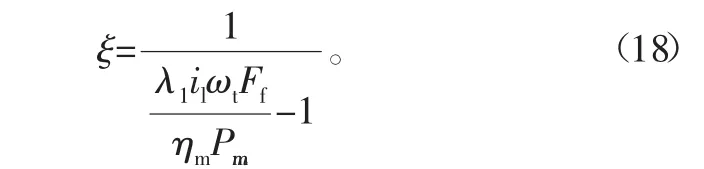
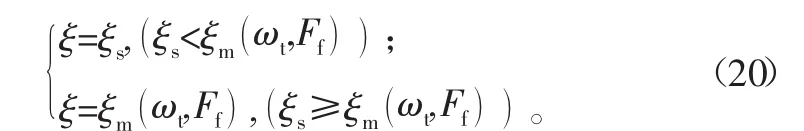
式中，ξs为选择的助力比值。此时的ξ为电动机实际执行的助力比。显然，如果需要持续助力，还需满足式（15）。一些国家规定，当行驶速度达到一定值后，限制助力比，使之按一定方式逐步下降，随着行驶速度达到最大限值而助力比为0[7,11]。如要执行这一要求，则可将之作为附加条件进行控制。

4 试验验证

试验方法主要采用对样车实际骑行和测定的方式，验证合成力矩的波动性及其比较、各参量的调整效果和持续助力条件及助力状态变化特点。方法要点：1）根据实际样车结构确定相关结构参数、传动比和传动效率。2）骑行阻力变化的实现方法。a.在平整场地上试验，适当调整负重，实现较小阻力的调整，Ff=f1W，其中f1为路面摩擦因数，W为车与负重总重。b.采用骑行试验板，通过调整试验板的斜度和负重，实现较大阻力的调整，其中f2为试验板面摩擦因数，θ为斜度。3）脚踏力矩和脚踏速度通过减速机的传感装置检测，电动机输出力矩、功率通过监测控制器而得到。4）相应多次改变阻力Ff、脚踏速度ωt，调整助力比ξ值、变速比il，记录脚踏力矩Mtp、电动机力矩Mm、功率Pm和转速ωm；同时辅以骑行者的感觉对比。

在考虑误差因素影响的情况下，试验结果与本文分析得出的力学关系特性是符合的，各参量调整结果符合分析结论，如出现断续助力现象、恢复持续助力状态、无法进入助力状态等；并从骑行的波动性和舒适感觉上印证了合成力矩相对波动性的变化和对比特点。

5 结语

1）脚踏力矩变化近似呈正弦波形式，采用相对波动系数可有效描述脚踏力矩、合成力矩的波动性。脚踏等效力矩为脚踏旋转一周力矩变化的平均值，将其作为跟踪助力对比值和用于分析计算是合理的，并且可减小合成力矩的相对波动性。

2）采用设定助力启动阈值、可调助力比的新助力模式，可避免阻力较小时仍然持续助力而浪费电能的现象，以及在行驶过程具有更多的适应实际状况的选择调整方式。

3）新助力模式下，对于每一种状态，都对应适当的助力比ξ的选择范围，ξ值要适当，如ξ过大，可能会出现断续助力现象；如ξ过小，则达不到助力要求。因此，应设置适当多的助力比ξ选择挡位，理想方式为无级挡位调整。