利用FastICA和三阶相关函数的多天线辅助NPLC-DS-CDMA扩频码盲估计

尹 辉 赵知劲

(杭州电子科技大学通信工程学院，浙江杭州 310018)

1 引言

长码直扩CDMA(long-code direct sequence code division multiple access，LC-DS-CDMA)信号在一个扩频周期内有多个信息符号，具有很强的保密性，因此在军事和民用通信系统广泛运用[1-3]。由于长码周期过长，通常在接收端很难截获包含一个完整扩频码周期的信号，因此扩频码盲估计更加困难。

针对周期LC-DS-CDMA扩频码盲估计，文献[4]将LC-DS-CDMA信号等效为含有缺失数据的短码直扩信号，再利用嵌套迭代最小二乘投影算法估计扩频序列；文献[5]利用m序列的三阶相关函数(triple correlation function，TCF)峰值点不同的特点构造TCF的特征信息矩阵，然后将LC-DS-CDMA信号TCF值与特征信息矩阵匹配，估计各用户扩频码；文献[6]和文献[7]对LC-DS-CDMA信号分段，再利用FastICA算法估计扩频码片段，将扩频码片段拼接得到扩频码。上述LC-DS-CDMA信号的扩频码盲估计方法都只针对周期信号，截获的接收信号需要包含完整的扩频码周期。针对非周期(non-periodic，NP)扩频码盲估计，文献[8]利用不同周期m序列三阶相关函数存在共同峰的特点，计算NPLC-DS-DSSS信号TCF值，筛选共同峰得到扩频码本原多项式；文献[9]在此基础上采用拟合优度检验对共同峰进行筛选，提高了估计正确率。文献[8]和文献[9]针对的是单用户长码直扩信号。对于非周期LC-DS-CDMA信号，由于信号结构更加复杂，且接收信号没有包含一个完整周期扩频码，所以扩频码的盲估计难度很大，关于此类信号的研究成果还未见公开报道。

本文针对多天线NPLC-DS-CDMA信号，将接收信号矩阵进行奇异值分解，对左奇异向量张成的信号子空间利用FastICA算法进行盲源分离[10]，得到各个用户的扩频信号；对扩频信号利用延迟相乘法消除信息码影响，然后计算三阶相关函数[11]，通过比较TCF估计值与理论值的距离筛选估计的TCF峰值点，最后利用矩阵斜消法得到扩频码本原多项式。

2 信号模型

第k个天线的接收信号基带模型可表示为

l=1,2,…,L

(1)

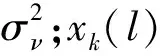
式(1)可表示为矩阵形式

yk=Sak+vk

(2)

其中，ak为第k个天线的接收增益，ak=[ak1ak2…akr]T，S为扩频信号矩阵，S=[s1s2…sR]，S是一个L×R的矩阵。则K个天线接收信号矩阵为

Y=SA+V

(3)

式中，Y为接收信号矩阵；A为接收增益矩阵。

3 算法

3.1 基于FastICA算法的扩频信号盲估计

对式(3)中接收信号Y进行奇异值分解得到最大的R个奇异值对应的左奇异特征向量U，特征向量U的列向量张成的子空间与扩频信号矩阵S的列向量张成的子空间属于同一个子空间，假设它们之间存在的线性变换为T，则：

U=TS

(4)

式(4)是一个典型的盲源分离模型，估计扩频信号矩阵S就相当于从特征向量U中分离源信号，利用FastICA算法可以完成扩频信号矩阵的估计。

首先对U进行白化预处理，从而简化独立分量提取过程，提高算法收敛性。如式(5)所示，白化矩阵为B0，白化后得到白化向量为Z。

Z=B0U

(5)

利用主分量分析，得到白化矩阵为

(6)

其中Λ和Us分别代表信号U的协方差矩阵的特征值矩阵和特征向量矩阵。得到白化向量Z后，估计分离矩阵W的FastICA算法的迭代如下：

wt=wt/‖wt‖

(7)

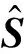
(8)

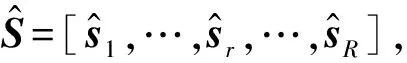
3.2 扩频码TCF估计值

理论上，m序列cr(l)的TCF为：

Cr(p,q)=E{cr(l)cr(l+p)cr(l+p)}

(9)

完整周期的cr(l)的TCF值为：

(10)

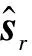
(11)

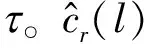
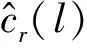
(12)

3.3 扩频码TCF峰值点检测

根据式(12)可以得到扩频码cr(l)的TCF值。TCF值表示成矩阵形式如下：

理论上，m序列的TCF峰值点和非峰值点可以清楚区分，但是由于噪声干扰、接收长度受限和延迟相乘带来的误差，估计得到的TCF与理论值存在较大偏差，如果仅通过设置门限值提取峰值点，容易产生漏检和错检，而且计算量较大，因此本文根据m序列性质，对TCF峰值点进行筛选，以获得更准确的峰值点。

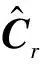
(13)

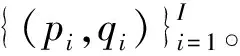
通过粗筛选得到I个坐标点后，需要对这些坐标点进行更精确的筛选。由m序列的性质[13]可知，若m序列在(p,q)处存在峰值点，则(2ipmodNr,2iqmodNr),i=0,1,2,3,…处也存在峰值点。

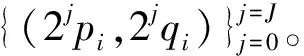
(14)

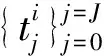
根据m序列的三阶相关性质可知，不同m序列具有不同分布的TCF峰值点，利用矩阵斜消法从两个TCF峰值点多项式得到m序列的本原多项式[14]，即为扩频码本原多项式。

综上所述，本文提出的多天线辅助NPLC-DS-CDMA信号的扩频码本原多项式盲估计算法主要步骤如下：

(1)将多天线NPLC-DS-CDMA信号按式(2)和式(3)构建成矩阵信号Y；

(2)对Y进行奇异值分解，得到左奇异特征向量U;

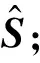
(4)根据式(13)和式(14)对三阶相关值进行筛选求出峰值点，利用矩阵斜消法估计扩频码本原多项式。

4 算法仿真与性能分析

①算法性能与天线个数的关系。用户个数R=3，3个用户依次使用表1中11阶m序列作为扩频码，接收信号长度为L=1000，天线个数分别为K=10、K=15和K=20时，本文算法的正确率曲线如图1所示。

从图1可知，天线个数越多，扩频码本原多项式估计正确率越高，算法性能越好。由于每个天线接收的信号承载着相同的扩频码信息，天线个数越多，获得的扩频码信息越多，FastICA方法从中分离出的扩频信号误差减少，因此扩频码本原多项式估计正确率提高。

②算法性能与信号长度的关系。天线个数K=10，用户个数R=3，3个用户依次使用表1中11阶m序列作为扩频码，接收信号长度分别为L=500、L=1000和L=1500时，本文算法的正确率曲线如图2所示。

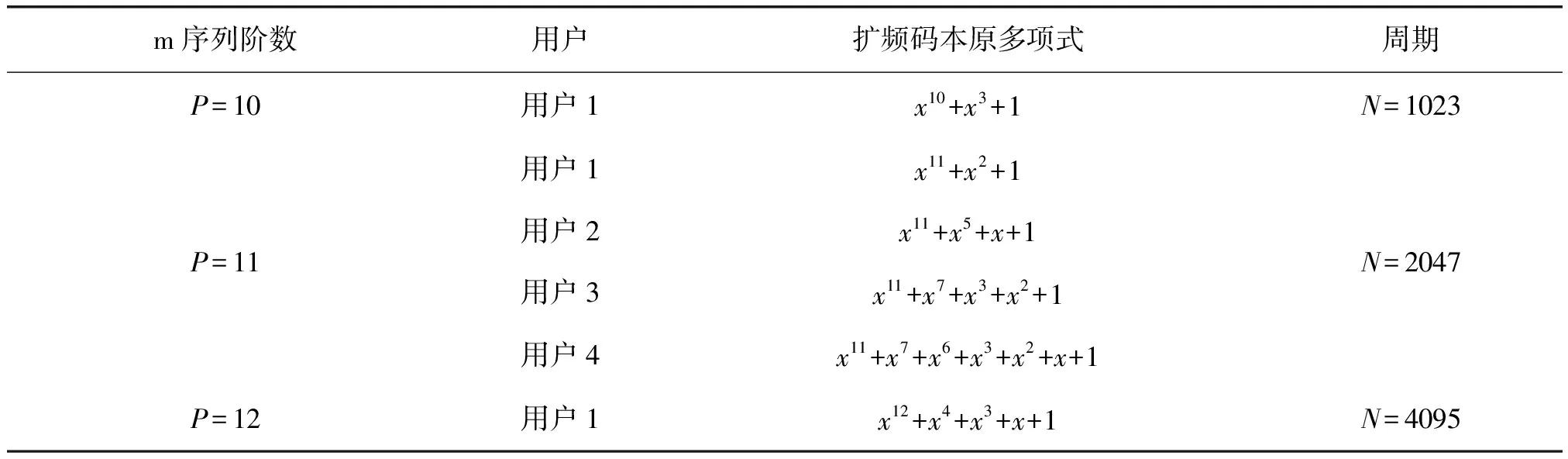
表1 不同用户使用的扩频码

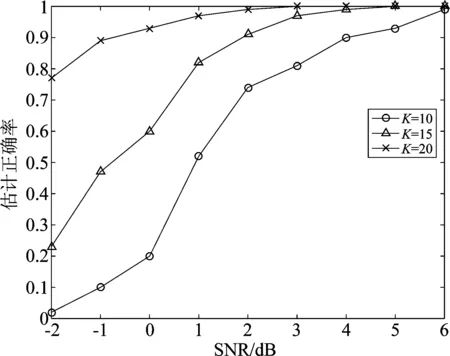
图1 算法性能与天线个数的关系

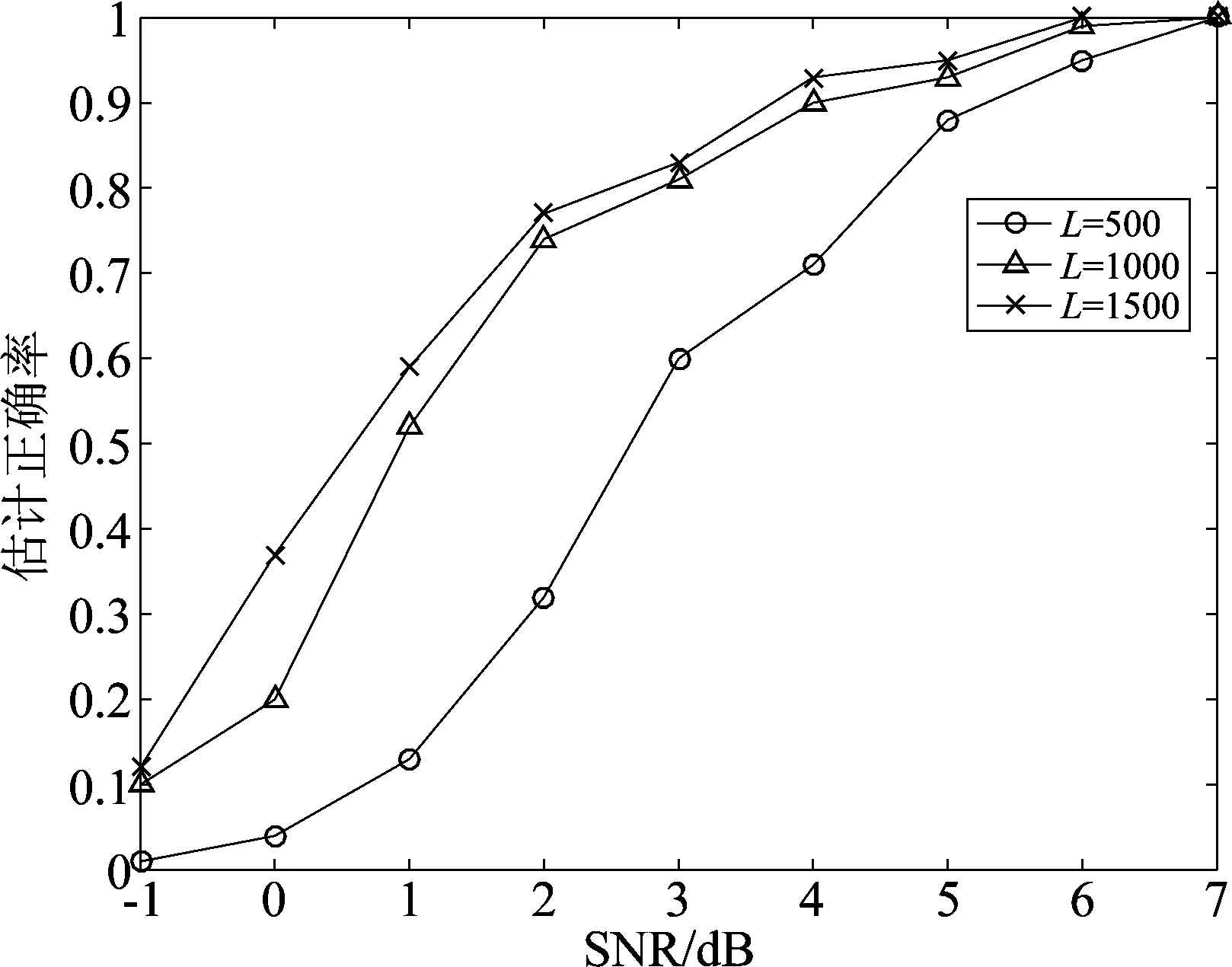
图2 算法性能与信号长度的关系

从图2可知，接收信号越长，扩频码本原多项式估计正确率越高。因为接收信号越长，估计得到的延迟后扩频码片段越长，计算的TCF值越接近于完整周期扩频码的TCF值，更容易筛选得到正确的TCF峰值点，因此扩频码本原多项式估计正确率更高。

③算法性能与用户个数的关系。天线个数K=10，接收信号长度为L=1000，依次使用表1中11阶m序列作为扩频码，用户个数为R=2、R=3和R=4时，本文算法的正确率曲线如图3所示。

由图3可知，用户个数增多，本文算法估计性能下降。因为用户个数增多，用户之间的干扰增大， FastICA算法分离的扩频码误差增加，从而使本文算法的估计正确率下降。

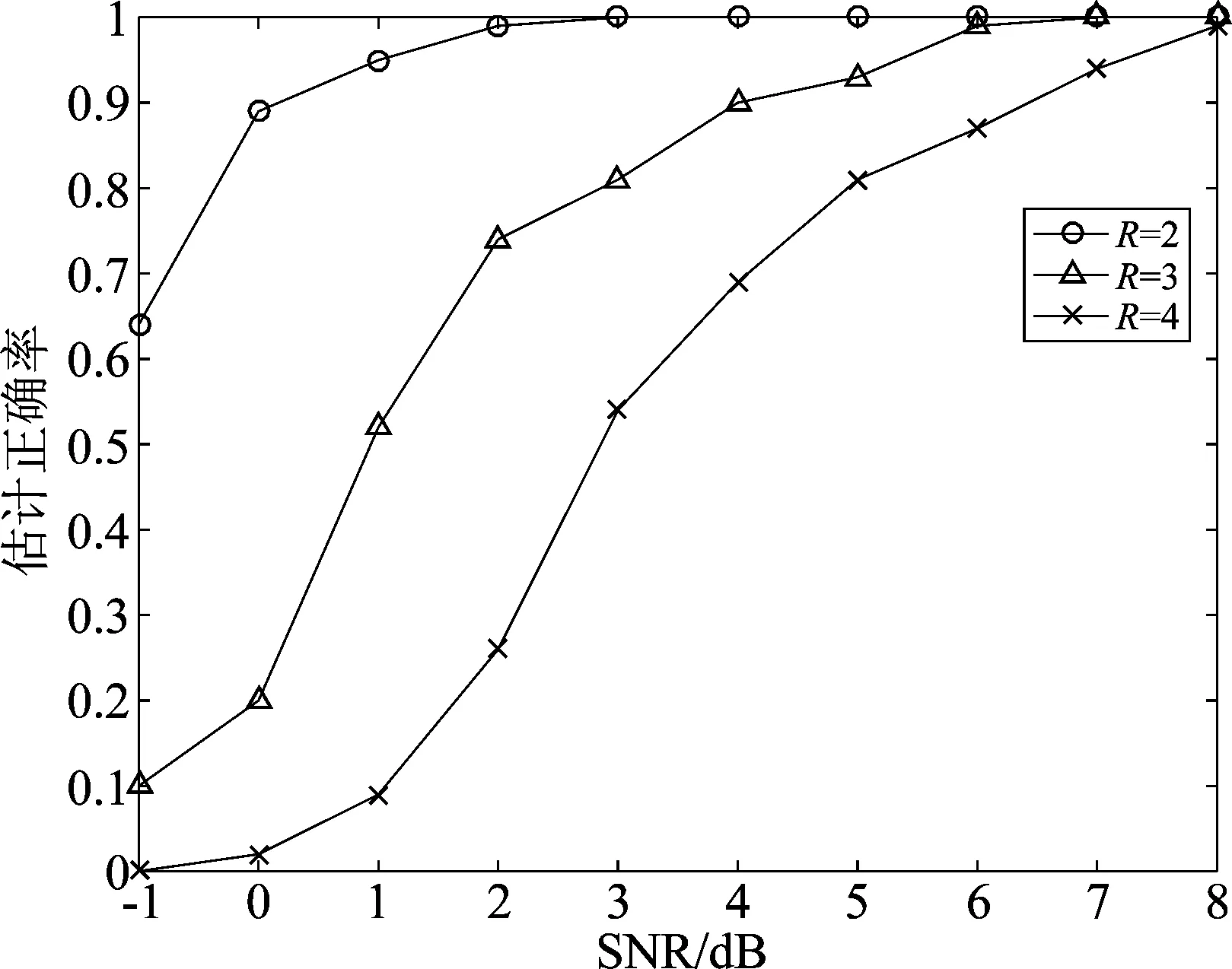
图3 算法性能与用户个数的关系

④算法性能与扩频码周期长度的关系。天线个数K=10，接收信号长度为L=1000，用户个数R=3，信号1的3个用户分别使用表1 中10阶、11阶和12阶m序列的用户1的本原多项式产生周期为N1=1023、N2=2047和N3=4095的扩频码，信号2中3个用户依次使用表1中11阶m序列作为扩频码即N1=N2=N3=2047。信号1和信号2的R个用户扩频码本原多项式估计正确率如图4(a)所示；信号1中每个用户扩频码本原多项式估计正确率如图4(b)所示。

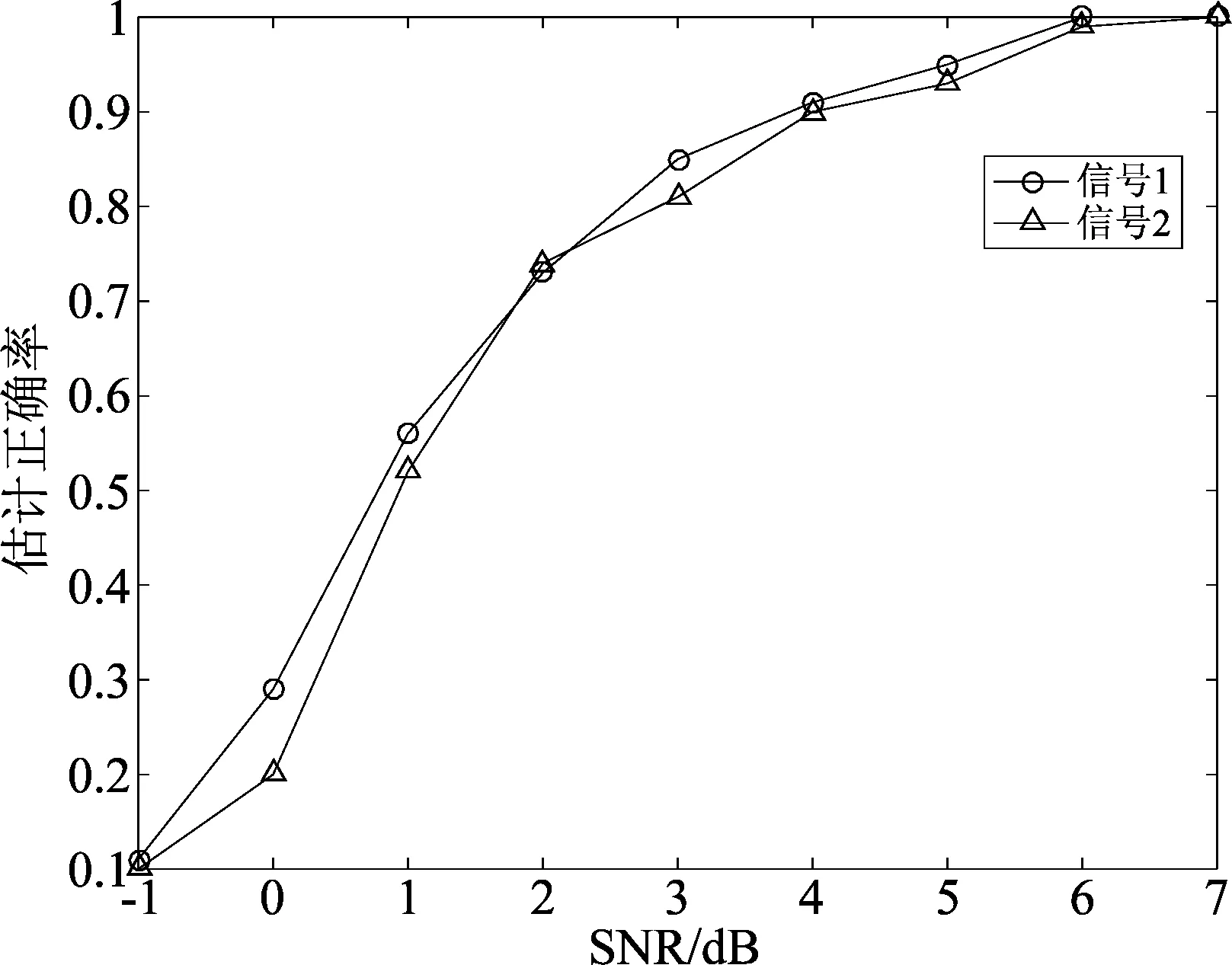
图4(a) 算法性能与扩频码长度的关系

图4(b) 信号1各个用户扩频码估计性能

由图4可知，本文算法适用于各个用户扩频码周期长度不同的情况；当接收信号长度一定时，扩频码周期越小，本原多项式估计正确率越高。因为扩频码周期越小，接收信号中包含的该扩频码的信息越完整，TCF峰值点估计越准确，扩频码本原多项式估计正确率越高。

⑤与文献[5]和文献[9]算法对比。目前无公开报道关于NPLC-DS-CDMA信号扩频码盲估计算法，文献[5]针对周期LC-DS-CDMA信号，文献[9]针对单用户NPLSC-DSSS信号，同样适用于单用户NPLC-DSSS信号，为了更好地验证本文算法性能，比较本文算法与文献[5]、文献[9]算法对NPLC-DS-CDMA信号扩频码估计性能。用户个数R=3，3个用户依次使用表1中11阶m序列扩频码即N1=N2=N3=N=2047，接收信号长度分别为L=N/2，天线个数K=10，对每个天线接收到的信号应用文献[5]以及文献[9]算法估计扩频码本原多项式，统计从所有天线接收信号中估计得到的扩频码本原多项式，选取出现次数最多的R个本原多项式作为文献[5]及文献[9]算法估计所得的扩频码本原多项式。本文算法和文献[5]、文献[9]算法的R个用户扩频码估计正确率如图5所示。

由图5可知，对于NPLC-DS-CDMA信号扩频码盲估计，本文算法性能优于文献[5]和文献[9]算法。文献[5]算法适用于周期CDMA信号，文献[9]算法适用于单用户非周期直扩信号，二者对NPLC-DS-CDMA信号估计性能严重恶化，本文算法能够实现NPLC-DS-CDMA信号的扩频码盲估计，且随着信噪比增加，估计正确率增大。

图5 算法性能对比

5 结论

本文针对NPLC-DS-CDMA信号的扩频码盲估计，利用多天线辅助、奇异值分解和FastICA算法从接收信号矩阵中估计得到扩频信号，利用延迟相乘法去除扩频信号中的未知信息码，再估计三阶相关函数的峰值点，最后利用峰值点估计得到扩频码本原多项式。

[1] Mirbagheri A, Yoon Y C. A blind adaptive receiver for interference suppression and multipath reception in long-code DS-CDMA[C]∥IEEE International Conference on Communications. IEEE, 2015:242-246.

[2] 熊刚, 彭勃. 一种改进的周期长码扩频序列盲估计方法研究[J]. 通信技术, 2015, 48(3):272-277.

Xiong Gang, Peng Bo. A Modified Blind Estimation in PLC DSSS Communications[J]. Communications Technology, 2015,48(3):272-277.(in Chinese)

[3] Xia W, Zhou Y, Meng Q. Run-length method for determining the segmentation length based on the segmentation long-code blind estimation[J]. Iet Signal Processing, 2016, 10(7):732-736.

[4] 张天骐, 强幸子, 马宝泽,等. 基于最小二乘的同步多用户非周期长码直扩信号扩频序列估计[J]. 电波科学学报, 2016, 31(6):1113-1122.

Zhang Tianqi，Qiang Xingzi, Ma Baoze，et al. Estimation of the spread spectrum sequence for synchronous multi-user a periodic long-code DSSS signals based on least squares[J]. Chinese Journal of Radio Science,2016, 31(6):1113-1122. (in Chinese)

[5] 赵知劲, 强芳芳, 顾骁炜,等. 利用三阶相关特征信息的周期长码扩频信号伪码盲估计[J]. 信号处理, 2016, 32(6):739-745.

Zhao Zhijin, Qiang Fangfang, Gu Xiaowei,et al. Blind Estimation of Pseudo-Random Codes in Period Long Code Spread Spectrum Signals by Using Triple Correlation Feature Information[J]. Journal of Signal Processing,2016, 32(6):739-745. (in Chinese)

[6] 陆凤波, 黄知涛, 姜文利. 基于FastICA的CDMA信号扩频码盲估计及性能分析[J]. 通信学报, 2011, 32(8):136-142.

Lu Fengbo, Huang Zhitao, Jiang Wenli. Blind estimation of spreading sequence of CDMA signals based on Fast-ICA and performance analysis[J]. Journal on Communications, 2011, 32(8):136-142. (in Chinese)

[7] 任啸天, 徐晖, 黄知涛,等. 基于FastICA的CDMA信号扩频码优化盲估计[J]. 电子学报, 2012, 40(8):1532-1538.

Ren Xiaotian, Xu Hui, Huang Zhitao, et al. Fast-ICA Based Optimize Blind Estimation of Spreading Sequence of CDMA Signals[J]. Acta Electronica Sinica, 2012, 40(8):1532-1538. (in Chinese)

[8] 赵知劲, 顾骁炜, 沈雷,等. 非周期长码直扩信号的伪随机码盲估计[J]. 通信学报, 2015, 36(5):23-30.

Zhao Zhijin, Gu Xiaowei,Shen Lei, et al. Blind estimation of pseudo-random codes in non-periodic long code direct-sequence spread-spectrum signals[J]. Journal on Communications, 2015, 36(5):23-30. (in Chinese)

[9] 赵知劲, 强芳芳, 李淼,等. 利用拟合优度检验的NPLSC-DSSS信号伪码盲估计[J]. 电子与信息学报, 2017, 39(3):749-753.

Zhao Zhijin, Qiang Fangfang, Li Miao, et al. Blind Estimation of Pseudo-random Noise Codes in NPLSC-DSSS Signals Based on Goodness of Fit Test[J]. Journal of Electronics & Information Technology, 2017, 39(3):749-753. (in Chinese)

[10] Singh A, Anand R S. Overview of the performance of fast ICA and DUET for blind source separation of multiple speakers[C]∥Recent Advances in Electronics & Computer Engineering. IEEE, 2016:296-300.

[11] 俎云霄, 汪芙平, 王赞基. m-序列的三阶相关函数及其峰值特性[J]. 天津大学学报, 2004, 37(9):836- 841.

Zu Yunxiao, Wang Fuping, Wang Zanji. Triple Correlation Function of m-Sequence and Its Peak Feature[J]. Journal of Tianjin University, 2004, 37(9):836- 841. (in Chinese)

[12] 张天骐, 易琛, 张刚,等. 基于高斯列消元法的线性分组码参数盲识别[J]. 系统工程与电子技术, 2013, 35(7):1514-1519.

Zhang Tianqi, Yi Chen, Zhang Gang, et al. Blind identification of parameters of linear block codes based on columns Gaussian elimination[J]. Systems Engineering & Electronics, 2013, 35(7):1514-1519. (in Chinese)

[13] 邱秩修. 长码直扩信号中的扩频序列估计[D].成都：电子科技大学, 2012.

Qiu Zhixiu. Estimation of the Spreading Codes of the Long-Code Direct Sequence Spread Spectrum[D]. Chengdu: University of Electronic Science and Technology of China,2012. (in Chinese)

[14] 张晓林, 佟婧, 李佑虎. 高阶统计分析的m序列检测新方法[J]. 哈尔滨工程大学学报, 2010, 31(3):386-390.

Zhang Xiaolin, Tong Jing, Li Youhu. A New Method for m-sequence Detection using Higher-order Statistics[J]. Journal of Harbin Engineering University, 2010, 31(3):386-390. (in Chinese)