DELTA并联机器人路径规划设计

陈红亮，孔宇超

(浙江水利水电与汽车工程学院 机械学院，浙江 杭州 310018)

在机器人技术的应用与研究中，路径规划问题是一个重要研究内容之一.[1-2]机器人在执行实际工作过程中，其运动起点和运动终点之间不可避免地需要绕开或避免干涉位置、障碍物和奇异位置点等区域，所以机器人路径规划问题也相对比较复杂[3-6].国内外许多学者对最优时间轨迹规划进行了深入研究，大多采用三次多项式、高阶多项式及B样条曲线等方法在操作空间或关节空间对机器人进行轨迹规划，得到了速度、加速度及转矩连续的运行曲线，保证了机器人运行的稳定性，减少了对机械的刚性冲击[3-6].不过这些方法需要大量的计算和计算机编程.本文借助ADAMS软件，以最为成功应用于工业领域的并联机构之一DELTA并联机器人为例，对其进行运动学的正解和逆解求解，并规划其工作路径.

1 DELTA并联机器人结构

并联机器人由动平台和定平台通过至少两个独立的运动链相连接，机构具有两个或两个以上自由度，且以并联方式驱动的一种闭环机构.其特点为无累积误差，精度较高；驱动装置可置于定平台上或接近定平台的位置，这样运动部分重量轻，速度高，动态响应好[3-4].

本文研究的DELTA并联机器人结构示意图(见图1)，其组成为动平台A，三组上连杆AiBi，三组下连杆BiCi(i=1～3)和定平台C组成，其自由度为3.其三维示意图(见图2).

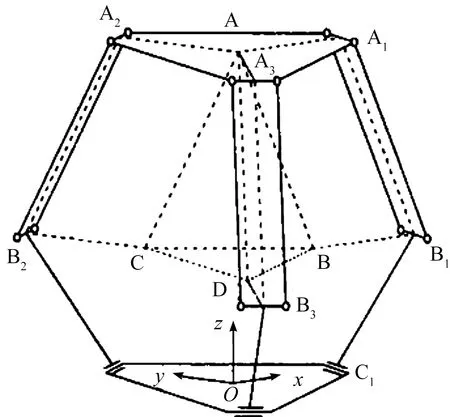
图1 DELTA并联机器人示意图

图2 DELTA并联机器人三维模型图

那么连杆A1B1、A2B2、A3B3分别沿A1A,A2A,A3A平移,并交于运动平台中心A.当3个输入杆输入角度给定,动平台的位置可以由式(1)求得[7].

i=1,2,3

(1)

式中:r1—运动平台铰链点所在圆半径；

φ—运动平台铰链点分布角.

用这种方法求解需要大量编程和复杂数值计算，本文采用ADAMS软件求解.

2 基于ADAMS软件DELTA并联机器人正解

所谓机器人的正解，是给定机器人各关节的角度、位移等，计算出机器人末端的空间位置和姿态.对于并联机器人而言，其位置正解计算过程中需要求解多元高度耦合的非线性方程，因此相对比较困难.

ADAMS是虚拟样机分析的应用软件，用户可以运用该软件非常方便地对虚拟机械系统进行静力学、运动学和动力学分析[8-11].

作者采用ADAMS软件分析DELTA并联机器人的末端位置.将DELTA并联机器人导入ADAMS软件，添加约束和驱动，在定平台C处，三个主动副的驱动分别为30×sin(180×time)，30×sin(180×time-120)，30×sin(180×time+120)，驱动角度单位为度，在软件中仿真运行时间是2 s，测得动平台位移(见图3，图4).

图3 动平台X方向和Y方向的位移变化曲线

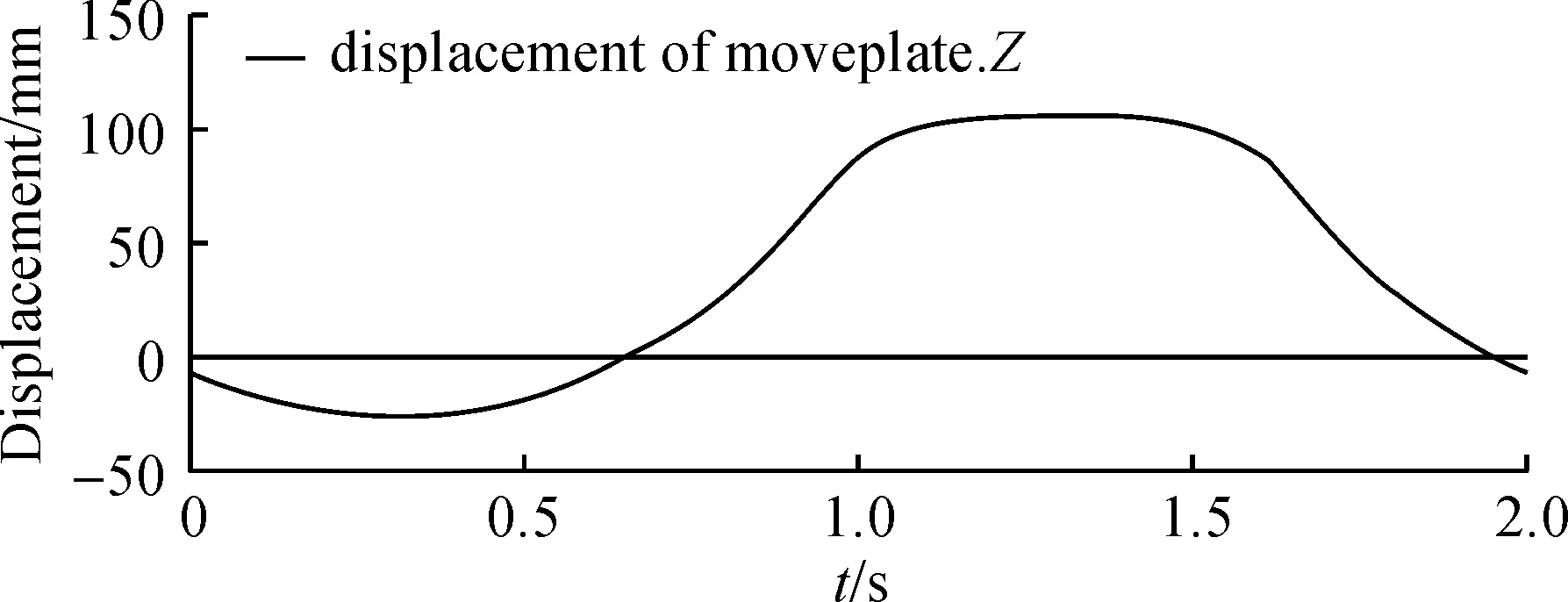
图4 动平台方向的位移变化曲线

3 基于ADAMS软件DELTA并联机器人运动轨迹规划

将机器人末端操作手避开障碍的各点连接起来，构成机器人末端操作手运动轨迹.已知机器人末端位置，求解机器人各关节角度和位移，称之为机器人逆解.运动轨迹规划也就是求解机器人位置逆解.

ADAMS软件的点驱动功能[7-8]，可以在机器人末端操作手实现6个自由度分别定义其运动轨迹，仿真时自动合成运动，此时在主动副上建立测试函数，仿真结束后，将测试函数转化为样条曲线导出；然后将样条曲线添加到主动副的驱动上，并取消点驱动功能，再进行仿真，可以复现点驱动机器人末端操作手运动轨迹，从而实现机器人轨迹规划.

不失一般性，本文设计了DELTA机器人末端操作手运动轨迹(见图5)，那么机器人末端操作手中坐标系中各个运动规划方向为：

图5 机器人末端操作手运动轨迹

X方向：40×cos(2×180d×time)

Y方向：40×sin(2×180d×time)

Z方向：-20×time

在DELTA机器人的主动副上添加测试函数，仿真运行机器人模型，可以求得其主动副的运动轨迹(见图6).将图6曲线上导出为表格形式，如何分别以样条曲线插值方式添加到主动副驱动上，并屏蔽末端操作手的点驱动，再仿真运行机器人，结果实现机器人轨迹规划.

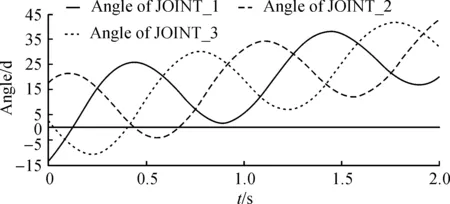
图6 主动副的运动轨迹

4 结 语

本文采用ADAMS软件仿真求解DELTA机器人的运动学正解和逆解，并将其逆解导出数值解，将数值解转化为样条曲线，并将该曲线添加到主动副的驱动上，可以实现机器人运动轨迹规划.该方法不需要大量编程就易于实现机器人的运动轨迹规划，从而可以加快机器人研发进度.