平底矩形断面渐扩散水跃跃后水深的计算
傅铭焕,惠祥明,吴留伟,田 甜,侯 毅,卢志男
(浙江省水利水电勘测设计院,浙江 杭州 310002)
在实际工程中,往往遇到溢洪道或泄洪洞的出口较窄而下游河床较宽的情况,此时常采用渐扩式消力池来平顺衔接上下游水流.发生于渐扩式消力池中的水跃称为渐扩散水跃.张志恒[1]试验研究了平底矩形断面渠道渐扩式消力池的水力特性,研究发现,在相同流量下渐扩式消力池跃后水深较一般矩形二元水跃小4%~14%.W. H. HAGER[2]的研究也表明,在相同来流情况下,渐扩式消力池衔接上游水流所需的下游尾水水深较一般矩形消力池小.陈椿庭等[3]的研究发现,当渐扩式水跃跃后断面宽度与跃前断面宽度比b2/b1=2时,所需的下游水深较一般矩形消力池可减小1/10.可见,渐扩式消力池的布置既是工程实际所需,同时渐扩式消力池又具有很好的经济效益.而渐扩散水跃跃后水深和水跃长度作为渐扩式消力池体形的重要设计参数,为广大学者所研究.学者们通过求解渐扩式消力池跃前和跃后断面动量方程的传统方法,研究渐扩式水跃共轭水深的变化规律[1-7].但各家学者出于对渐扩式消力池边墙反力认识的不同,在计算渐扩式水跃跃后水深时是否应该考虑边墙反力,以及对边墙反力的计算方法目前尚未统一.傅铭焕等[8]绕过消力池边墙作用力,通过分析渐扩式水跃局部阻力系数随一般二元水跃局部阻力系数的变化规律,同时利用能量方程推导了渐扩式水跃跃后水深新的计算方法,并在边墙扩散角θ<9°时获得较好的计算效果,为渐扩散水跃跃后水深的研究提供新的思路.文献[9]分析了现阶段渐扩散水跃水跃长度的计算公式,发现各学者提出的水跃长度计算值偏离较大.
平底矩形断面渠道渐扩散消力池水跃跃后水深的研究远没有一般矩形消力池研究的深入和透彻,笔者尝试通过新的途径,避开边墙反力这一问题焦点,寻找新的方法研究渐扩散水跃跃后水深,为平底矩形断面渠道渐扩式消力池体形设计提供新的参考.
1 渐扩式消力池绕流阻力系数
实际液体沿固壁曲面流动时,若液体压力梯度沿程逐渐增大,主流会从某个位置开始脱离壁面以减少水流扩散,此时下游壁面附近出现回流现象,这种现象称为边界层流动的分离,又称为边界层脱体现象[10].闸下水流由较窄渠道突然扩散到较宽渠道时,边壁水流与壁面发生脱离,主流沿其流动的垂直方向发生扩散,并在扩散区形成回流,此时回流区与其相邻的主流存在压差.傅铭焕等[11]假定此压差作用力是由于渠道宽度突然扩散而对主流形成的绕流阻力(其作用方向与主流一致),并提出了突扩式消力池的新的水跃动量方程并获得了很好的计算效果.
矩形扩散水跃水力计算新公式[5]的试验表明:渐扩散消力池边墙压力并非静压分布,并且小于静压;当边墙扩散角θ>9°时,下泄水流会出现脱离壁面现象,在边墙内壁处有明显的回流产生.毛昶熙[12]的试验亦表明,当渐扩散消力池下游不设辅助消能工,边墙内壁出现明显回流时的边墙扩散角约为θ=7°.可见,下泄水流流经渐扩散消力池时会在边墙某处发生脱离,但对扩散角为多大,消力池边墙才会产生明显的回流,尚需进一步研究.作者尝试将文献[13]提出的突扩消力池绕流阻力公式应用到渐扩式消力池,来研究其水跃跃后水深计算的可行性.
平底矩形断面渠道渐扩散消力池中由于扩散而形成的回流徘徊于边壁附近,并排挤外流,此时回流区与其相邻的主流存在压差.假定由此产生的压差作用力是由于渠道宽度逐渐扩散而对主流形成的绕流阻力,其作用方向与主流一致,如图1所示,图1为一渐扩式消力池示意图.图中F绕即为因边墙扩散而形成的绕流阻力;P1和P2分别为跃前断面和跃后断面的动水压力;v1和v2分别为跃前断面和跃后断面的平均流速;b1和b2分别为跃前和跃后断面的消力池宽度;h1和h2分别为跃前和跃后断面水深;Ff为水跃段消力池底板对水流产生的壁面阻力;Lr为水跃旋滚长度;θ为消力池边墙扩散角.
对图1中跃前断面和旋滚末端断面列动量方程,设动量修正系数β1=β2=β修,可得:
β修γQ(v2-v1)/g=P1-P2+F绕-Ff
(1)
式中:γ—水流的重度,γ=ρg,ρ—水流密度,
g—水流重力加速度;Q—下泄水流流量.
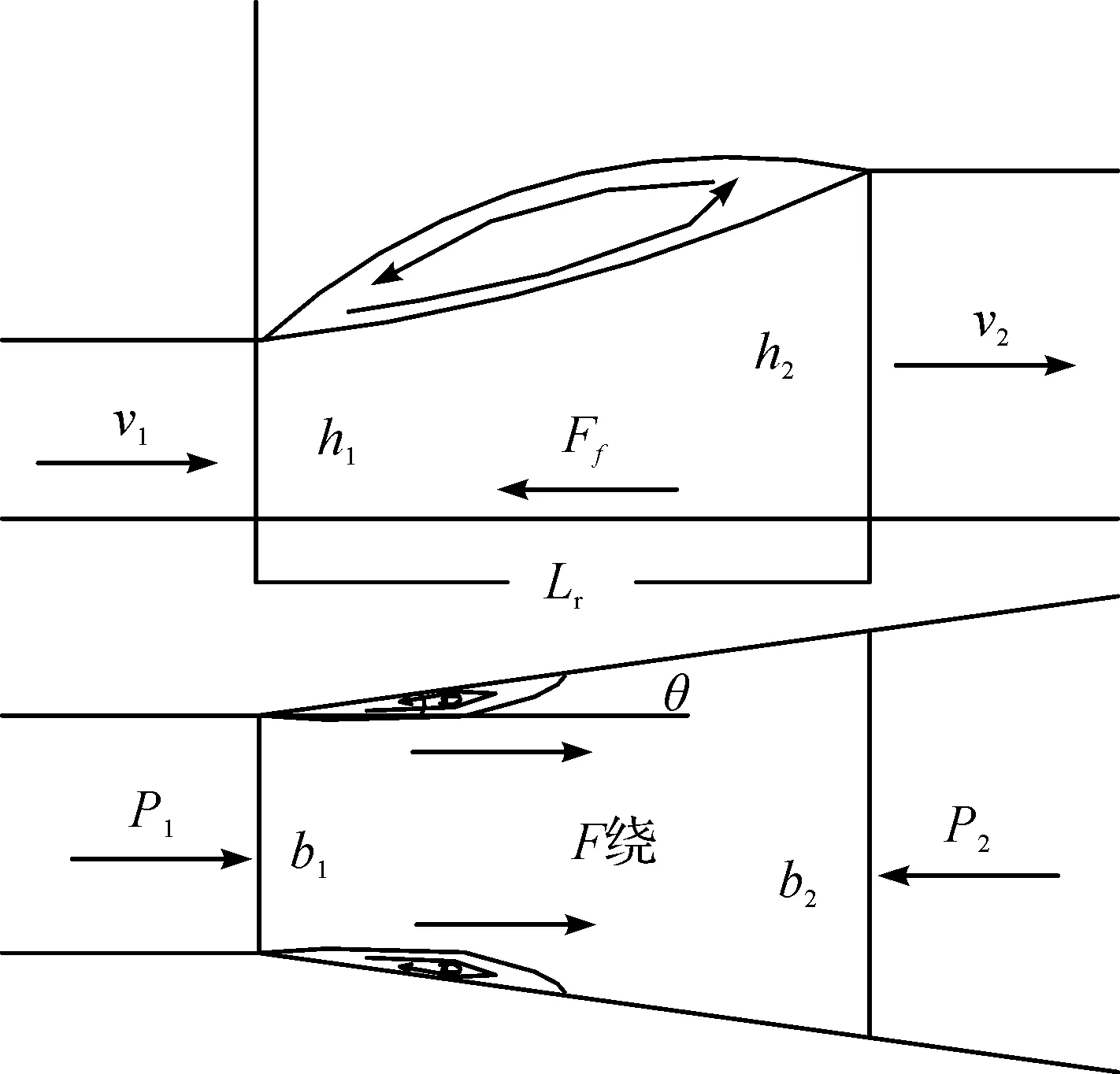
图1 平底矩形断面渠道渐扩式水跃示意图
文献[13]和文献[14]的研究表明,对于一般混凝土壁面,不计壁面阻力,对共轭水深比和相对能量损失影响很小.因此,本文忽略壁面阻力Ff的影响,同时出于简便考虑,假定动量修正系数β修=1,则公式(1)变为:
γQ(v2-v1)/g=P1-P2+F绕
(2)
绕流阻力F绕可表示为[11]:
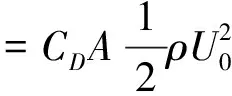
(3)
式中:CD—绕流阻力系数;A—阻水面积;
U0—绕流前水流平均流速.
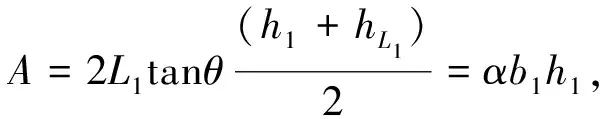

(4)
式中:CL—绕流阻力的综合阻力系数.
由公式(4)可知,要求得绕流阻力,需先确定综合绕流阻力系数,将公式(4)进行变形,可得综合绕流阻力系数CL的表达式,即:
(5)
对于综合绕流阻力系数,目前尚无成熟的理论计算方法,多通过试验确定.
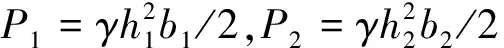
(6)

矩形扩散水跃的水力计算[1]实测的渐扩散消力池水工模型试验值(见表1),在此计算过种中并未给出水跃区水跃旋滚长度的试验值,但其给出了水跃旋滚长度实测值的拟合公式,即:
Lr=0.077h1(mFr1)1.5
(7)
式中:m=1/tanθ.
本文用公式(7)计算的水跃旋滚长度代替试验实测的水跃旋滚长度值.
由图1可知,水跃旋滚末端的消力池宽度b2可用下式计算,即
b2=2Lrtanθ+b1
(8)
根据矩形扩散水跃的水力计算[1]上下游实测资料,通过公式(6)~公式(8)可求得渐扩式消力池综合绕流阻力系数实测值(见表1).

表1 综合阻力系数的比较
由公式(6)可知,渐扩式消力池综合绕流阻力系数CL是跃前断面弗劳德数Fr1、水跃共轭水深比η及跃后断面与跃前断面宽度比β的函数.由于实际工程中,水跃跃后条件往往是未知的,故笔者对张志恒[1]实测的综合绕流阻力系数重新整理分析,分析结果(见图2).由图2可知,相对综合绕流阻力系数β4CL是跃前断面弗劳德数Fr1的函数,并随着Fr1的增大而减小.对相对综合绕流阻力系数β4CL进行拟合,可得:
(9)
将式(7)和式(8)代入式(9),即可得渐扩式消力池综合绕流阻力系数CL的显示计算式,即:
(10)
将公式(10)计算的综合绕流阻力系数计算值列入表1,可知公式(10)的计算值与文献[1]中给出的实测值十分接近,公式(10)计算的综合绕流阻力系数平均误差仅为0.9%.
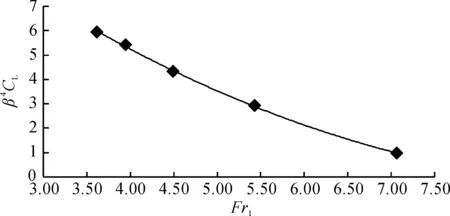
图2 相对综合绕流阻力系数随跃前断面弗劳德数的分布
2 渐扩散水跃跃后水深和水跃长度
公式(2)建立的平底矩形断面渠道渐扩散水跃动量方程公式求解水跃跃后水深,尚需知道跃后断面消力池宽度b2.由公式(8)可知,跃后断面消力池宽度b2是水跃旋滚长度Lr的函数.张志恒[1]虽给出了渐扩散消力池水跃旋滚长度Lr的计算公式,但其经验公式具有一定的局限性.
吴宇峰等[15]捕捉水跃旋滚区水体质点的运动规律,提出的渐扩式消力池水体质点的运动方程为:
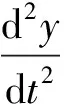
(11)
式中:t—水跃区水体质点从跃前断面往跃后断面运动的时间;
y—水体质点在t时间内在竖直方向上运动的距离;
f—消力池扩散角为零时,水体质点受压力差引起的质点竖直向上运动的加速度;
kθf—由于消力池边墙扩散额外引起的竖直向上运动加速度,k—额外加速度系数.吴宇峰等[15]假定的水体质点运动起点为跃前断面水流表面,认为水体质点从跃首运动到跃后断面的水平运动距离为水跃长度Lj,并假定水体质点运动至某一断面时的水平瞬时速度正比于该断面平均流速vx,即:
(12)
式中:x—水流沿主流方向的运动距离;
c—流速系数.同时假定tanθ=θ.
吴宇峰等[15]对公式(12)进行积分,得到水跃长度的表达式为:
(13)
1965年,RAJARATNM[16]就将水跃分为旋滚长度Lr和水跃长度Lj,旋滚长度是指跃首到水跃表面旋滚末端之间的水平距离,水跃长度是指跃首至跃后水深约等于尾水水深断面之间的水平距离.1984年,HUGHES[17]也将水跃长度分为旋滚长度和水跃长度,其定义与RAJARATNM相同,并认为水跃长度的定义与美国垦务局的BRADLEY和PETERKA水跃长度试验数据一致.
基于上述对水跃旋滚长度和水跃长度的认识,笔者认为水体质点,在从跃首表面运动到旋滚末端表面经过的水平距离应为水跃旋滚长度,同时不再假定tanθ=θ,则对公式(12)重新积分,可得:
(14)
(15)
式中A须通过试验确定.
根据张志恒[1]上下游实测资料,笔者将公式(15)计算的A重新进行分析,结果(见图3).对A进行拟合可得:
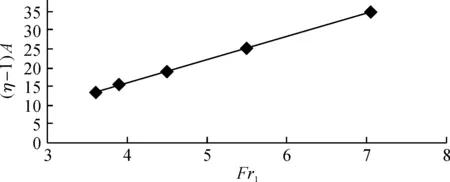
图3 A值分布
(η-1)A=6.108 3Fr1-8.401 7
(16)
公式(16)计算的平均误差为0.67%.将公式(16)代入公式(15),可得渐扩散消力池水跃旋滚长度的计算公式为:
(17)
将公式(6)进行变形,则:
(18)
将β=b2/b1=(b1+2Lrtanθ)/b1代入公式(18),可得:
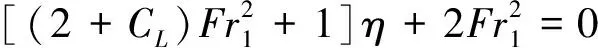
(19)
上式即为平底矩形断面渠道渐扩散水跃共轭水深比的计算公式.
通过公式(10)、公式(17)和公式(19)即可求解渐扩散水跃跃后水深和水跃旋滚长度.在求解计算时,可根据公式(10)先行计算综合绕流阻力系数CL,再将公式(17)计算的水跃旋滚长度函数关系式代入公式(19),借助Excel单变量求解功能,快速求解水跃共轭水深比及水跃旋滚长度.
3 公式的验证
根据张志恒[1]实测资料,用公式(10)、公式(17)和公式(19)计算所得的平底矩形断面渠道渐扩散水跃跃后水深和水跃旋滚长度计算值列入表1.由表1可知,用本文公式计算的跃后水深平均误差为0.21%,最大误差为0.39%;水跃旋滚长度平均误差为0.62%,最大误差为1.53%.
张志昌等[18]认为,应用传统方法计算渐扩散消力池时,边墙反力按梯形和1/2抛物线形计算的跃后水深效果较好,同时认为文献[12]提出的共轭水深拟合公式也具有较好的计算效果.为进一步验证公式(10)、公式(17)和公式(19)的适用性,笔者在文献[8]对上述3家公式比较的基础上,应用矩形扩散水跃的水力计算的上游实测数据,将公式(10)、公式(17)和公式(19)联合求解的跃后水深计算值与其余3家公式一同绘入图4.
由图4可知,公式(10)、公式(17)和公式(19)联合求解的跃后水深与其余3家公式均接近.在跃前断面弗劳德数3.5
本文在律定综合绕流阻力系数CL和相对加速度f/g和扩散角θ的函数A时,均采用矩形扩散水跃的水力计算[1]的试验数据(θ=5.711°),为分析公式(17)和公式(19)的通用性,拟用矩形扩散水跃的水力计算[1]的上游实测数据,改变边墙扩散角θ,对公式进行进一步的分析.在实际工程中,边墙扩散角θ通常较小,一般要求θ<12°,本文计算取θ=12°.文献[19]认为边墙反力按梯形计算,其渐扩散水跃跃后水深公式在较大边墙扩散角下也能获得较好的计算效果.将梯形公式和公式(19)计算的渐扩散水跃共轭水深值绘入图5.由图5可知,在较大边墙扩散角θ=12°时,本文计算的共轭水深比与梯形公式计算值十分相近.在3.5 图4 各公式计算的跃后水深[8] 图5 跃后水深的比较(θ=12°) 由上可知,在跃前断面弗劳德数3.5 本文将水流边界层脱壁而产生绕流阻力的理论应用到渐扩式消力池中,用以求解平底矩形断面渠道渐扩散水跃跃后水深.研究表明,渐扩散水跃综合绕流阻力系数是跃前断面弗劳德数、水跃共轭水深比及水跃旋滚末端断面和水跃跃前断面宽度比的函数.相对综合绕流阻力系数是跃前断面弗劳德数的函数.本文作者根据绕流阻力假定和吴宇峰[15]的渐扩散水跃跃长的研究中关于平底矩形断面渠道渐扩散水跃水体质点的运动方程,分别得出了渐扩式水跃跃后水深和水跃旋滚长度新的计算公式.根据张志恒的实测资料,用公式(10)、公式(18)和公式(20)计算所得的渐扩散水跃跃后水深和水跃旋滚长度平均误差分别为0.21%和0.62%,并用已有渐扩散水跃计算公式对其适用性及通用性进行了验证.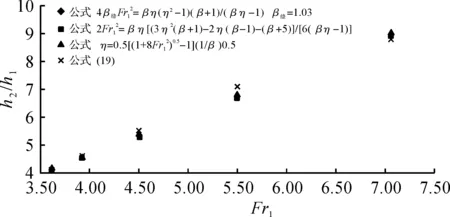

4 总 结

