储能用锂离子电池动态阻抗模型及其特征参数研究

许守平 胡 娟 侯朝勇



储能用锂离子电池动态阻抗模型及其特征参数研究

许守平 胡 娟 侯朝勇

（新能源与储能运行控制国家重点实验室，中国电力科学研究院有限公司，北京 100192）

为了能更加准确地判断锂离子电池的动态一致性，本文利用电化学阻抗谱作为电池外特性和内特性的联系纽带，旨在通过交流阻抗谱的测试手段来开展锂离子电池动态阻抗模型的研究。通过电化学阻抗谱测试实验，基于最小二乘法并根据实验数据对电池动态阻抗模型参数进行识别，得到锂离子电池的动态阻抗模型。试验表明，该方法所提取的锂离子电池动态阻抗模型能很好的满足储能试验的要求，具有很高的精度，可作为锂离子电池组一致性判断的依据。

锂离子电池；动态阻抗；最小二乘法；特征参数

锂离子电池因自身优点，作为主流的储能形式已广泛应用于电力系统，但为满足电压和能量要求，需要将成千上万的单体锂离子电池串并联起来构成电池组来进行工作[1-2]。随着电池储能系统长时间的充放电循环，单体电池的各项参数会发生变化，电池之间差异化明显，影响电池组的安全稳定运行，降低储能系统的可利用容量，缩短其使用寿命。因此，为了能更准确地把握电池组在充放电过程中的一致性，需要对电池一致性状况实时进行判断和管理，而电池动态阻抗是判断电池动态一致性的重要表征量之一[3]。建立电池动态阻抗相对应的等效电路模型，提取与动态一致性相关的特征参数，可实时在线地对电池进行智能管理，提高电池的容量利用率和使用寿命。

目前，国内外很多高校和科研机构都在开展电池动态阻抗模型和其特征参数的分析研究工作。国内的清华大学、哈尔滨工业大学、北京交通大学等著名高校的研究者从锂电池的电化学模型入手，通过对电池内部结构及工作原理的分析，结合电极动力学原理，构建电极等效电路，建立了电池静态阻抗模型[4-8]。日本、美国的科研院所通过设计电路来分析锂离子电池中各项扩散参数的变化，在电化学阻抗谱中对实验数据和拟合数据进行了对比，可以达到很高的精度来模拟电化学反映体系[9-10]。总的来说，虽然国内外的研究学者都已认识到构建锂电池动态阻抗模型的重要意义，但由于锂电池在工作时反应机理比较复杂，很难用绝对有效的方法完全反应电池内部的物理化学过程，因此锂电池动态阻抗模型的建立仍旧是锂电池在线管理的重要难点之一。本文从锂电池工作过程的电极极化现象出发，根据锂电池在充放电过程中的动态特征，通过大量历史的测试数据积累，构建出与测试电池相匹配的动态阻抗等效模型，并根据实验数据对动态阻抗模型的特征参数进行识别，对所得出的电路模型进行不断修正，来反映锂电池的动态特征，为锂电池的动态在线管理策略提供有效的支撑。

1 锂离子电池的动态阻抗及简单模型

1.1 锂离子电池动态阻抗

通常，采用电化学阻抗谱测量电池阻抗是基于电池处于静置状态下进行的。但储能系统在实际运行中，电池少有条件处于完全静置的状态下，因此，研究实时在线的电池阻抗变化对于判断电池动态一致性非常必要。电池动态阻抗可以理解为对于一组同批量生产的同类型电池，在充放电过程中，当分别给这组电池施加同一个扰动信号，在输出侧得到的一组阻抗响应信号；如果这些响应信号一致性很高，就可认为这组电池具有很好的动态一致性。所以，电池的动态阻抗也可表示为电池在充放电过程中，体现电极极化现象，反映电极动力学特征及电池一致性的阻抗。

1.2 锂离子电池的简单阻抗模型

根据国内外研究成果，目前比较公认的锂离子电池电极系统的阻抗模型如图1所示[3,11]。

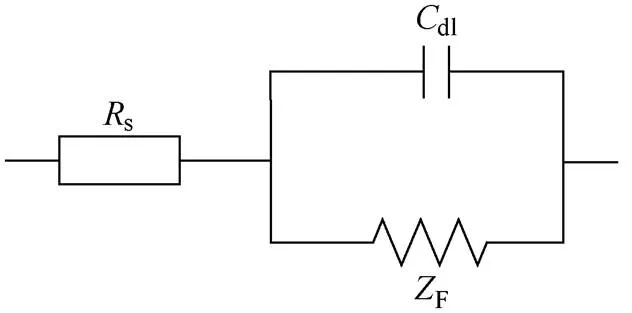
图1 电极系统阻抗模型示意图

其中，s表示溶液电阻；dl表示电极与电解质溶液两相之间的电双层电容；F表示法拉第阻抗。可以得到电池的阻抗表达式为

其中，F为法拉第导纳。当电池进行电极反应时，若其他条件不变，法拉第电流密度F是一个多元函数，其中的自变量包括电极电位、电极表面的状态变量X以及影响电极反应速度的反应粒子在电极表面处的活度C：

若给电极系统施加一个电位扰动，使得变为+D，则在满足阻纳因果性条件时，变量X、C也会产生一个相应的改变量DX和DC，使得函数F也会产生改变量DF。如果用t表示法拉第电流受电极电位变化的影响，则有

式中，t为电荷转移电阻。

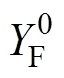
由于锂离子电池的电极是平面电极，对于恒温下静置溶液中扩散的分子或离子来说，可以认为是厚度无限的“滞流层”所对应的半无限扩散过程，此时，因阳极电流和阴极电流的不同而不同。当该电流是阳极电流时，即当=0时，则有

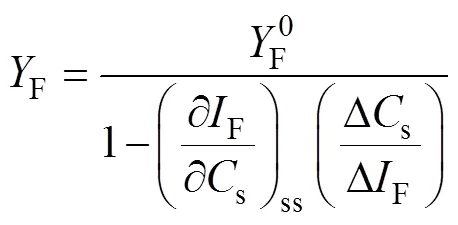
将法拉第导纳转换为阻抗的形式：

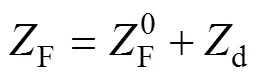
利用欧拉公式将上式转化为

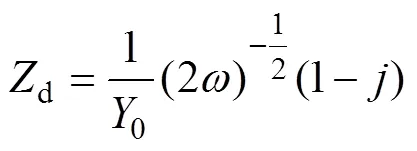
d表示界面阻抗，若只有电极电位和反应物浓度s影响电极过程，则此时0为

式中，为化学计量系数；为法拉第常数；s为电极表面活度；是扩散系数；g为反应物反应级数。从式（7）看出，扩散过程所对应的阻抗在复平面图中位于第一象限，实部和虚部的数值相同，呈现一条45°倾斜的直线，可以用W表示，也可称为扩散阻抗。0作为表征W数值大小的特征参数，能反映出W随变化的情况。

2 电化学阻抗谱的测量

结合电池阻抗基本模型，对电池进行初步的阻抗谱测量，根据测试数据，可以对基本模型进行修正，得到较为准确的电池阻抗等效模型。本文选用的锂电池为LiFePO4储能电池，标称容量为20Ah，额定工作电压3.2V，测试在1个标准大气压下，温度为20℃的恒温实验室进行。测试过程是在对LiFePO4储能电池充放电的同时进行动态阻抗谱测试，将不同频率扰动信号同时作用到电池输入端，在输出侧可以获得不同频率点所对应的响应信号，其测试时长由最低频率来决定，能在较短的同一时间内获得各个频率区段交流阻抗的特征和各个频率点的阻抗值，从而分别测量到充电和放电过程中电池在不同下的阻抗谱。整个测试系统的电路接线图如图2所示。

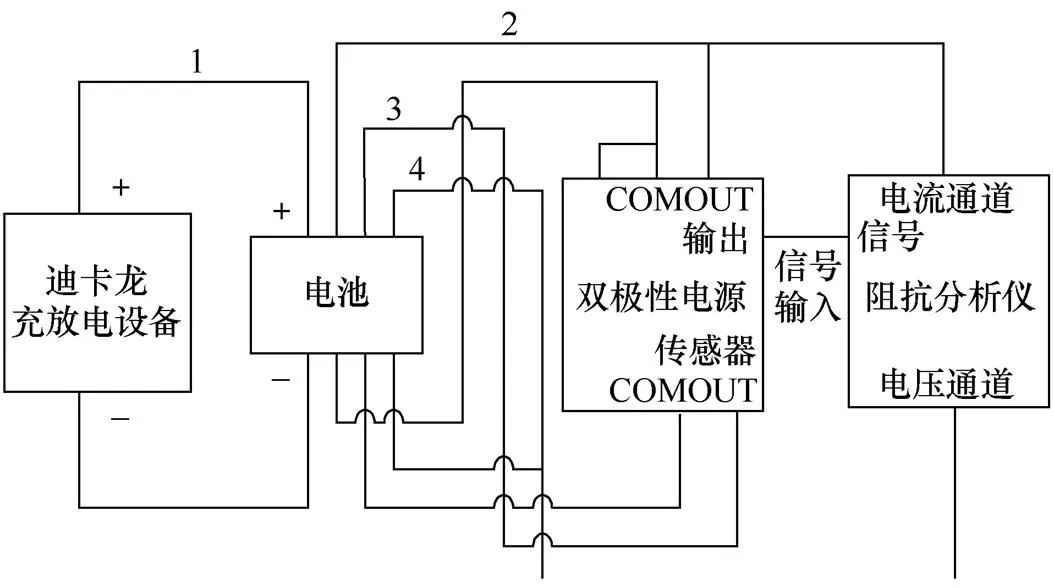
图2 测试系统电路接线图

为了研究电池在充放电过程中电化学阻抗谱的变化情况，并根据不同频率下测试所获得的阻抗数据来提取出与电池动态特性相关的特征参数，对样品电池进行不同倍率下的充放电循环测试，每达到一定的循环周期，进行容量标定后，再分别进行一组完整的充电和放电过程的阻抗谱测试。测试时，电池在恒流充放电模式下进行循环寿命测试，充放电倍率分别为0.2、0.5、1。每经过50次循环后，对电池进行容量的标定，假定标定容量结果为a，根据a将全区间平均分为20个区段，如图3所示，计算出完成每个区间段的充放电所需要的时间1，在每个区间内中点附近进行交流阻抗谱的测试，保证阻抗谱测试时长2＜1，这样可以近似认为测量所获得的阻抗谱数据是电池处于某状态下的阻抗数据，能反映当前状态下电池动态阻抗的特征。

图3 全SOC区间的划分及测量时间示意图

由于测试承接在标定容量测试之后，以充电过程为例，此时可认为当前电池的为0。动态交流阻抗谱测试步骤总结如下：

1）以以0为起点，每个区间段内进行恒流充电，时长为1。

2）在步骤1）中的每个区间内充电时长达到(1-2)/2时，开始进行动态交流阻抗谱测试，时长为2。

3）重复步骤1）至步骤2）20次，完成所有区间段的阻抗谱测量，停止测试。

同样的，放电过程的测试与充电过程类似，测试起点选为=100%。

测试后，可以得到不同状态下的交流阻抗谱，通过后期对实验数据的拟合可以提取出特征参数，从而寻找出特征参数随变化的规律。

3 锂离子电池动态阻抗模型

基于电池的基本动态阻抗模型和阻抗谱的测试数据，可以对基本模型进行修正，得到电池的动态阻抗等效电路，电路中主要包括溶液电阻s，电双层电容dl，电荷传递电阻ct，扩散阻抗w。从实验结果可以观察到，阻抗谱在高频区是一条位于第四象限的曲线，垂直交于横轴，交点代表了s参数值的大小，中频区是位于第一象限的半圆，圆心在横轴附近，这是由dl与ct并联回路引起的，而低频区是一条与横轴成45°的直线，这代表了电极反应中带电粒子在固相中的扩散过程，对应的等效元件即为扩散阻抗w。事实上，由于在阻抗谱中存在第四象限的曲线，即阻抗在高频区呈现出感抗的特征，因此，必须把电感考虑到等效电路中来，经研究表明，电池体系出现感抗的作用并非是产生了感应电流，而是与电极的多孔性结构、表面不均匀以及连接引线有关[11]。因此，在溶液电阻s前面串联一个电感来等效这部分阻抗谱的特征。此外，从实验结果中还可以观察到，阻抗谱中间的半圆存在一定的变形，弧长对应的圆心角没有达到p，并且圆弧对应的圆心并不一定在横轴上，因此这里的电双层电容不是一个纯电容，可以考虑用常相位元件来代替电双层电容，因此可得到如图4所示的修正等效电路模型。

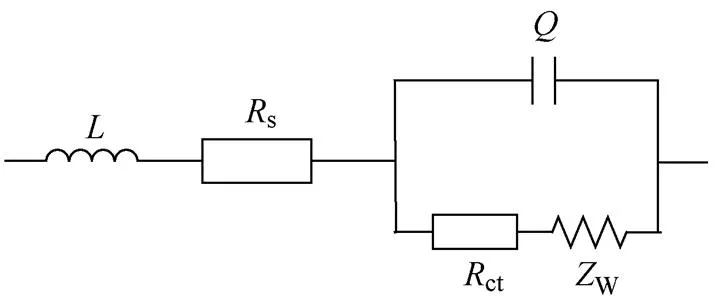
图4 修正后的等效电路模型

4 动态阻抗模型的特征参数识别

在图4中的等效电路模型中包含了简单和复合的等效元件，其中一些元件的参数正是反映动态阻抗一致性的特征参数，可以将不同特征参数结合实际阻抗谱的曲线特征进行划分并提取出来，明确阻抗谱中的每一部分代表的电化学结构和基本单元步骤，并用特征参数来表征其物理意义，通过将特定频率范围内的多个阻抗数据利用最小二乘法进行曲线拟合，从而求取特征参数值。

将阻抗谱进行频率区间划分，根据曲线特征选取阻抗数据利用非线性最小二乘法来拟合测试曲线，通过曲线的几何特征提取出特征参数。以中频段的圆弧拟合作为例子进行介绍。此处的动态阻抗表达式简化为

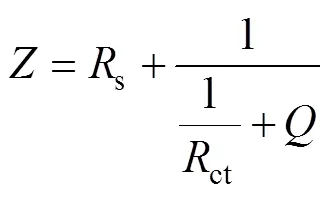
通过对圆弧的拟合，将其中的Rs和Rct两特征参数提取出来，圆弧拟合的几何关系图如图5所示。

若定义为拟合点与实验数据点之间误差的平方和，则如式（11）所示：

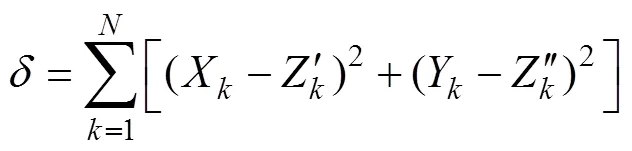
如果把式（10）带入式（11），可以得到一个误差平方和关于0、0、0的多元函数，根据最小二乘法的原理，欲获得最佳的拟合曲线，需要保证取最小值，则根据多元函数求极值的方法可分别对求关于0、0、0的一阶偏导数并令导数值为0，构成线性方程组并求解可得到待定系数0、0、0。

根据线性方程组求得半圆的圆心（0,0），和半径0之后，可依据图5中的几何关系求得特征参数s和ct，表达式如下：

然后利用仿真软件对实验阻抗数据进行阻抗谱拟合，从而提取出与动态阻抗相关的特征参数。经过多次迭代，得到拟合后的阻抗谱如图6所示，同时还获得等效电路中各元件的参数值见表1。这样就可以得到较为准确的样品电池等效电路模型。

表1 等效电路各元件参数值

整个测试周期主要包括容量标定测试和动态交流阻抗谱测试两个部分，以1恒流充放电为例，整个测试周期大约需要4h，主要是容量标定要占用大量时间，而实际阻抗谱测量则很快。在实际在线化应用中，为了减少避免电池在不同频率下的阻抗测试的延时误差，可以考虑对电池阻抗影响较大的频率段进行测试，而不用全频率扫描，一般选用100Hz～10kHz的频率区间进行，这样可以在很短的时间内完成电池在某个点的动态阻抗的测量，给电池管理提供很有利的管理依据。

5 结论

本文在现有阻抗模型的基础上，采用电化学阻抗谱测量的手段来提取相关的特征参数，通过这种连接电池内外特性的阻抗谱测试手段来寻找特征参数随变化的一般规律，基于最小二乘法通过提取的特征参数来对电池动态阻抗模型参数进行识别，试验表明，该方法所提取的锂离子电池动态阻抗模型能很好的满足储能试验的要求，具有很高的精度，可作为锂离子电池组一致性判断的依据。但阻抗谱的测试仍处于实验室阶段进行，还不能达到在线化测试的水平，所以下一步可以考虑开展锂离子电池组在实际运行环境下的阻抗谱测试，从而实现电池组动态一性在线判断的目的。

[1] 胡娟, 杨水丽, 侯朝勇, 等. 规模化储能技术典型示范应用的现状分析与启示[J]. 电网技术, 2015, 39(4): 879-885.

[2] 王建宝, 巫卿, 王瑾, 等. 储能技术在风光发电系统中的应用[J]. 电气技术, 2013, 14(9): 91-93.

[3] 时玮. 动力锂离子电池组寿命影响因素及测试方法研究[D]. 北京: 北京交通大学, 2014.

[4] 席安静. 磷酸铁锂电池电化学阻抗谱实验研究[D]. 北京: 清华大学, 2012.

[5] 徐睿. 锂离子电池劣化程度与阻抗模型相关性研究[D]. 哈尔滨: 哈尔滨理工大学, 2010.

[6] 张彩萍, 姜久春, 张维戈, 等. 梯次利用锂离子电池电化学阻抗模型及特性参数分析[J]. 电力系统自动化, 2013, 37(1): 54-58.

[7] 牛利勇, 时玮, 姜久春, 等. 纯电动汽车用磷酸铁锂电池的模型参数分析[J]. 汽车工程, 2013, 35(2): 127-132.

[8] 张文华, 吴三毛, 刘平, 等. C/LiFePO4动力电池电化学交流阻抗谱的研究[J]. 电源技术, 2015, 39(9): 1838-1842.

[9] Sadri M, Shoulaie A. A practical approach to measure battery's internal impedance[C]//Power Electronic & Drive Systems & Technologies Conference. IEEE, 2010: 418-422.

[10] Osaka T, Momma T, Mukoyama D, et al. Proposal of novel equivalent circuit for electrochemical impedance analysis of commercially available Lithium ion battery[J]. Journal of Power Sources, 2012, 205(14): 483-486.

[11] 张文华, 裴锋, 刘平, 等. 磷酸铁锂电池循环过程中电化学交流阻抗研究[J]. 电源技术, 2015, 39(1): 54-57.

Study on the dynamic impedance model and characteristic parameters of lithium ion battery for energy storage system

Xu Shouping Hu Juan Hou Chaoyong

(State Key Laboratory of Operation and Control of Renewable Energy & Storage Systems, China Electric Power Research Institute Limited Company, Beijing 100192)

In order to more accurately determine dynamic consistency of lithium ion battery, this paper using electrochemical impedance spectroscopy as a battery features and characteristics of bond, by ac impedance spectroscopy testing method to carry out to study the dynamic consistency of lithium ion batteries. In electrochemical impedance spectrum test experiment, the dynamic impedance model of lithium ion battery is identified based on the least square method and the experimental data. The test shows that the dynamic impedance model of lithium ion battery extracted by this method can meet the requirements of energy storage test well, and has high precision. It can be as a basis for the dynamic consistency judgment for lithium ion batteries pack.

lithium-ion batteries; the dynamic impedance; least square method; characteristic parameters

2018-03-26

国家重点专项（100MWh级新型锂电池规模储能技术开发及应：2016YFB0901700）

国家电网公司科技项目（新一代电池管理系统关键技术研究：DG71-16-018）