大悬臂预应力混凝土倒T盖梁设计与施工过程分析研究

李建强，孙立山

（1.上海市政工程设计研究总院集团广东有限公司，广东 佛山 528200；2.中交第一航务工程局第四工程有限公司,天津市 519000）

0 引言

城市桥梁设计过程中，城市高架桥通常需要在桥上有足够的行车道宽度。同时，为了减小桥梁对桥下道路通行的影响，需最大限度地减少占地面积。但是，在这种情况下容易产生桥面宽度大于下部结构横向尺寸的矛盾。大悬臂预应力混凝土盖梁比较完美地解决了这一问题，因此成为城市桥梁设计的优选方案[1-2]。但构件悬臂长度的增大必须配合梁截面高度的增加，并且伴随着构件内力急剧增加。受力模式的改变、跨高比的减小，使得构件受力演变为深弯构件[3]。城市桥梁施工过程中，为了协调道路边通行边施工需求，往往存在非对称架梁施工，而设计师通常根据规范《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）采用简化的简支梁或连续梁[4]，利用平面杆系单元建立刚架模型来计算大悬臂盖梁结构[5-6]。但是，大悬臂预应力盖梁具有很明显的空间效应，传统的杆系结构无法有效计算出施工阶段盖梁受力情况，不能有效考虑到深梁结构受力特性。文章结合某工程中采用的大悬臂预应力倒T盖梁，对该类型盖梁的设计思路、设计方法以及在施工阶段盖梁受力情况进行探讨分析。

1 设计概况

1.1 技术标准

（1）道路等级：一级公路技术标准；

（2）设计车速：80 km/h；

（3）净空要求：主线桥下地面辅路净空不小于5.0 m；

桥梁标准横断面如图1所示。

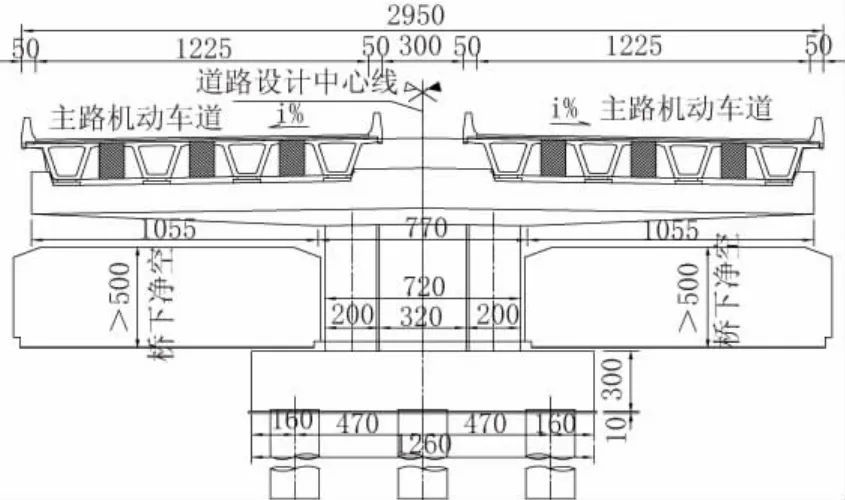
图1 桥梁设计横断面（单位：cm）

1.2 工程概况

1.2.1 结构设计

某工程为了满足通行要求，桥面设计双向6车道，桥下双向4车道。上部结构横断面确定后，确定盖梁的长度为28.8 m。考虑到两侧桥底地面车辆通行净空、净宽，故高架桥路线采用预应力大悬臂盖梁方案，墩顶负弯矩控制设计方案。通过初步试算确定盖梁中心（墩顶处）高度为4.3 m，端部（悬臂处）高3.5 m，两墩柱中心间距为5.2 m，两侧各悬臂10.55 m，盖梁中心到端部采用直线过渡。上述盖梁尺寸满足桥下净空、净宽要求，墩顶满足负弯矩受力要求，端部尺寸满足抗剪、抗弯要求。综合结构受力、施工、钢筋布置构造等要求，考虑到城市景观效果，盖梁顺桥向宽为3.5 m。文章选取该项目中A3c型盖梁进行研究，按照A类预应力混凝土构件设计，混凝土等级为C50。根据盖梁受力的弯矩分布，共布置12束Φs15.2-15的低松弛高强钢绞线预应力钢束，盖梁中心线对称布置，共N1、N2、N3和N4四种形状，每种3束，每束15根，分两次张拉，锚下张拉控制应力σcon=0.75 fpk=1 395 MPa。具体盖梁构造及钢束形状如图2所示。

图2 桥墩盖梁构造及钢束布置图（单位：cm）

1.2.2 结构施工过程

（1）浇筑C40桥墩及C50盖梁混凝土，混凝土强度达到95%强度值时张拉第一批钢束（N2和N4）。

（2）架梁。原设计左右对称架梁，现由于现场条件存在部分跨径单幅架梁情况（桥下范围单向双车道通车，部分跨径两幅桥中间有高压线塔）。

（3）张拉第二批钢束（N1和N3），浇筑湿接缝和二期施工。

（4）成桥，运营。

2 空间有限元模型及受力分析

2.1 三维实体有限元模型建立

利用有限元细部分析软件Midas/FEA建立模型。

（1）实体模型：采用映射方式建立空间规则六面体单元模型。

（2）预应力钢束与普通钢筋：利用二维样条曲线网格模拟，按照自动就近节点耦合的方式使其与混凝土实体单元节点连接并形成“变形协调”。

（3）边界条件：假定桥墩盖梁结构桥墩底面完全固结。

（4）荷载：模型计算荷载考虑预应力、活载、自重、上部恒载及整体升降温。

2.2 空间受力分析

根据设计图纸建立Midas/Civil空间梁单元模型及Midas/FEA实体单元模型。重点分析施工阶段1（张拉第一批钢束）、施工阶段2（原设计对称架梁和现存在部分跨径单幅架梁）及运营阶段4的受力情况。按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)进行荷载组合后，选取施工阶段及运营阶段最不利的荷载工况进行结果分析。

2.2.1 施工阶段1分析

施工阶段中，张拉第一批预应力钢束后，按照规范组合工况考虑恒载与预应力荷载，且荷载组合系数为1。施工阶段盖梁实体模型正应力分布如图3所示，主应力分布如图4所示，空间梁单元模型及实体单元模型正应力结果对比见表1。

图3 施工阶段1盖梁结构正应力（单位：MPa）

图4 施工阶段1盖梁结构主应力（单位：MPa）

表1 施工阶段1两种盖梁结构模型结果对比 MPa

在施工阶段1中，由图3知，在盖梁结构上部分正应力最值为-4.31 MPa和端部+0.63 MPa，盖梁结构下部分区域处于受压状态，正应力（压应力）最值为-15.42 MPa（此处为钢束锚固点，存在应力集中），忽略钢束锚固区，盖梁结构下部分区域正应力的最值为-3.06 MPa。在墩柱与盖梁结合部分为正应力（拉应力）最值为+0.92 MPa；满足规范≤0.7 fpk=+1.855 MPa。由图4知，盖梁主应力最值分别为-0.38 MPa和+2.97 MPa（此处为钢束锚固点，存在应力集中），忽略钢束锚固区，盖梁结构主拉应力的最值为+0.92 MPa。盖梁与墩柱结合处主应力为+0.79 MPa。均满足规范≤0.7 fpk=+1.680 MPa。

2.2.2 施工阶段2分析

施工阶段中，按照规范组合工况考虑恒载、预应力荷载和小箱梁恒载，且荷载组合系数为1，原设计左右对称架梁，施工阶段盖梁实体模型正应力分布图如图5所示，盖梁处于受压状态，正应力值为-3.15 MPa（忽略盖梁钢束锚固端应力集中），墩柱与盖梁结合处正应力最值为+0.38 MPa。主应力分布如图6所示，盖梁与墩柱结合处主应力最值为+0.68 MPa。均满足规范。现由于现场条件，存在盖梁单幅架梁，此时施工阶段盖梁实体模型正应力分布图如图7所示，墩柱与盖梁结合处正应力最值为+1.19 MPa，满足规范限值。主应力分布如图8所示，墩柱与盖梁结合处主应力最值为+1.886 MPa，超过规范限值0.7 fpk=+1.680。

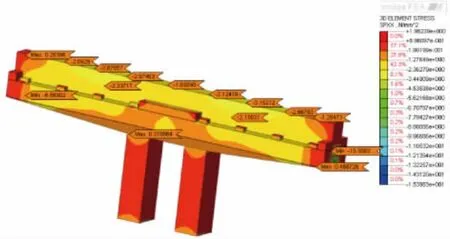
图5 施工阶段2盖梁结构正应力（对称架梁）（单位：MPa）

图6 施工阶段2盖梁结构主应力（对称架梁）（单位：MPa）

图7 施工阶段2盖梁结构正应力（单幅架梁）（单位：MPa）

图8 施工阶段2盖梁结构主应力（单幅架梁）（单位：MPa）

为判断墩柱与盖梁结合处混凝土开裂程度，需分析梁墩交界处混凝土主应力分布情况，从梁墩交界处分别向上3 cm处、向下3 cm处，从外向内分三层，分别为表面距离表面3 cm处、距离表面12 cm处和距离表面25 cm处各单元节点应力的大小变化情况，如图9所示。

由图 9（a）（b）知，在墩柱与盖梁结合处，表面节点主应力最值达到+1.89 MPa大于混凝土强度设计值ftk=+1.65 MPa，距墩柱与盖梁结合表面3 cm、12 cm和25 cm处，主应力都趋于+1.5 MPa、+1.0 MPa 和 +0.5 MPa；由图 12（c）（d）知，距墩柱与盖梁结合位置3 cm处，主应力值小于+1 MPa，满足规范限值。因此，在单幅架梁过程中，为了避免单幅架梁过程中在盖梁与墩柱结合处出现裂纹，建议：（1）在盖梁另外一侧加配重；（2）加强配筋，墩柱受力主筋伸入盖梁长度≥30d；（3）在墩柱与盖梁结合处增设钢筋网片，防止表面混凝土开裂。

2.2.3 运营阶段分析

结构运营阶段分析采用最不利荷载组合：1.2×恒载＋1.4×一侧活载＋1.4×0.7×整体升温。以线弹性理论为基础的材料弹性阶段分析，结构在运营阶段正应力如图10所示，除盖梁端局部存在最值为+0.33 MPa拉应力和下缘与墩柱结合区域存在+0.92 MPa拉应力外，整个盖梁处于受压状态，最值为-6.40 MPa，墩柱与盖梁结合处，正应力最值为+0.91 MPa，均满足规范限制。但是，混凝土结构在极限状态下会表现出材料非线性特性，构件设计时需要考虑构件的弹塑性承载力，所以仅仅做线弹性分析不能完全反映结构的真实应力状态。在盖梁顶植入2排32@150普通钢筋，考虑盖梁顶普通钢筋作用和混凝土的非线性，本构模型选取总应变裂缝，混凝土张拉函数选取理想破坏模型。盖梁结构在荷载系数为1.0时，盖梁结构处于弹性、塑性区域位置见图11。由图11知，盖梁结构仅在钢束锚固端以及支座的局部位置处结构材料进入了塑性状态。建议在此处加大配筋，防止混凝土开裂。选取盖梁端部分析裂纹可能开展的位置处的裂缝法向应力大小，用圆形标记发生裂纹的位置，圆片的法向就是开裂方向，圆的大小代表裂缝的大小。最值为+1.6 MPa（见图12）。建议在此位置处根据法向应力的大小和方向，合理配筋。

图9 墩柱与盖梁结合处外表面及梁内混凝土主应力分布情况

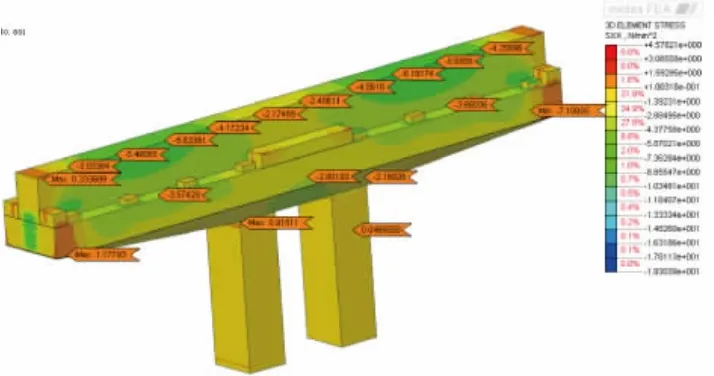
图10 运营阶段4盖梁结构正应力（弹性模型）（单位：MPa）

图11 运营阶段4盖梁结构弹塑性状态位置分布（非线性模型）（单位：MPa）

图12 塑性阶段裂缝开裂位置处的裂缝法向应力（非线性模型）（单位：MPa）

3 结论

通过对大预应力悬臂倒T盖梁空间受力实体和梁单元模型分析对比，相关结论为：

（1）对于大挑臂预应力倒T盖梁，实体模型及梁单元模型计算结构应力分布总体相同，但略有差异，主要表现在局部应力集中处，如墩柱柱顶、墩柱与盖梁结合处以及盖梁端部，因在墩顶处盖梁模型不满足平截面假定以及小变形假定，无法对局部应力有效分析和配筋，因此对于此类大悬臂盖梁有必要进行实体模型分析；

（2）对于此类盖梁设计，不能仅仅考虑成桥运营阶段的分析，施工阶段分析和施工顺序是此结构设计及分析的重点；

（3）对于此类盖梁施工过程中的架梁方式，建议采用对称架梁，如特殊原因存在单幅架梁，建议在盖梁另外一侧配重，保证施工安全；

（4）在施工过程中，在墩柱与盖梁结合处，墩顶盖梁段截面横向受力不符合平截面假定，出现局部应力集中现象比较明显，设计中应充分考虑此现象以减少盖梁的局部裂纹，提高结构耐久性。