铁路钢桁梁斜拉桥斜拉索张拉力的计算方法研究

胡怡然

（中铁二院重庆勘察设计研究院有限责任公司，重庆市 400023）

0 引言

铁路钢桁梁斜拉桥通常采用悬臂施工，设计过程中分两步走：首先确定合理的成桥受力状态（即目标受力状态），进而确定施工过程受力状态。本文旨在探讨合理的成桥受力状态下如何确定施工过程受力状态。

合理的施工过程受力状态应考虑两方面因素：一是施工过程中桥梁受力安全，二是施工完成时与目标受力状态吻合良好。在斜拉桥成桥状态确定的前提下，桥梁各部位结构尺寸及斜拉索索力亦已明确，主要施工步骤可根据施工条件大致确定。施工过程中斜拉索的张拉力是控制施工过程受力状态的重要因素，因此合理的斜拉索张拉力对于确定施工过程受力状态至关重要。

施工过程受力状态的计算方法通常有正装-倒拆迭代法、倒拆法、无应力控制法和正装迭代法等[1]。前3种方法基于合理的成桥受力状态进行倒装计算，均存在不同程度的不闭合问题。正装迭代法则按如下思路进行：先假定1组张拉力，按照既定的施工步骤对桥梁进行正装计算，将计算所得桥梁受力状态与确定的合理成桥状态进行比较，根据两者差值情况调整拟定张拉力，直至桥梁受力状态与确定的合理成桥状态基本接近[1-2]。计算过程中引入差分法可使拉张力的拟定值更直接、更有效。

为简化施工工序及缩短施工工期，许多公路斜拉桥均采用斜拉索一次张拉到位，即斜拉索在安装过程中张拉一次，施工完成时桥梁受力状态达到合理成桥状态[3-4]。铁路斜拉桥二期恒载在恒载中所占比例较大，如斜拉索采用一次张拉到位的施工方案，则施工过程中由于斜拉索张拉引起的主梁下缘拉应力过大，不利于桥梁受力，本文因此提出施工过程中各斜拉索张拉两次，即：悬臂施工阶段安装每根斜拉索时进行初次张拉，铺装二恒后各索再进行第二次张拉（即终张调索）。以某铁路钢桁梁斜拉桥为算例，对斜拉索施工过程张拉力的计算方法进行研究。

1 计算思路

1.1 悬臂拼装施工阶段

钢桁梁悬拼过程中，斜拉索仅安装时张拉，其张拉力按钢桁梁悬拼过程及合龙后受力安全、保持基本梁平塔直的原则确定。

1.2 合龙后施工阶段

斜拉索在铺装二恒后进行一次调整，使桥梁在成桥时处于合理的目标成桥受力状态，成桥状态索力与目标索力基本吻合。斜拉索均按一次张拉就位控制，即全部斜拉索按设定顺序张拉完毕后，桥梁的线形、斜拉索索力都达到目标值，各构件均满足受力要求。斜拉索终张根据索号按先偶数号后奇数号的顺序进行，张拉过程中桥梁的线形、受力状态和斜拉索索力不断地改变。该阶段的研究思路是：

（1）以设计所确定的合理成桥状态时的索力作为指导，按拟定的施工工序正装迭代确定斜拉索的张拉值。

（2）按步骤（1）所确定的终张力正装计算，检查终张调索过程及成桥时桥梁线型、受力情况和索力变化，以核实桥梁结构受力是否合理与安全。

2 计算方法

2.1 悬臂拼装施工阶段

桥梁结构施工总响应值是将各阶段响应值线性叠加而成。斜拉桥悬拼施工阶段如各施工工序已明确，则因恒载而发生的位移也是明确的，由斜拉索初张力引起的位移则随其值调整而变化，故可建立关于主桁节点的位移影响矩阵，用于确定斜拉索张拉力。计算简图如图1所示。

悬拼过程中各节段恒载影响早于其施工构件的受力及线形。令恒载作用节段j致节点i产生挠度Δij，那么恒载作用节点总挠度为：

同理，斜拉索初张力作用仅使早于其施工的桁段上挠值产生变化，令索j初张力为Tj,节点i在单位索力作用下产生上挠值δij，那么各点在初张力作用下的总上挠值为Δi’为：

根据第1节中所述的原则，确定各点的目标线形{ω}，从而建立位移影响矩阵方程如下：

式（3）可简写成式（4）所示的形式：

式中：[δ]为位移矩阵；{T}为初张力；{ω}为主桁节点目标位移；{Δ}为施工过程中主桁各节点在恒载作用下的挠度。

通过式（4）可得{T}，即为悬拼阶段各拉索的张拉力。

试算法可确定斜拉索初张力。具体可按如下步骤进行：

（1）根据斜拉索的计算理论，斜拉索一般承担其附近两节间各一半的恒载；根据该恒载的质量、斜拉索的角度反算斜拉索轴力作为第1组试算张拉力。

（2）以式（1）为基础，计算悬拼过程各节点挠度{Δ}。

（3）建立斜拉索张拉力对位移影响矩阵：把初张力输进电算程序计算内力，得到拉索张拉时主桁节点位移。张拉j号索，则i点产生的位移ωj与张拉力Tj之比值即为j号拉索单位索力对应j点位移的影响系数，可用δij=ωij/Tj表示。

（4）将[δ]和{Δ}代入式（4），且根据上述原则，明确各节点目标位移{ω}，解式（4），即可得斜拉索初张力{T}。

（5）把按上述步骤计算得到的斜拉索张拉力按拟定的施工方案正装计算，核实施工过程中桥梁结构受力是否满足规范要求，如结论是肯定的则可将该张拉力作为设计张拉力，如不满足则根据计算结果局部调整目标位移，重复步骤（1）～（4）的计算，直到满足要求为止。

2.2 合龙后施工阶段

合龙后终张按先偶数号索后奇数号索的顺序，先短后长；桥塔两侧对应拉索同时张拉，但终张索力根据计算有所不同。

终张索力按正装迭代法计算确定，先拟定张拉力，按上述施工顺序正装计算，得到成桥状态，将成桥索力与目标成桥索力[T0]相减，差值与拟定的张拉力相加后作为1组新的拟定张拉力，重新进行正装计算；按该流程反复计算，直至成桥索力与目标索力基本相同。为避免初始拟定索力的盲目性，可将目标成桥索力作为初始拟定索力，以加快收敛速度。

具体按如下步骤进行：

（1）初始拟定张拉力[F0]=[T0]，按既定施工工序计算得到成桥状态索力[F1]。

（3）将满足收敛精度要求的张拉力[F0]代入计算模型，重新进行正装计算，核查桥梁施工过程中的结构受力是否满足规范要求，结论如为肯定则将[F0]作为终张的张拉力；如结果是否定的，则可调整施工方案等方法，重复上述计算，直至可行。

3 计算方法验证

以某铁路钢桁梁斜拉桥（其半跨立面布置见图1）工程为例，验证本文所提出的计算方法。

3.1 索力与目标索力吻合情况

通过计算发现，成桥状态索力与目标索力吻合良好，误差控制在2‰以内，详见表1。

表1 成桥状态索力与目标索力对比表

3.2 悬臂拼装施工阶段桥梁受力情况

悬臂拼装施工过程中的桥梁受力情况见图2～5。由图中数据可知：桥梁受力安全。

图2 悬臂施工过程中下弦杆竖向位移图

图3 悬臂施工过程中主塔顺桥向位移图

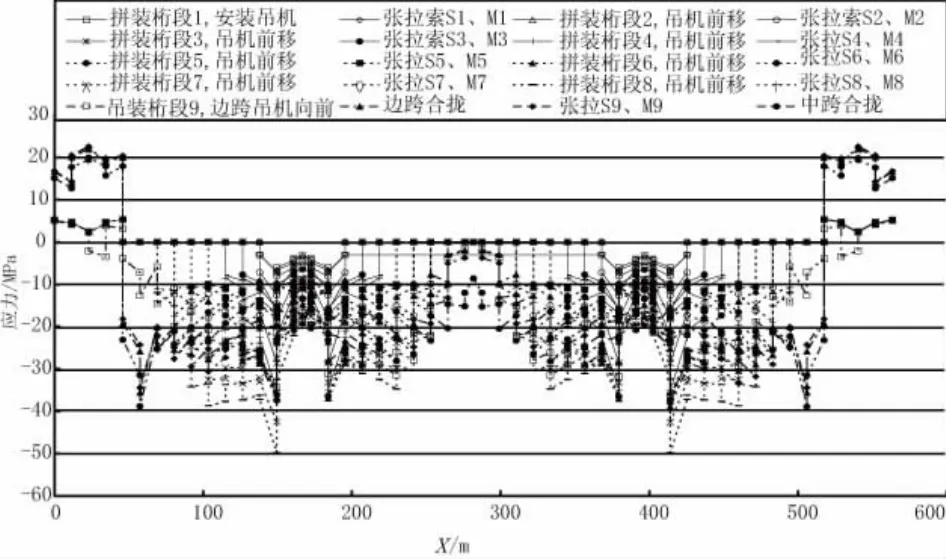
图4 悬臂施工过程中下弦杆应力图

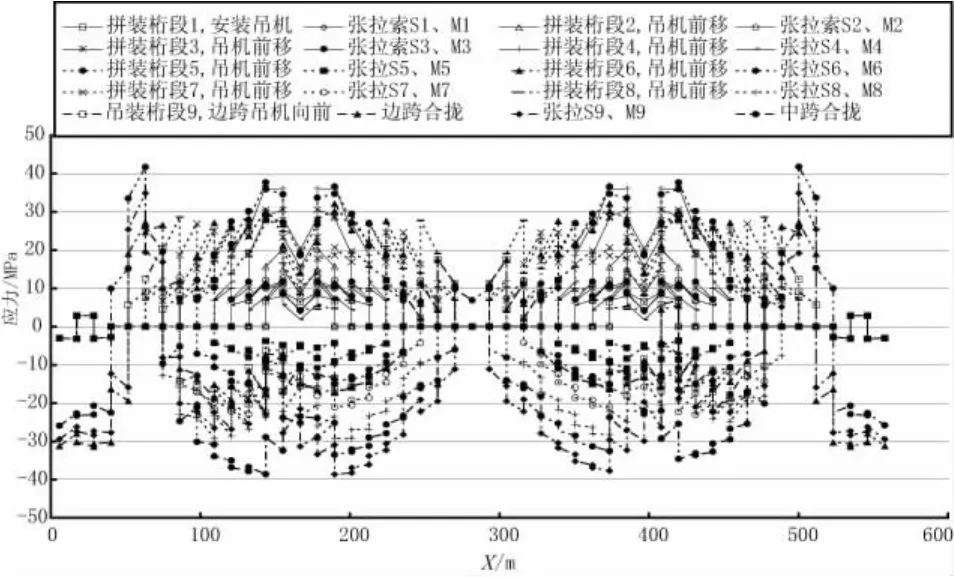
图5 悬臂施工过程中上弦杆应力图

3.3 合龙后施工阶段桥梁受力情况

合龙后施工过程中的桥梁受力情况见图6～9。由图中数据可知：桥梁受力安全。

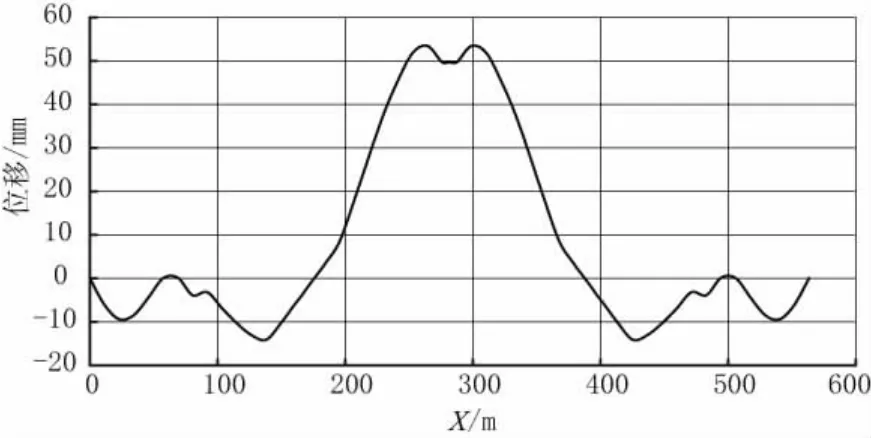
图6 成桥状态下的下弦杆竖向位移图

图7 成桥状态下的主塔顺桥向位移图

图8 成桥状态下的下弦杆应力图

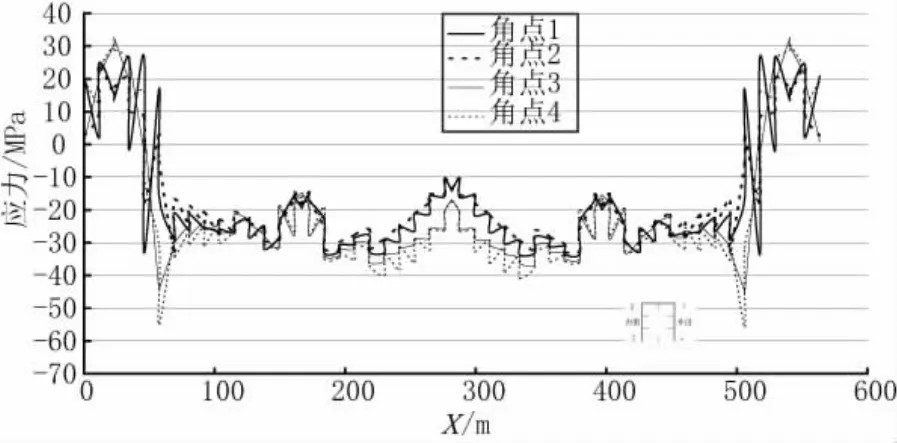
图9 成桥状态下的上弦杆应力图

4 结论

（1）采用正装迭代法对铁路钢桁梁斜拉桥的施工过程受力状态进行计算，并采用差分法对计算结果进行优化，可确定铁路钢桁梁斜拉桥的施工过程受力状态。

（2）由于铁路钢桁梁斜拉桥二期恒载占恒载比例较大，提出施工过程中各斜拉索宜张拉两次，即：悬臂施工阶段安装每根斜拉索时进行初次张拉，铺装二恒后各索再进行第二次张拉（即终张调索）。