不同采购模式下的配套部件采购策略
徐永锋
(兰州财经大学 甘肃商务发展研究中心;工商管理学院,兰州 73020)
随着全球化和信息技术的快速发展,企业之间的竞争越来越剧烈。众多跨国企业为了降低成本,往往对产品部件的采购采取集中采购模式。集中采购不仅可以通过集中企业采购资源和规模效应来降低采购成本,而且有利于维持与上游供应商的战略合作伙伴关系,从而能够在货款结算、技术开发和售后服务等诸多方面获得供应商的支持与合作,使得制造商能够在商品质量、准时交货等方面得到全面提升,增强企业的竞争力。但是集中采购这种低成本、长周期的采购模式无法满足消费者快速多变的需求,致使企业产品竞争力下降。此时,分散采购这种高成本、短周期的采购模式作为补充策略受到企业的广泛青睐。因此,当企业面临多变的市场需求时,根据以往的销售信息对市场需求进行初步预测,采用长提前期、低成本的集中采购模式提前储备一部分部件(原材料),而获得了相对比较清晰的需求更新信息后,采用短提前期、高成本的分散采购模式对不足的部分进行补充采购。这样,制造商既能够最大限度地满足快速多变的市场需求,又降低了采购成本,从而提高了制造商的利润。如何确定信息更新条件下不同采购数量成为企业采购决策的关键问题。
对于信息更新的问题,Iyer等[1]最早比较了快速反应策略与传统订货策略的差异性,为信息更新下的两次采购策略奠定了基础。随后,众多学者对该成果进行了多方面地拓展。Gurnani等[2]及Choi等[3]假设第2阶段的订货成本未知,分别在双元正态分布和贝叶斯更新的基础上,探讨了单周期两阶段两次订货策略。Lau等[4]比较了正态分布和贝塔分布的状况下,一次订货和两次订货的差异性。文献[5-8]中构建了需求信息更新下带有服务水平约束的采购策略模型,推导出零售商两个阶段的最优订货量,并分析了服务水平约束和更新信息对零售商最优订货策略及其期望利润的影响。姚泽有等[9]假设批发价格随机的情况下,探讨了不同需求和价格信息更新条件下零售商的最优订货策略和期望利润。梁罗等[10]及胡觉亮等[11]研究了需求预测更新下的零售商三阶段采购策略。李熙等[12]以均值方差理论为基础,探讨了带有风险规避特征的零售商在需求信息更新条件下的最优采购策略。宋华明等[13]构建了无信息更新、完全信息更新和部分不完全信息更新的3种采购模型,探讨了零售商在不同信息条件下的最优采购策略,并比较了不同信息类型产生的价值。王圣东等[14]建立了两生产模式和期末二次订购的Newsvendor型产品供应链协调模型,并设计了改进的收益共享契约使该供应链达到完美协调。汪峻萍等[15]将销售季末二次订购策略与销售期前的二次订购策略相结合,构建了需求信息更新点与期末紧急订购联合决策模型。Zheng等[16]构建了具有有限采购时间和最大采购数量约束的采购模型,并通过算例分析了两种供应模式对更新信息价值的影响。上述研究者对信息更新的采购策略研究仅探讨了零售商采购一种产品的最优策略。周艳菊等[17]将信息更新纳入研究框架,借助条件风险值法和基于布朗运动的贝叶斯预测方法,构建了两销售周期多产品两次订货的风险决策模型。但文献[17]中的研究是建立在产品需求独立的假设基础之上的,并且仅使用算例估计了采购策略的特征,而没有证明最优采购策略的存在性。
综上所述,虽然现有文献对信息更新下的采购策略从信息更新形式、约束条件、采购次数和风险偏好等方面进行了深入研究,但是尚存在两方面的不足:①现有文献的研究主要针对制造商和零售商构成的下游供应链中的采购问题,却很少探讨零部件供应商和制造商构成的上游供应链在需求信息更新下的采购策略;②现有研究多数建立在零售商采购单一产品或具有独立需求的多产品假设基础上,却没有考虑产品具有相关需求时的采购策略。与前人不同,本文将零部件供应商和制造商构成的上游供应链作为研究对象,假设制造商以不同的采购模式采购两种具有相关需求的部件。第1种部件仅可以使用集中模式采购,第2种部件可以按照集中采购和分散采购结合的混合方式采购。文章研究了制造商采购两配套部件的最优采购策略,并探讨了二元正态分布条件下需求更新信息质量对采购策略的影响;推导出了无有效需求更新信息以及完全需求更新信息两种情形下的最优采购策略;通过3种信息状态的比较,分析了不同信息数量和信息质量对制造商采购策略和利润的影响。
1 模型假设与符号定义
假设制造商需要采购两部件(1和2)组装其产品,两部件配套比为1∶1,组装的产品市场售价为p,市场需求为D,是一个随机变量。制造商将分别在t1和t2进行两次采购。但是由于部件1是非核心部件,制造商对部件1使用长提前期、低成本的集中采购模式进行采购,其单位采购成本为c1,采购数量为q1。部件2是核心部件,必须加强控制,制造商先根据原始需求预测使用集中采购模式采购q21的部件2。当制造商获得较为清晰的市场需求更新信息并更新需求预测后,对不足的部分以短提前期、高成本的分散采购模式作为补充,增加q22的部件2订单。具体的决策过程如图1所示。

图1 制造商采购决策过程图
显而易见,由于部件1仅能集中采购,不能分散采购补货,即不能调整采购量。因此,使用混合采购模式的部件2的累计采购量不会大于使用集中采购模式的部件1的采购量,即q2≤q1。
由图1可以看出,使用混合采购模式的部件2有两次采购机会,设两次采购的单位成本分别为c21、c22,为了避免不恰当的结果出现,假设c21<c22,(否则,企业将永远在t2进行采购)。在t1、t2期间,制造商可通过各种手段获得市场需求更新信息i,该需求更新信息是一个随机变量,其密度函数和累计分布函数分别为g(i)和G(i)。制造商通过收集需求更新信息来更新市场需求,此时市场需求的密度函数和累计分布函数分别为。企业因未满足市场需求而产生的单位缺货成本为m;过剩部件不进行组装,单位部件残值分别为l1和l2。
符号说明:
j=1,2——两种采购模式
k=s,n,p——部分需求更新信息、无有效需求信息和完全需求信息3种状态
πjk——制造商在两种采购模式时不同信息状态下的利润
V j——两个阶段的决策问题
m——制造商生产的产品单位缺货成本
l1,l2——单位部件的残值
q2j——部件2两阶段的采购数量
q1,q2——部件1、2的采购数量
q1n,q1p——部件1 无有效需求更新信息和完全需求更新信息下的采购数量
q21n,q21p——部件2无有效需求更新信息和完全需求更新信息下集中采购的采购数量
q22n,q22p——部件2无有效需求更新信息和完全需求更新信息下分散采购时的采购数量
c1——部件1的单位采购成本
D——市场需求
c2j——部件2在模式下的单位采购成本
qs1——给定需求更新信息i的条件下分位数为s1的部件2的采购量
i——市场需求更新信息
s1,sn,sp——部分有效需 求信息、无有效需求信息和完全需求信息时累计分布函数的分位数
μ2,σ2——分散采购时需求服从正态分布时的均值和均方差
μ,σ——集中采购时需求服从正态分布时的均值和均方差
ρ——集中采购时需求与其更新信息的相关系数
η,γ——需求更新信息服从正态分布时的均值和均方差
iθ(q)——市场信号阈值,θ为概率分布的分位数
对于给定的集中采购数量q1、q21和观测的市场需求更新信息i,制造商分散采购时的利润为
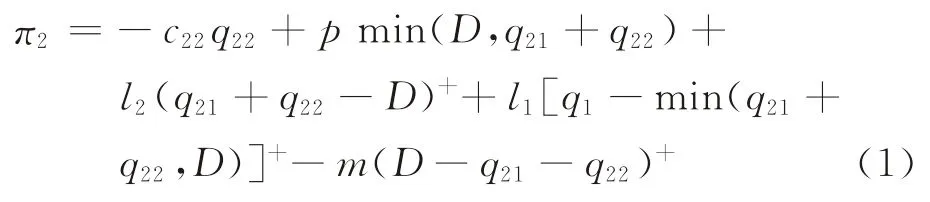
式(1)右边第1项为分散采购的采购成本,第2项及以后部分为分散采购的期望利润,即期望收入加上期望残值减去期望缺货损失。令q2=q21+q22,则式(1)第2项可写为
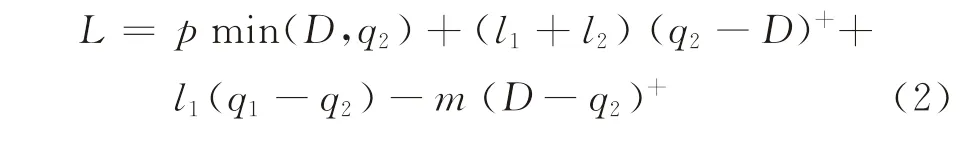
分散采购时最优采购决策即为
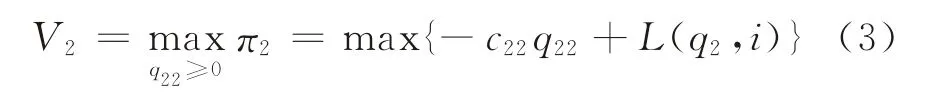
给定q1、q21和i的情况下,制造商在分散采购的问题是决定最优的分散采购时部件2的最优采购数量q22≥0,使得分散采购时的收益函数π2最大。此时,集中采购时最优问题可写为
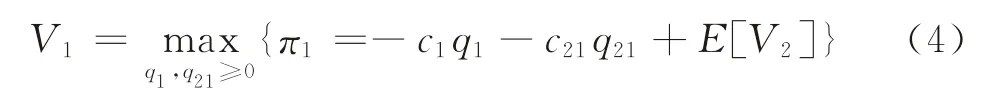
由此可见,上述问题是一个两层规划问题。为了求解方便,用部件2的累积采购数量q2替代分散采购时的采购数量q22。为了求解该二层规划问题,使用逆向求解法,即先求出分散采购的最优采购策略,将其代入集中采购最优决策问题V1中,求出集中采购的最优策略。
2 模型求解
2.1 分散采购的最优采购策略决策
由式(2)可知,
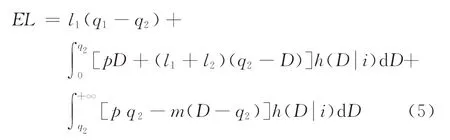
显然,对于任意给定的i,EL(q2,i)是关于q2的凹函数。在给定需求更新信息i的条件下,由制造商分散采购时的期望利润函数关于部件2的累计采购量q2的一阶条件可得
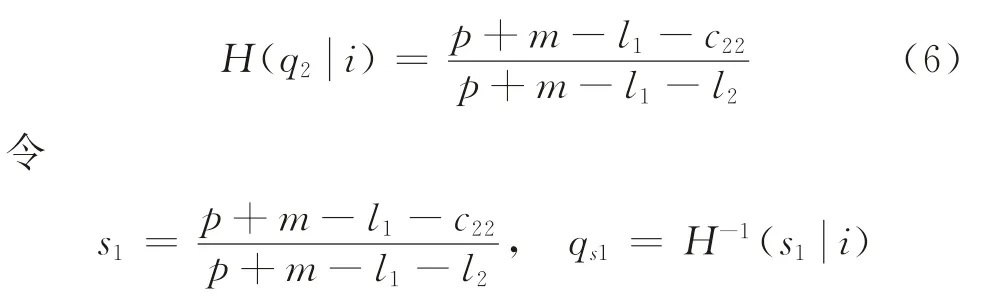
则分散采购时最优累计采购量为
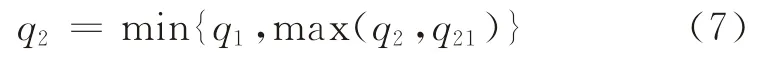
因此,分散采购时部件2的最优采购量为
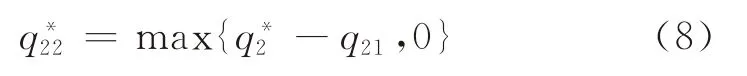
由式(7)可见,分散采购时的最优采购策略是一个分段函数。为了得到其表达式,必须对制造商获得的市场需求更新信息进行分析。
定义
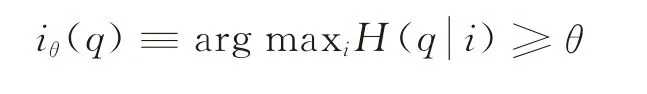
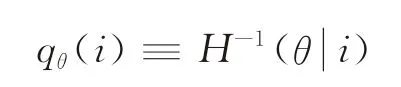
其中0<θ≤1。在给定q和θ的情况下,iθ(q)是市场信号阈值。当市场信号小于该阈值时,企业采购商品为q且满足更新需求的概率将大于θ;反之,企业采购商品为q且满足更新需求的概率将小于θ。对于任意给定的θ和i,qθ(i)是使得满足更新需求的条件概率等于θ的商品采购数量。
引理1
(1)iθ(q)是关于q的增函数,是关于θ的减函数。
(2)qθ(i)是关于θ的增函数,是关于i的增函数。
证明
(1)假设
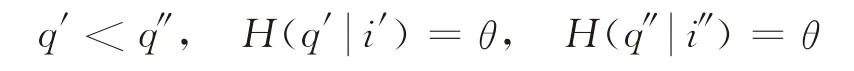
由iθ(q)的 定 义 知。由 于)是累计分布函数,故是关于q的增函数,所以有。由于,根据iθ(q)定义可得i′<i″,即iθ(q′)<iθ(q″),故是关于q的增函数。假设0<θ′<θ″≤1,
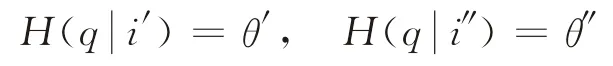
(2)根据qθ(i)的定义及是关于q的增函数,可知其反函数为θ的增函数。假设i′<i″。根据qθ(i)的定义及反函数的性质可得
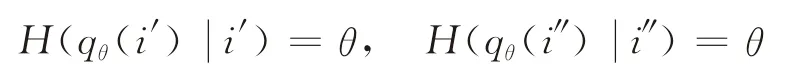
由于i′<i″,故有
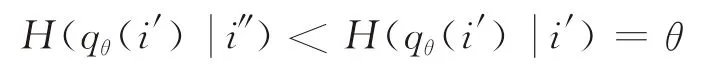
定理1对于任意给定的集中采购组合(q1,q21)和制造商获得市场信号i,最优的分散采购数量满足:
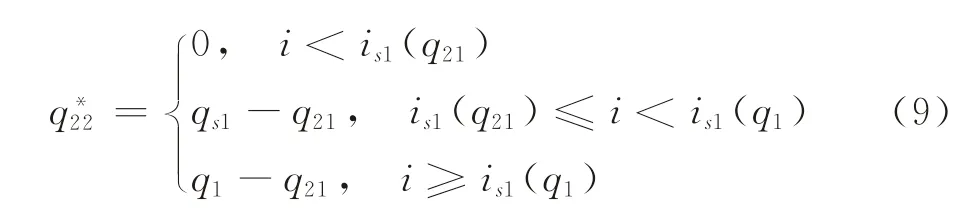
证明根据引理1(1)和假设条件q1≥q21,可得is1(q21)≤is1(q1)。如果i<is1(q21),根据引理1(2)可知,
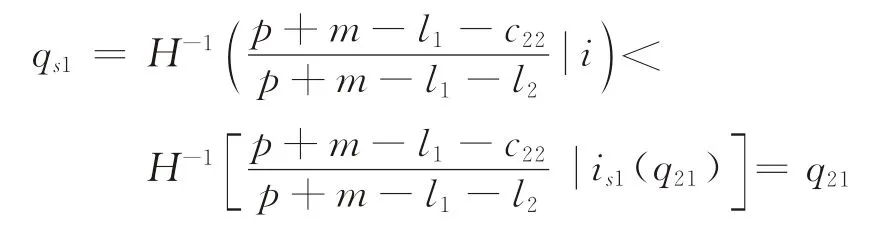
由式(7)可知,
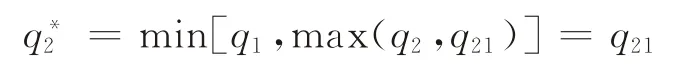
因此,由式(8)可知,
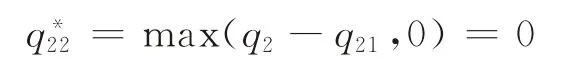
同理,如 果is1(q21)≤i<is1(q1),可 知q21≤qs1<q1,因此,
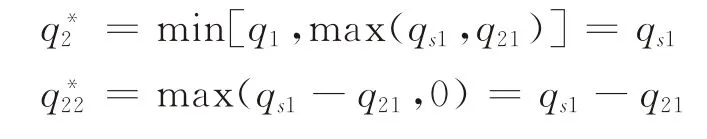
同理,如果i≥is1(q1),因此,
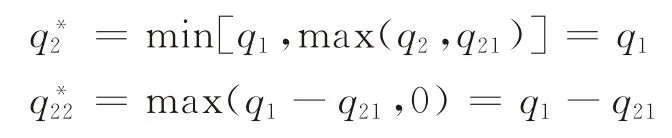
由于部件1、2是配套性产品,其必须配套使用,故当制造商集中采购时,部件2的采购量不应当大于部件1的采购量,否则部件2将产生剩余,会造成浪费。当制造商集中采购时,部件2的采购量小于部件1的采购量,其可以通过分散采购补充部件2的数量。如果制造商获得需求更新信息后发现市场需求小于集中采购时部件2 的采购数量,即i<is1(q21),制造商同样不会进行分散采购;反之,当制造商获得需求更新信息后发现市场需求大于集中采购时部件2的采购数量,但小于部件1的采购数量,即is1(q21)≤i<is1(q1),此时制造商累计采购部件2的数量正好满足市场需求,即qs1-q21;而当制造商获得需求更新信息后发现市场需求大于部件1的采购数量,即i≥is1(q1)时,此时两部件采购数量正好配套,制造商分散采购部件2的数量正好是集中采购时两部件的差额。
2.2 集中采购的最优采购策略决策
要求得制造商集中采购最优采购策略,必须证明最优策略的存在性。因此,将制造商分散采购时的最优解代入集中采购的期望利润函数中,证明二阶导数小于0即可。但是由于制造商分散采购时最优采购策略是分段函数,故在集中采购时应当分段分析。
定理2制造商集中采购时的期望利润E(π1)是关于集中采购时的采购数量q1、q21的联合凹函数。
证明由于q1≥q21,根据引理1和定理1,可将式(4)重写为
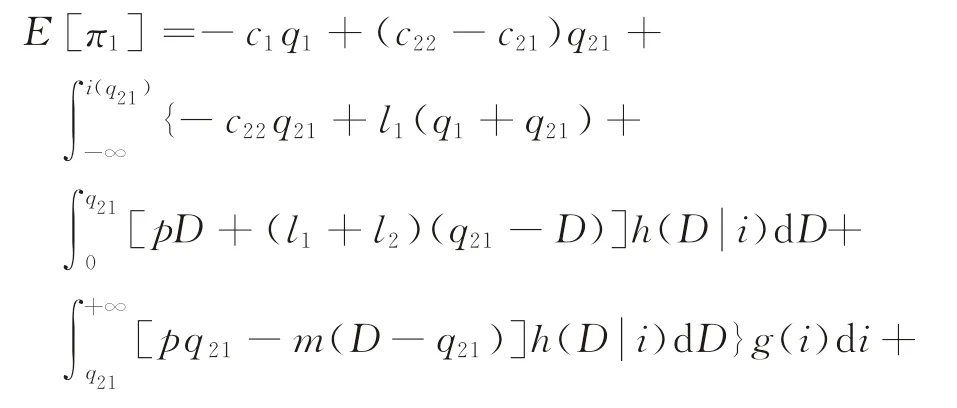
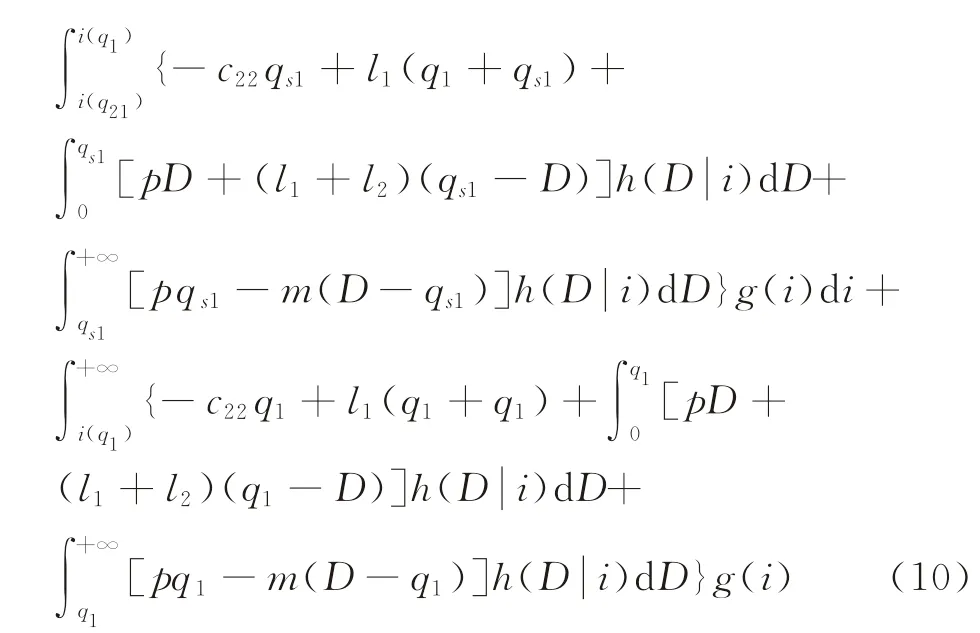
制造商的期望利润函数关于q1、q21的二阶偏导数和混合偏导数分别为:
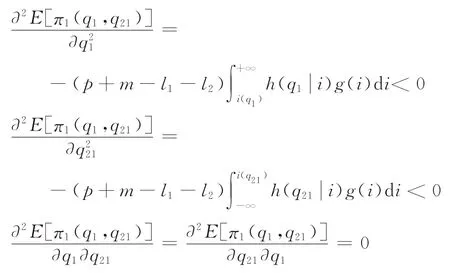
因此,可得其海塞矩阵K的行列式为
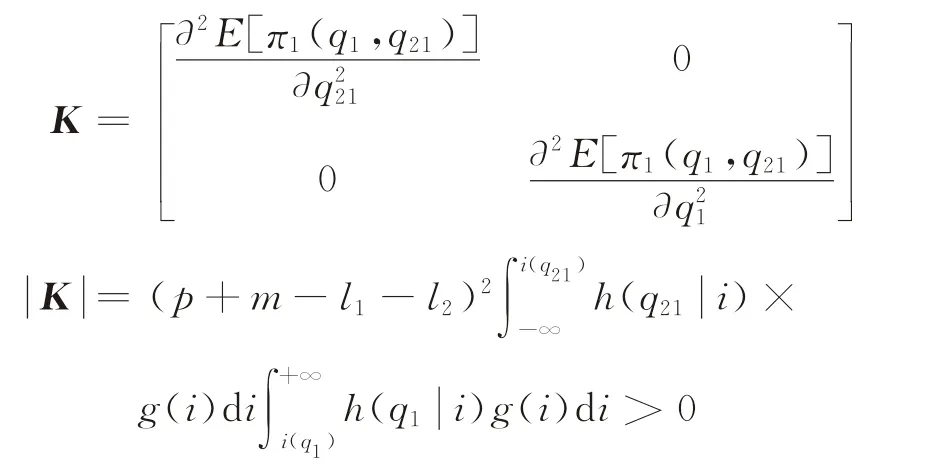
由于海塞矩阵K一阶顺序主子式小于0、二阶顺序主子式大于0,故该曲面凹向原点,即制造商集中采购时的期望利润E[π1]是关于集中采购时的采购数量q1、q21的联合凹函数。
定理2说明,总是存在一组最优的采购策略,使得其利润最大。制造商集中采购时的决策目标就是找到这一组最优的采购策略。
定理3制造商集中采购时的最优采购策略由下式决定:
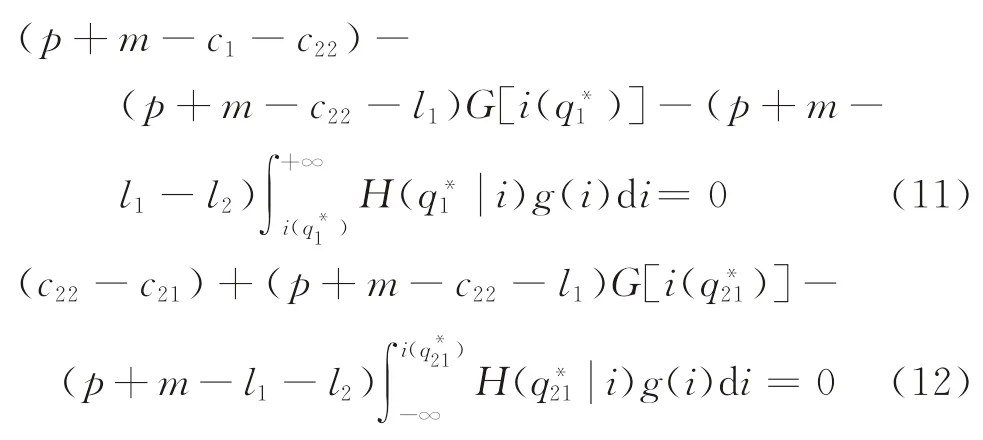
证明由式(10)关于q1、q21的一阶导数为0即可得到。
特别地,当q1=q21时,制造商集中采购时的最优采购策略为
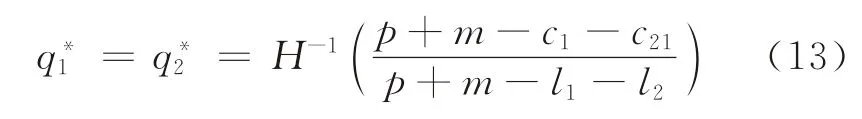
上述讨论都是假设制造商获得的需求更新信息仅能部分揭示市场需求的情况,下面将分析两种极端情况:①制造商在分散采购时无法获得任何关于市场需求的有效信息;②制造商在分散采购时可以获得全部市场需求信息。
2.3 无有效信息和完全信息时的采购策略分析
2.3.1 需求更新信息无效时的采购策略 无效需求更新信息是指制造商在两次采购期间搜集的市场需求更新信息对需求不确定性无任何影响。用数学语言刻画即为需求更新信息i和市场需求D相互独立,因此,有。由于制造企业在t2时获得的需求更新信息对更新市场需求没有帮助,并且,部件2在t2时的采购成本比t1时高;同时,部件1与部件2是配套商品,必须配套使用才有价值,故企业的最优采购策略必然与集中采购时采购相同数量的部件1 与部件2,分散采购时不进行采购。该问题实际上退化为无需求信息更新的单阶段报童模型。此时,两部件集中采购数量相同,即
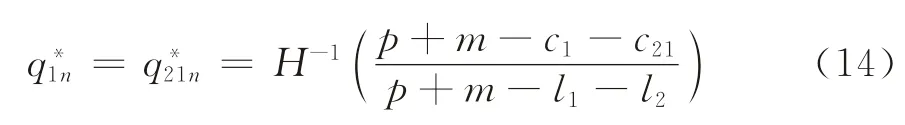
2.3.2 完全需求更新信息情况的采购策略 在这部分研究另一个极端情况,即制造企业获得关于市场需求的全部信息。在完全需求更新信息情况下,市场需求D成为市场需求更新信息i的函数,可表示为D=τ(i)。由采购的性质可知,D=τ(i)是关于市场需求更新信息i的增函数。为方便起见,假设D=τ(i)的反函数存在,则制造企业的期望利润为
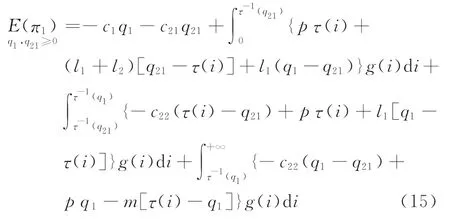
按照定理2相同的证明方法,可得制造商期望利润函数的海塞矩阵为:
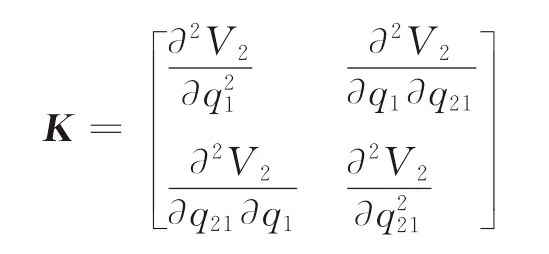
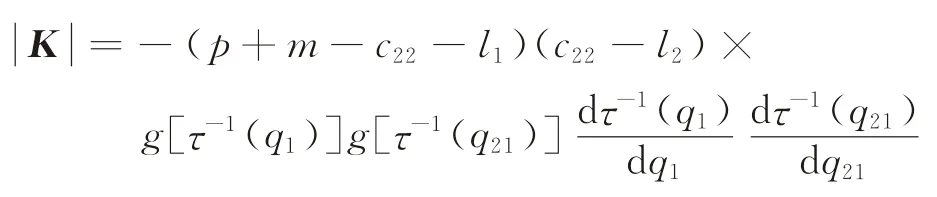
因为D=τ(i)是关于i的增函数,所以其反函数是关于D的增函数,因此,有dτ-1(D)/dD>0。其一阶顺序主子式小于0,而二阶顺序主子式大于0,因此,该函数是凹的。
根据式(15)关于q1、q21的一阶条件可知,制造企业集中采购时最优的采购策略为:
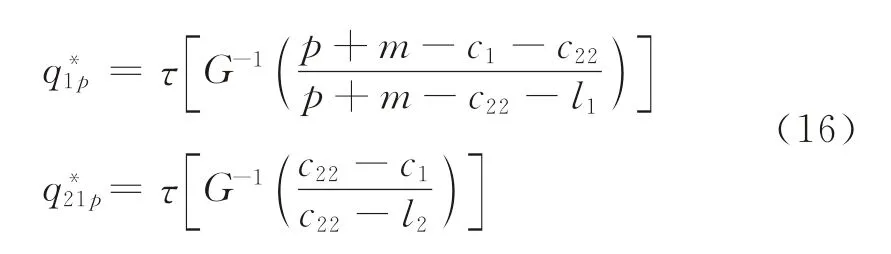
由前文的分析可见,制造商的采购策略与其在分散采购时能够获取的需求更新信息有很大的相关性,因此,有必要对制造商获取的需求更新信息质量和最优采购策略的相互关系进行分析。由于部分需求更新信息下制造商的采购策略由式(11)、(12)所决定,可以看出,采购策略是一个隐函数,为了分析需求更新信息质量对最优采购策略的影响,本文选择二元正态分布这一特殊的分布来进行讨论。
2.4 需求更新信息质量对最优采购策略的影响
假设市场需求更新信息i和需求D服从均值为η和μ、标准差为γ和σ、相关系数为ρ的二元正态分布,因此,可得市场需求更新信息i的边际分布密度函数g(.)服从均值为η、标准差为γ的正态分布。更新后的市场需求密度函数为条件密度函数,其服从均值μ2=μ+ρσ(i-η)/γ、均方差的正态分布。因此,可知:
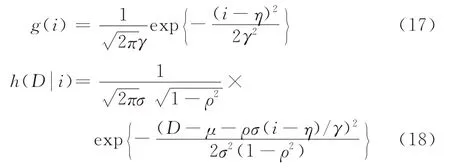
明显地,其累计分布函数G(i)和是关于D和i的严格增函数。由引理1分析可知:
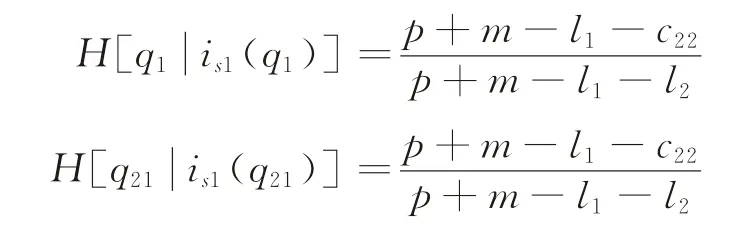
因此,可得:
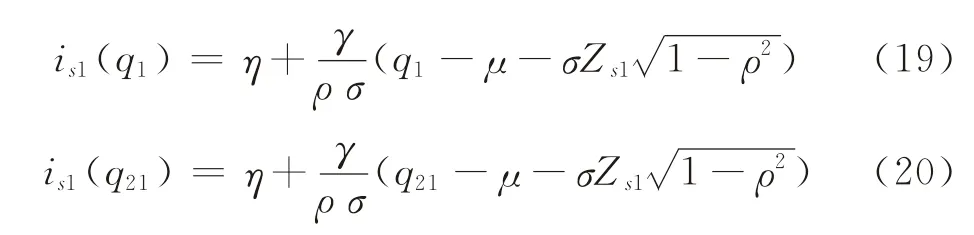
式中,Zs1为分位数为s1时标准正态值。同样可得q1和q21关于需求更新信息i的表达式分别为:
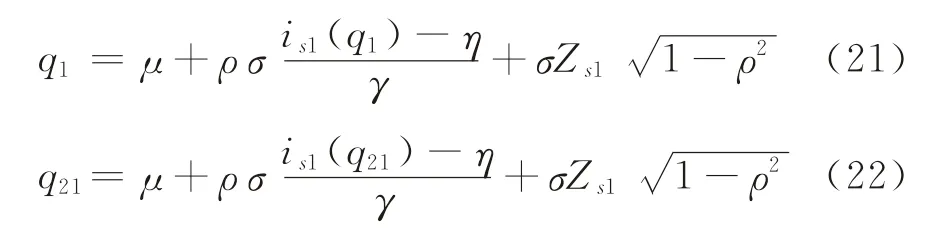
定理4当时,随着制造企业获取需求更新信息的质量ρ提高,其在集中采购时采购部件1的数量将增加,而采购部件2的数量将减少;当时,需求更新信息质量ρ的高低与第1阶段采购策略无关。
证明当时,首先讨论与ρ的关系。根据式(11),假设
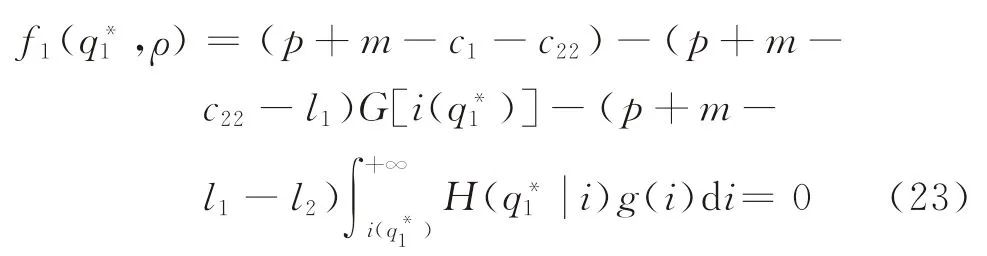
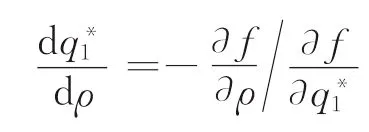
分别确定该等式分子分母的符号。根据式(23)可得
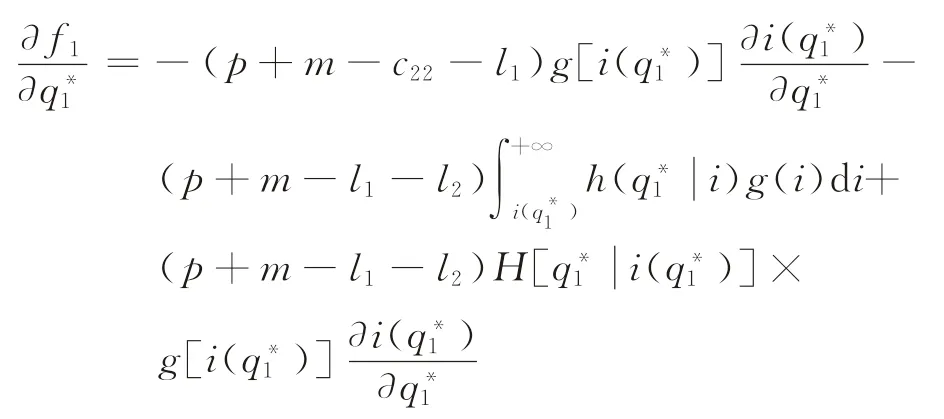
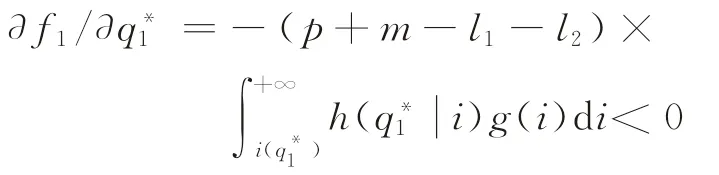
结合∂f/∂ρ<0和可知,。
其次,讨论q21与ρ的关系。根据式(12),假设
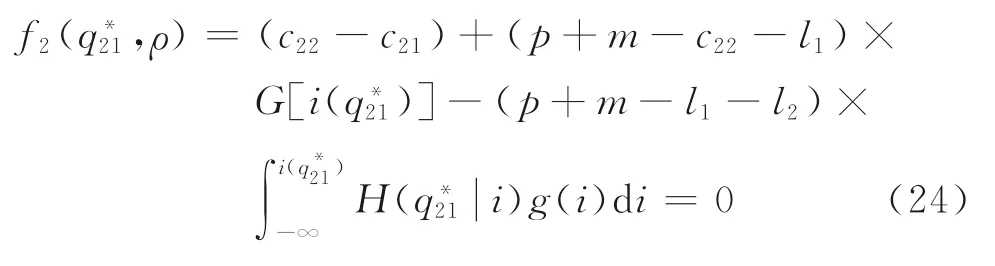
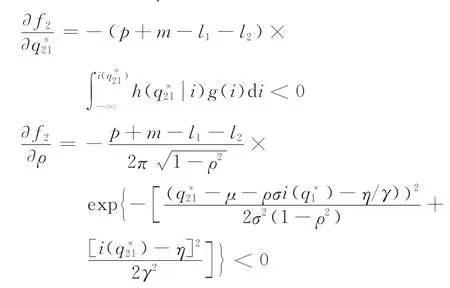
结合∂f/∂ρ<0和可知,。
定理4表示,当参数一定的条件下,随着需求更新信息质量的提高,制造企业对部件1的采购量将增加。这是因为由于制造企业只能在集中采购时采购部件1,其预见到其在分散采购时能够获得更准确的需求更新信息,为了把握市场机会,避免因部件不配套而带来的缺货损失,企业将更加冒险,从而采购更多的部件1。而随着需求更新信息质量的提高,制造企业集中采购时对部件2的采购量将减少。这是因为企业有机会在分散采购时依据更为准确的需求更新信息进行补充采购,从而避免了提前采购数量过多造成的浪费。这一结论与Gurnani等[2]的命题3.4中的结论相符。定理4还说明,在特定条件下,即使制造企业有能力获得更准确的市场需求信息,但是由于部件采购成本和配套性的约束,导致企业并不是总能利用这种需求更新信息优势。
3 算例验证
(1)信息数量的敏感性分析。假设制造商面临的市场需求与更新信息服从N(35,10,20,6,0.5)的二元正态分布。产品销售价格p=3,产品缺货损失m=1,部件1的集中采购成本c1=1,残值l1=0.5,部件2的集中采购成本和分散采购成本分别为:c21=1,c22=1.5,残值l2=0.5。可得部件2的累计采购数量如图2所示。由图2可见,当更新信息i≤12.9或大于i≥16.9时,部件2的累计采购数量均为直线,分别为:
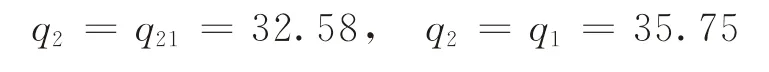
这是因为当制造商获得较少的信息时,由于不确定性下降节约的成本不足以补偿分散采购增加的成本,此时企业不会采取分散采购;当信息获得较多时,虽然不确定性下降节约的成本大于分散采购增加的成本,但是由于部件配套性的限制,制造商分散采购数量最多是两部件集中采购的差额。当更新信息介于12.9<i<16.9时,部件2分散采购数量不断增大,这与定理1相符。
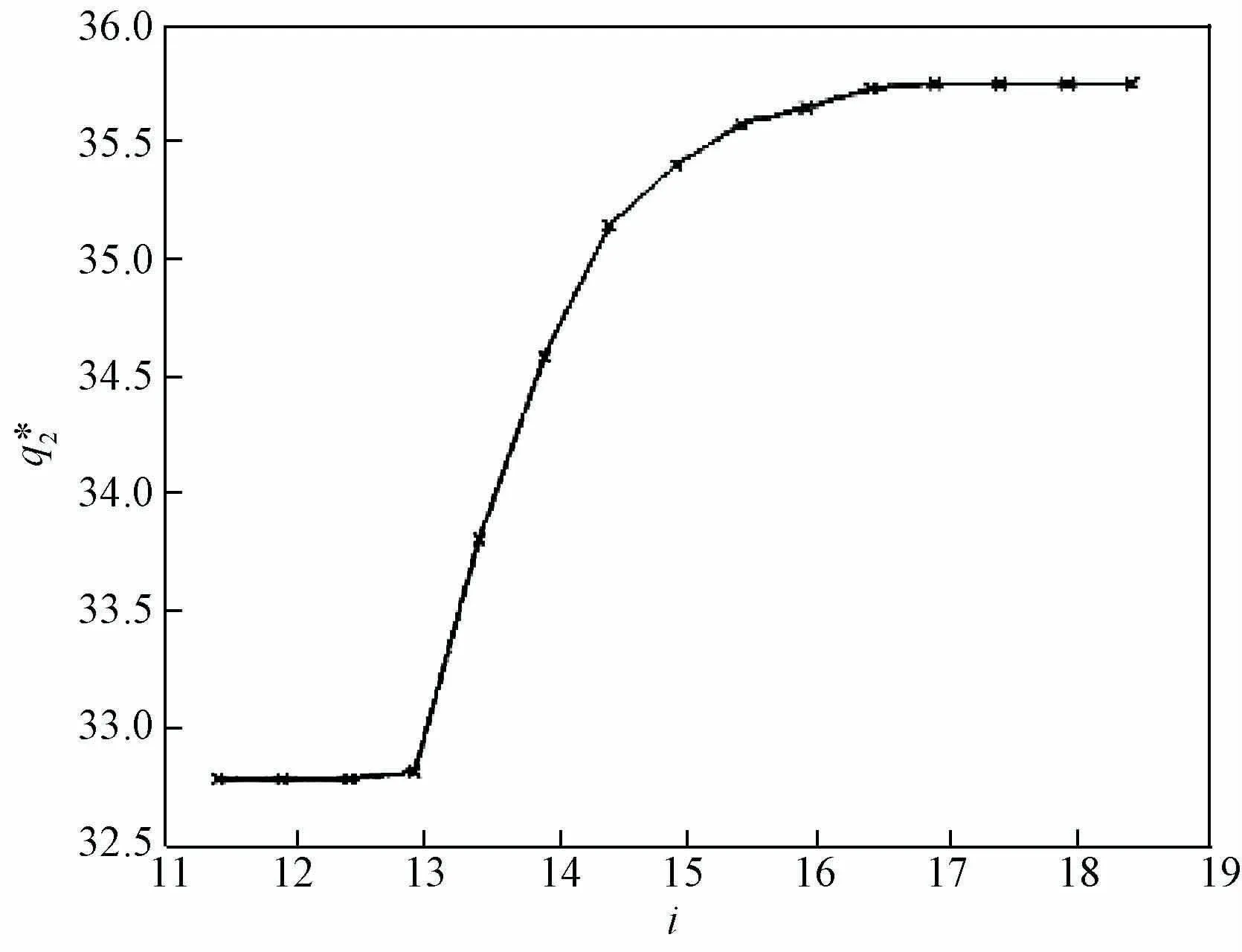
图2 部件2累计采购数量变动趋势
(2)信息质量的敏感性分析。首先考察信息质量对集中采购策略的影响。假设其他参数值不变,市场需求与更新信息的相关度不断增大,可以得到集中采购数量变动趋势,如图3所示。
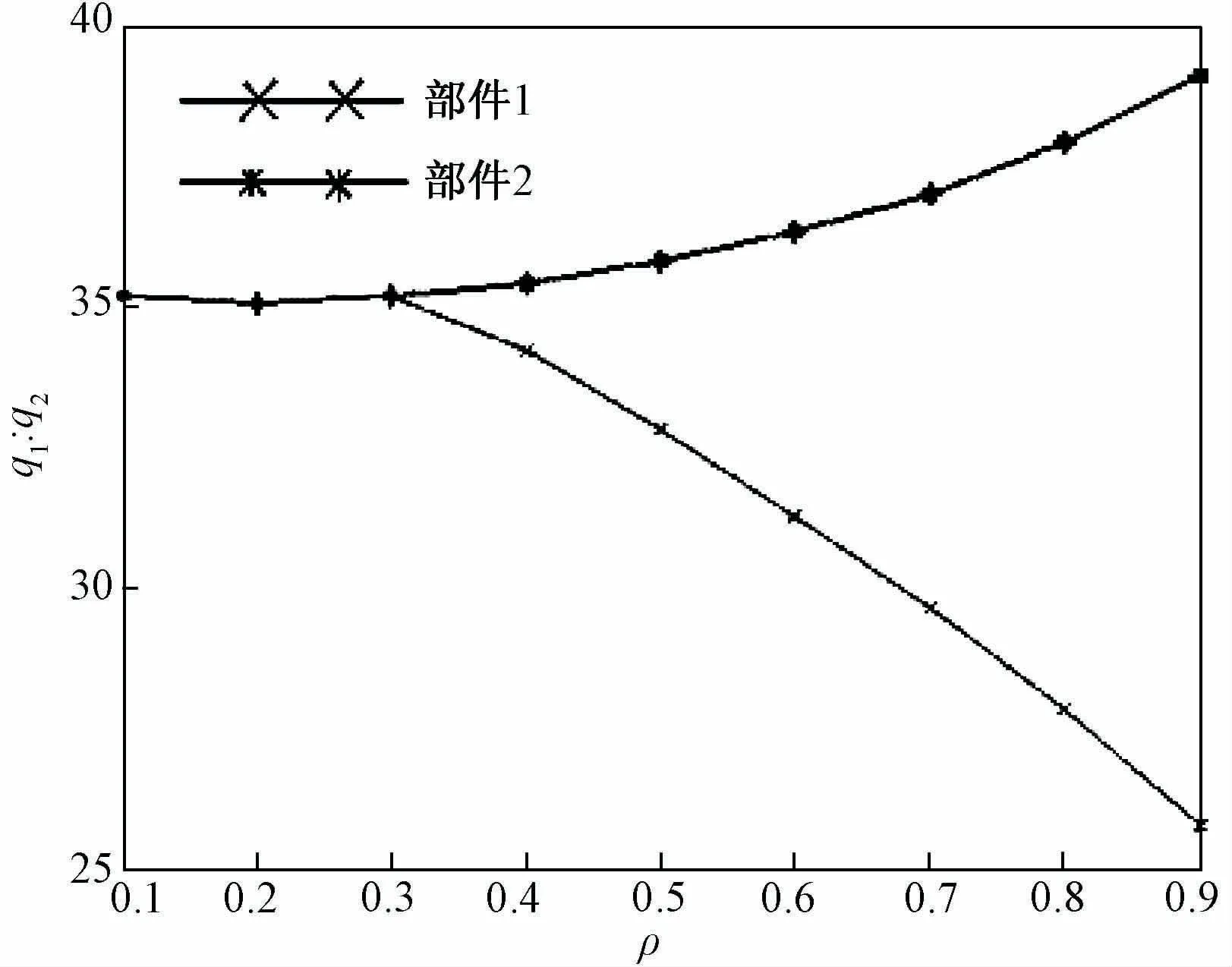
图3 集中采购数量变动趋势
由图3可见,当更新信息的相关度大于0.3时,随着市场需求与更新信息的相关度不断增大,部件1的集中采购数量不断增大,而部件2的集中采购数量不断减小。这是因为市场需求与更新信息的相关度越大,制造商在分散采购阶段对市场需求的预测越准确,由于部件2允许分散采购,为了减少不确定性带来的过剩或短缺损失,制造商更倾向于使用分散采购模式采购部件2,从而减少了集中采购部件2的数量。而由于制造商在集中采购阶段知道分散采购阶段能够非常准确地的预测市场信息,为了减少因部件不配套带来的缺货损失,制造商对部件1的采购将会采用更加冒险的策略,即将增加部件1的集中采购数量。
但是制造商并非总能利用高质量的更新信息。当产品销售价格p=3.2,i产品的缺货损失m=0.5,部件2分散采购成本分别为c22=2时,其他参数不变,即使市场需求与更新信息相关性达到0.7,也即信息质量很高的情况下,制造商也不会采用分散采购模式。此时,制造商仅会使用集中采购模式,采购量为:。这是由于部件配套性使得利用高质量信息增加的成本高于需求不确定性降低节约的成本,此时制造商利用高质量信息不会得到更高的收益,反而会统一采用集中采购模式。
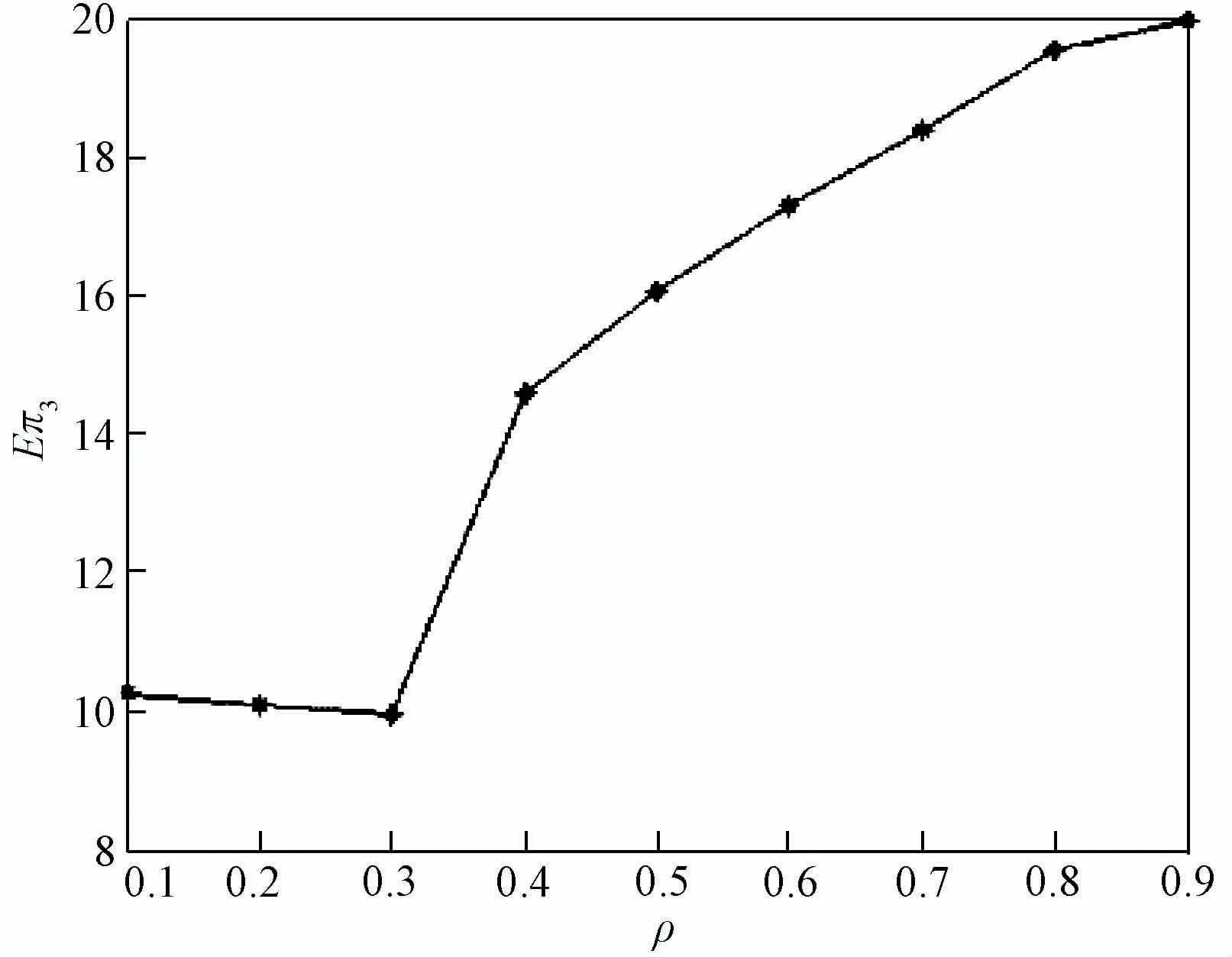
图4 制造商利润变动趋势
其次,进一步考察信息质量对制造商利润的影响。除市场需求与更新信息的相关系数外,还有其他参数与信息数量的敏感性分析中的假设一致。由图4可以看出,当市场需求与更新信息的相关度大于0.3时,随着市场需求与更新信息的相关度的增大,制造商采购数量不断增大,并且曲线凹向原点。这是因为制造商获得了较为准确的市场需求信息,使得制造商部件2的采购更为准确,从而降低了该部件的缺货损失或过剩成本,带来制造商期望利润增加;当相关度不断增大时,需求不确定的范围不断减小,故对制造商期望利润的影响幅度在减小,所以表现为边际利润减小,这符合边际报酬递减规律。当市场需求与更新信息的相关度小于0.3时,制造商的利润近似于一条水平线。这是由于此时两部件面临相同的需求不确定性,其采购数量相同,市场需求与更新信息的相关度对利润的影响太小,可以忽略不计。
4 结 语
传统信息更新下的采购决策模型均未考虑采购商的采购模式与部件的相关性。本文将两者纳入到信息更新条件下的采购决策模型中。通过采购商的利润最大化,证明了其最优采购策略的存在性及其存在形式,并进一步探讨了更新信息质量对集中采购策略的影响。发现随着需求更新信息质量的提高,制造企业对仅采用集中采购模式的部件的采购量将增加,而采用混合采购模式的部件集中采购数量将减少,也即更倾向于使用分散采购。但是由于部件采购成本和配套性的约束导致企业并不是总能利用这种需求更新信息优势。
本文没有考虑信息更新时机、库存成本和供应链利润最大化等问题。因此,在今后研究中可从两个方面来深入探讨:①当信息更新时机不同,考虑库存成本时,采购策略会否发生变化;②当考虑供应链利润最大化的条件下,采购策略是否会发生变化。

