融合HOG类特征的尺度自适应压缩跟踪算法

景星烁， 邹卫军， 夏 婷， 李 超， 许 旭

(1.南京理工大学，南京 210094； 2.山东农业大学，山东 泰安 271018)

0 引言

目标跟踪是在连续的图像序列中估计目标的位置，需要面临诸多困难，是一个具有挑战性的难题。最初的研究算法主要是基于生成模型来进行跟踪，如文献[1-2]，但这些算法的鲁棒性不是太高，计算量很大，不适合进行实时跟踪。随着目标跟踪算法的进一步发展，基于判别模型[3]的跟踪成为研究热点。基于压缩感知理论[4]的压缩跟踪算法[5]就是基于判别模型，通过生成一个稀疏的投影矩阵，然后将压缩后的数据作为特征来进行分类，优点是简单、高效；但该算法仍存在一些缺陷，如对光照比较敏感，而且不能适应目标尺度的变化。随后，研究人员在压缩跟踪的基础上也做了一些改进。文献[6]以多个矩阵作为压缩感知中的投影矩阵，将压缩后的数据作为特征提取出跟踪所需的多种特征，使算法能够适应纹理和光照变化，但跟踪框大小固定，所以不能够适应目标尺度的变化。文献[7]通过结构约束性采样，获取不同位置不同尺度的扫描窗，离线计算不同尺度下的稀疏随机感知矩阵，并用于降维，解决了目标的基本姿态变化及尺度缩放的问题，但是没有解决光照变化、遮挡等问题。

本文综合考虑以上缺陷，提出了改进算法：分析了HOG类特征对光照的不敏感性，与Haar-like特征采用固定比值方式进行融合，并结合尺度估计相关滤波器[8]，寻找使滤波器得到最大响应的尺度，更新特征提取模板，从而实时地调整跟踪窗口进行精确跟踪。

1 CT算法相关概念

压缩跟踪算法的主要思想就是利用符合压缩感知RIP条件的随机感知矩阵对高维图像特征进行降维，并且对降维后的特征采用简单的朴素贝叶斯分类器进行二分类，然后每帧通过在线学习更新分类器，实现目标跟踪。基于压缩感知理论[4]的降维公式可以描述为：V=RX，其中,X为高维特征信号(m维)，V为低维特征信号(n维)，R代表随机测量矩阵。其特征降维过程为

(1)

2 Haar-like特征与HOG类特征的融合

2.1 Haar-like特征算法

Haar-like特征[5]是通过统计多个矩形框内的像素和，然后由这几个矩形框内的像素和线性表示而成，此特征在图像内的不同区域形成像素灰度特征，在目标发生一定形变时有较好的鲁棒性，但是该特征由于引入的是颜色信息，所以对光照比较敏感，不能应对较大的光照变化情况。

每个样本[5]的Haar-like特征算式为

(2)

式中：f(i)为第i个特征；Rrect(rk)为第k个矩形框内像素值的和；wk为第k个矩形框的权重；N是矩形特征f(i)中含有的矩形框总个数，其值在2～4之间。

2.2 HOG类特征算法

2005年，DALAL提出HOG(梯度向量直方图)[9]特征，是指使用梯度的幅值和方向围绕兴趣点或图像的一个区域构建直方图。HOG特征表征了图像矩形区域内的梯度强度和梯度方向的分布情况，由于它是在图像的局部单元上操作的，所以对图像的几何和光学上的形变有着良好的不变性，弥补了Haar-like特征的不足。

计算HOG特征时首先要计算像素的梯度与梯度方向。图像各像素点(x,y)的梯度算式为

Gx(x,y)=i(x+1,y)-i(x-1,y)

(3)

Gy(x,y)=i(x,y+1)-i(x,y-1)

(4)

式中，Gx(x,y)，Gy(x,y)，i(x,y)分别代表输入图像中像素点A(x,y)水平方向上的梯度、垂直方向上的梯度和该点像素值。所以，该像素点的梯度值与梯度方向分别为

(5)

θ=arctan(Gx/Gy)。

(6)

但是，使用上式直接计算梯度，计算量十分巨大，不能满足实时性的要求，所以实际计算时采用中心向量算子[9][1，0，-1]来估计梯度。

为了与Haar-like特征进行融合，本文提出一种有别于传统HOG特征的HOG类特征表示方法：在采集得到正负样本之后，首先计算每个样本图像中所有像素点的梯度和梯度方向。其次，把梯度方向平均分成B个特征区间，按照每个像素点的梯度方向统计各像素点的梯度向量直方图。最终，在每个特征区间，都能得到一幅梯度幅值图像，进而得到B幅梯度幅值图像。根据式(2)，对每个梯度幅值图像分别采用与Haar-like相同的处理方法，便可以得到上文所提到的HOG类特征。其特征数量为Haar-like特征数量的B倍。

由于每个Haar-like特征与HOG类特征提取时要统计矩形框内像素的和，计算量是十分庞大的，无法满足实际要求。为了减少计算量，本文仍采用积分图像[5]进行加速运算。

2.3 特征融合

在实际提取特征时，需要使用上述所提到的随机测量矩阵的方法进行降维。本文采用Haar-like特征与HOG类特征固定比值融合的方法，提取图像更多有用的信息。利用随机测量矩阵将高维特征X投影到低维空间。

vi=(yi1,yi 2,…,yiB,zi)

(7)

V=(v1,v2,…，vn)=RX

(8)

式中：(yi1,yi 2,…,yiB)代表HOG类特征值，B代表每个融合特征组中HOG类特征个数；zi代表Haar-like特征值；V代表压缩之后的特征向量，即通过随机测量矩阵R得到的所有融合特征组。本文为了保持算法的实时性，在特征融合过程中采用的是固定比值融合，即参与训练的Haar-like特征数与HOG类特征数的比值设置为1:B(B的大小可以根据不同场景和目标特征进行适当调整)，然后使用融合特征组训练和更新分类器并进行分类。

2.4 朴素贝叶斯分类器的构建与更新

对于上述所计算的Haar-like与HOG类特征组，本文仍采用朴素贝叶斯分类器进行分类，假定V中的各元素是独立分布的，构建分类器为

(9)

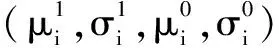
(10)

这4个参数会进行增量更新，即

(11)

式中：学习因子λ>0；

(12)

式(11)可以由最大化似然估计[5]得到。

3 自适应尺度相关滤波器的设计

3.1 滤波器的设计

针对目标运动过程中出现的尺度变化问题，本文借鉴多尺度跟踪方法[10]，通过学习一个独立的一维相关滤波器去检测目标尺度的变化，称之为尺度相关滤波器。尺度估计方法为：首先在检测出的目标周围采集一系列不同尺度的图像块xsi，提取d维HOG特征进行图像块表达，对应的高斯函数标签为ysi；利用这些图像块训练RLS分类器[9]，并在线性空间进行求解，获得一个一维的尺度相关滤波器；最后通过寻找这个滤波器的最大输出响应来完成尺度检测。

训练RLS分类器，得到尺度相关滤波器模板Bnum，Bden的计算和更新公式分别为

Bnum(i)=(1-ηs)Bnum(i-1)+ηsF(ysi)⊙F*(xsi)

(13)

(14)

式中，ηs是固定的参数。

尺度分类器的输出响应为

(15)

随着目标尺度的变化，特征提取模板也要变化。本文采用比例缩放的方式更新模板，即通过缩放特征模板中小矩形框的大小来保证适应目标尺度的改变。

3.2 改进后的整体算法流程

改进后的算法流程如下：

1) 初始化有关参数[5,10]并手动设定第一帧中被跟踪目标的中心位置及尺度；

2) 读取新帧图像，判断是否为初始帧，若是，转到8);否则,转3)；

3) 在图像上一帧的目标中心位置的候选区域(距离半径r≤γ[5])中提取候选样本，并计算Haar-like和HOG类特征组的特征值；

4) 使用朴素贝叶斯分类器从候选区域中找到使分类数最大的目标中心位置作为新位置；

5) 在新目标区域周围为尺度相关滤波器提取33个尺度样本[10]，并计算其特征值；

6) 计算尺度分类器的响应值，找到最大响应时的尺度；

7) 更新目标尺度，并更新特征模板；

8) 在图像目标中心的内邻域(距离半径r≤α[5])与环形域(距离半径ζ≤r≤β[5])分别提取当前尺度的正样本和负样本，用稀疏测量矩阵在正负样本上提取Haar-like和HOG类特征组，并计算特征值；

9) 由8)得到的特征值更新朴素贝叶斯分类器参数；

10) 在目标区域周围为尺度相关滤波器提取33个尺度样本[10]，并计算样本特征值；

11) 更新尺度分类器的参数；

12) 判断是否为最后一帧，如果是，则算法终止；否则,转到2)。

4 实验结果及分析

本文实验的计算机配置为：处理器为Intel(R) Core(TIM) i5-3230M CPU@2.60 GHz，内存为8.00 GB，64位Windows8 操作系统。开发环境为Matlab与C++的混合编译环境，版本为Matlab 2014a。实验中所用到的6组视频序列来自公开的OTB数据集，每个视频序列的特点如表1所示。Struck跟踪算法[11]是基于结构输出预测的自适应目标跟踪框架，利用支持向量机(SVM) 原理实现跟踪，其跟踪速度与精度都不错。实验中，对比了原始压缩跟踪算法和Struck跟踪算法，并在下文做出了具体分析。

表1 各视频序列的特点

4.1 参数设置及评价指标

实验过程中，设置基本参数为：梯度区间B取4，Haar-like特征数仍然取原始压缩跟踪算法中的50，学习率为0.85，α=4，β=30，ζ=8，γ=20；有关尺度估计的参数设置见文献[10]。

中心距离精度PD、重叠率RO、中心位置误差ECL是度量跟踪算法性能的重要指标。其中：ECL是跟踪目标位置与实际位置的欧氏距离，单位为像素；PD是ECL<20的帧数占总帧数的比值；RO的定义为

(16)

式中：RT为跟踪得到的目标框；RG为标定目标框；S(·)表示矩形框(·)的面积。当RO大于0.5时，认为可以成功跟踪到目标。

4.2 定性结果比较

选取的6组视频序列分别用Struck算法、CT算法及本文算法进行跟踪测试，跟踪效果对比如图1所示。

通过以上跟踪结果的定性对比，并且结合每个视频序列所具有的特点，可以分以下几种情况进行分析。

光照变化情况：图1c、图1d、图1e中所示的视频序列展示了光照变化对跟踪算法的影响。对于CarDark序列，在夜晚道路上有明显的光照变化，原始CT算法在开始时就已经跟踪失败，而Struck算法开始时跟踪良好，但后期目标框产生了少许偏移，本文算法整体跟踪都十分成功；Man序列中黑暗背景下CT算法与本文算法跟踪很好，但发生光照剧烈变化时，CT算法跟踪失败，本文算法仍然可以精确跟踪；Trellis序列中的光照变化也十分明显，可以看到后期光照变化时Struck算法与CT算法直接跟丢目标，而本文算法十分稳定。可以看出，Struck算法与CT算法对光照都十分敏感。

尺度变化情况：图1a、图1b、图1e、图1f所示序列都有目标的尺度变化，明显看出,本文算法在加入了尺度自适应算法后效果比未加入尺度估计的Struck算法和CT算法效果更好。

旋转与形变问题：图1a、图1b所示序列都涉及平面内旋转问题，由Dog1序列中第650帧可以看出，本文算法应对此类问题比其他两类算法更好，Dog2序列中的形变问题在第70，96，113帧可以明显对比，Struck算法与CT算法跟踪的目标位置已经出现了偏移，效果不如本文算法。图1e中涉及平面外旋转，可以看出,本文算法在应对平面外旋转的情况时鲁棒性有所欠缺。

背景相似干扰与部分遮挡问题：图1c、图1e所示序列中含有背景相似干扰，CarDark序列中Struck算法与本文算法都可以成功跟踪，而在Trellis序列中只有本文算法可以成功跟踪。对于Walking中的部分遮挡问题，本文算法与Struck算法都能跟踪目标，且效果较Struck算法好一些。

综合以上分析，本文算法不仅能够大大降低对光照的敏感度，而且还能适应目标尺度的变化，另外，对于一些平面内旋转形变及部分遮挡问题也能进行跟踪，算法鲁棒性有了一定的提高。

4.3 定量分析结果

分别针对Struck算法、CT算法及本文算法的目标跟踪结果定量计算出中心距离精度、重叠率以及中心位置误差3项评价指标，如表2所示，并绘出跟踪过程中的定位误差的实时曲线，如图2所示。

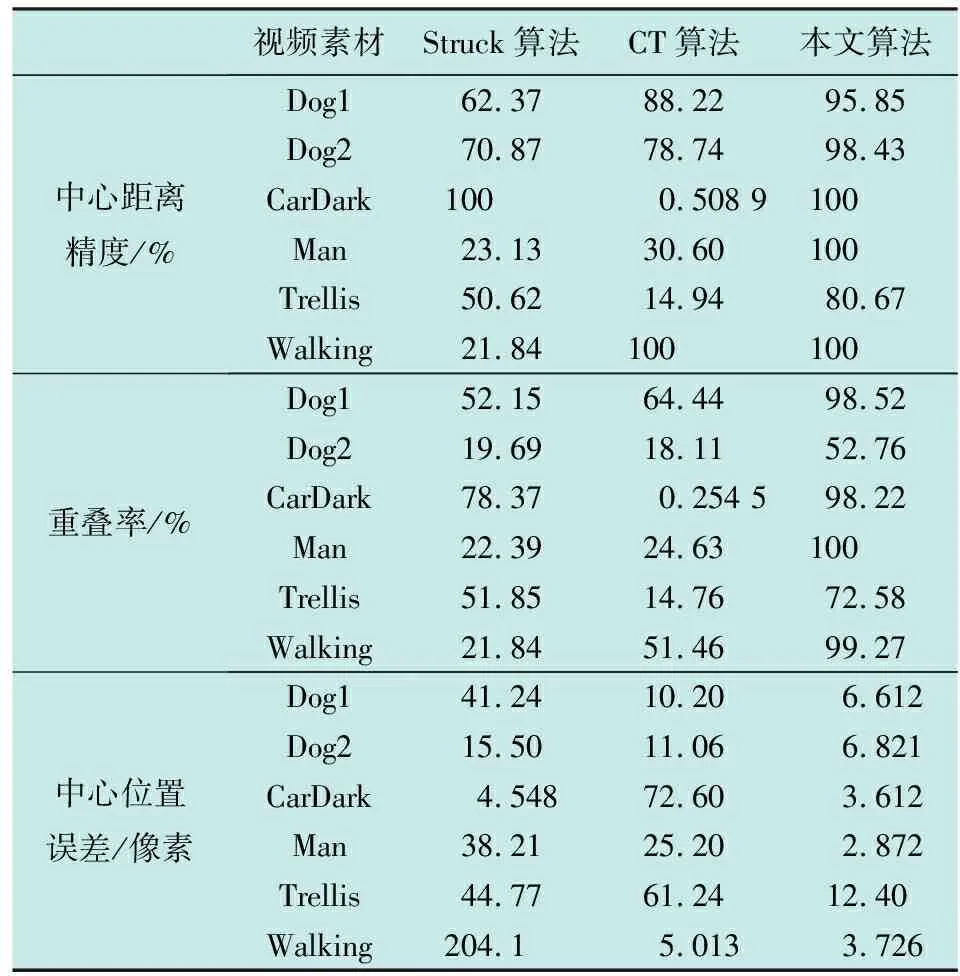
表2 中心距离精度、重叠率及中心位置误差

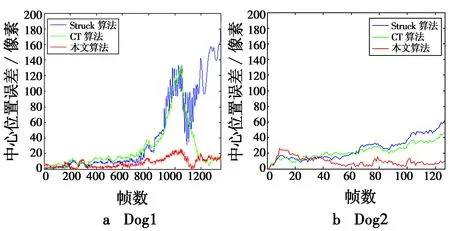
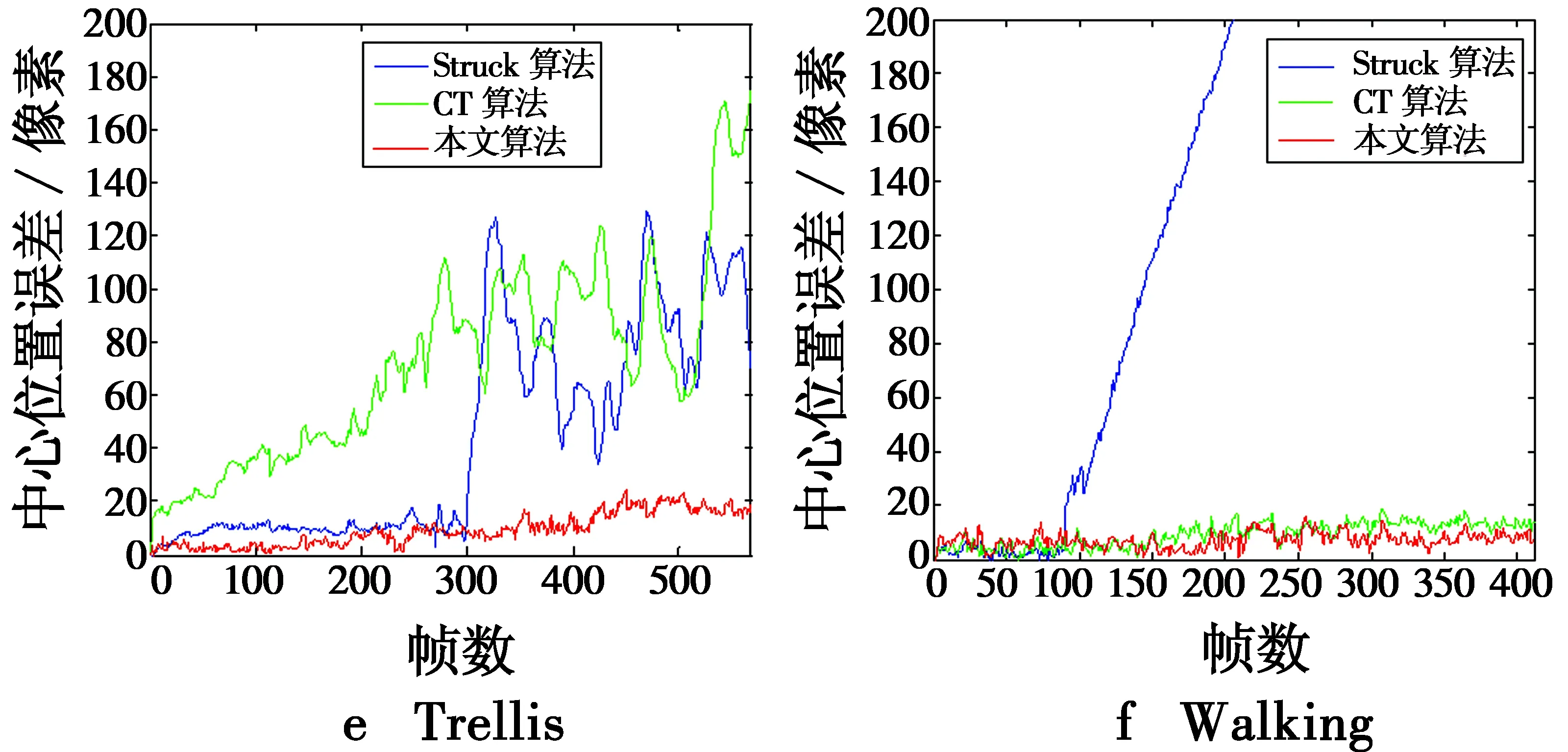
图2 各视频序列定位误差对比

表2及图2都是对本文所进行对比的3种算法针对不同视频序列的定量分析结果。实验数据表明，不论是从中心距离精度、中心位置误差还是重叠率方面来对比，本文算法性能都更加优越。本文算法取得了最低的中心位置误差，还取得了最高的中心距离精度和重叠率，只有Dog2序列的跟踪重叠率较其他序列低一些。在实时性上，以Dog1序列为例，在上述计算机配置环境下，图像像素大小为240×320，初始跟踪框像素大小为51×36，本文算法平均速度为13.49帧/s，虽然相比原始压缩跟踪算法64.4帧/s和Struck算法20.2帧/s的速度有所降低，但仍然满足准实时性要求。所以，本文算法整体跟踪效果优于其他两种算法。

5 结论

本文以传统的压缩跟踪算法为基础，提出了一种融合HOG类特征的尺度自适应压缩跟踪算法。由于融合了HOG类特征，大大降低了算法对光照变化的敏感度，而且加入了相关滤波尺度估计，能够适应目标尺度的变化，提高了跟踪算法的性能。实验表明，本文算法在跟踪难点如光照变化、平面内旋转、形变、相似背景干扰及部分遮挡下跟踪性能表现良好，具有较好的鲁棒性。算法虽然仍具有准实时性，但在原始CT算法基础上降速很多，所以在本文算法基础上继续提升速度是下一步的研究计划。另外，本文对于两类特征的融合采用了固定比值的融合方式，在保证算法实时性条件下两种特征的自适应融合也将是本文未来的研究方向。