舰载无人机着舰纵向控制律设计

赵东宏， 李春涛， 张孝伟

(1.南京航空航天大学，南京 210016； 2.成都飞机工业(集团)有限责任公司，成都 610091)

0 引言

自舰载机问世以来，着舰问题一直是各国研究的重点，而着舰末端的纵向轨迹跟踪控制更是成为着舰的最大难点。最初的着舰控制系统都是基于经典控制理论来设计的，这种常规的控制方法在复杂的环境扰动下对舰载机着舰精度的控制能力有限。随着现代控制理论和计算机技术的发展，一些先进的控制理论如动态逆控制、自适应控制等也逐渐应用于着舰，且表现出了良好的控制效果。文献[1]采用非线性动态逆滑模控制方法解决了飞行轨迹的精确控制问题；文献[2]设计了基于L1自适应控制方法的舰载机飞行控制系统，对高频和未建模动态进行抑制。目前，大多数着舰控制方案均是以发动机通道来保持迎角稳定，升降舵通道来调整着舰轨迹，此种方案在无人机受扰时同时操纵升降舵进行姿态与轨迹的调整，其内外环姿态与轨迹存在较强的耦合现象，不仅加剧了升降舵的操纵频率且不利于着舰轨迹的精确控制。

本文针对舰载无人机着舰时姿态与轨迹耦合的问题，提出了一种姿态与轨迹的解耦控制策略，采用升降舵通道保持着舰过程中姿态稳定，通过发动机通道来控制着舰过程的轨迹；并且应用了动态逆与自适应相结合的控制方法抑制未知扰动对控制系统的影响，保证控制系统的快速性与控制精度。

1 问题描述

无人机角动力学模型可描述为

(1)

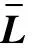
考虑到无人机存在建模不确定性(气动参数、结构参数等)与外界扰动等诸多不确定性因素，这些不确定性因素会带来额外的力矩变化，因此式(1)可改写为

(2)

式中：fp(xp),fq(xp),fr(xp),g(xp)分别为

(3)

(4)

(5)

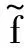
舰载无人机在着舰末端处于大迎角低动压的飞行状态，无人机的舵面效率下降，受复杂大气环境扰动时，易被激发出许多未知非线性特性，从而造成无人机力、力矩的畸变，再加上舰船本身的运动，使得轨迹跟踪更加困难[3]。无人机的这种状态可以用一个线性特征加有界扰动来描述，如纵向力矩方程可表示为

(6)

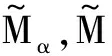
为了克服无人机大迎角受扰情况下激发的非线性特性，本文采用动态逆与自适应相结合的控制方法设计了以升降舵控制姿态、发动机控制轨迹的解耦控制律；应用动态逆控制消除系统中确定的非线性特性保证控制器的快速性，应用自适应控制消除系统中不确定性因素引起的未知非线性特性，保证无人机落点精确。纵向控制律结构如图1所示。

图1 纵向控制总体框架

2 升降舵通道控制器设计

2.1 俯仰角速率动态逆控制器设计

动态逆控制方法实质是采用全状态反馈抵消被控系统中的非线性部分，得到输入输出之间具有线性行为的新系统(称之为伪线性系统)，从而可针对伪线性系统进行控制律设计。

将式(6)整理为

(7)

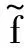
(8)

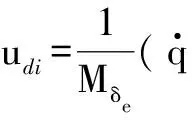
(9)

(10)

因此，俯仰角速率动态逆控制器为

(11)

选取样例无人机着舰状态下的典型工作高度为116 m，迎角为6°，指示空速为53 m/s，得到Mα=-1.53，Mq=-0.74，Mδe=-0.04。

根据控制器快速性要求，选取俯仰角速率回路指令模型的自然频率ωn=10 rad/s，阻尼比ξ=0.8，则可以得到指令模型的参数，其中,Kq=16，KI=100。图2所示为俯仰角速率动态逆控制器的时频域特性曲线，调整时间为0.5 s，相角裕度为80 dB，满足设计要求。

图2 俯仰角速率阶跃响应与开环伯德图Fig.2 Step response and Bode diagram of pitch rate

2.2 俯仰角速率自适应控制器设计

动态逆控制器前馈的特点可以满足着舰末端对控制器快速性的要求，但却无法克服系统中存在的未知不确定性。为此，本文采用自适应控制对系统中存在的不确定性进行在线辨识与估计，通过控制舵面偏转来消除由不确定性因素带来的系统动态变化，并应用投影算法确保其稳定性。

考虑

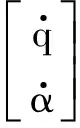
(12)

式中：V0为飞机稳定飞行速度；Zα，Zδe为力的量纲导数。

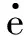
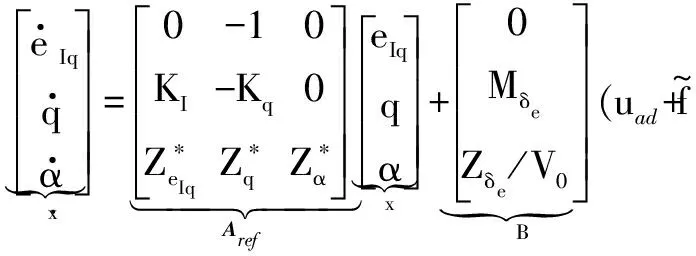
(13)

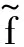
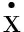
(14)

式中

(15)

因此，系统对不确定性因素的补偿输入估计为

(16)

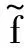
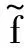
(17)

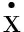
(18)

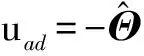
(19)

定义系统跟踪误差信号为e=x-xref，用式(18)减去式(14)，结合式(19)可以得到误差参考模型为

(20)

根据自适应理论，为使设计的自适应控制实现闭环稳定性，考虑如下全局径向无界的二次Lyapunov函数

(21)

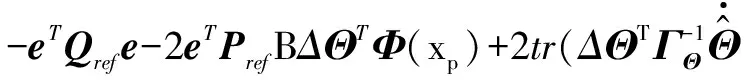
(22)

根据矢量迹恒等式aTb=tr(baT)将式(22)写为

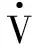
(23)

(24)

则可定义基于投影理论的自适应律为

(25)

(26)

(27)

图3所示为加入自适应控制前后的仿真结果。

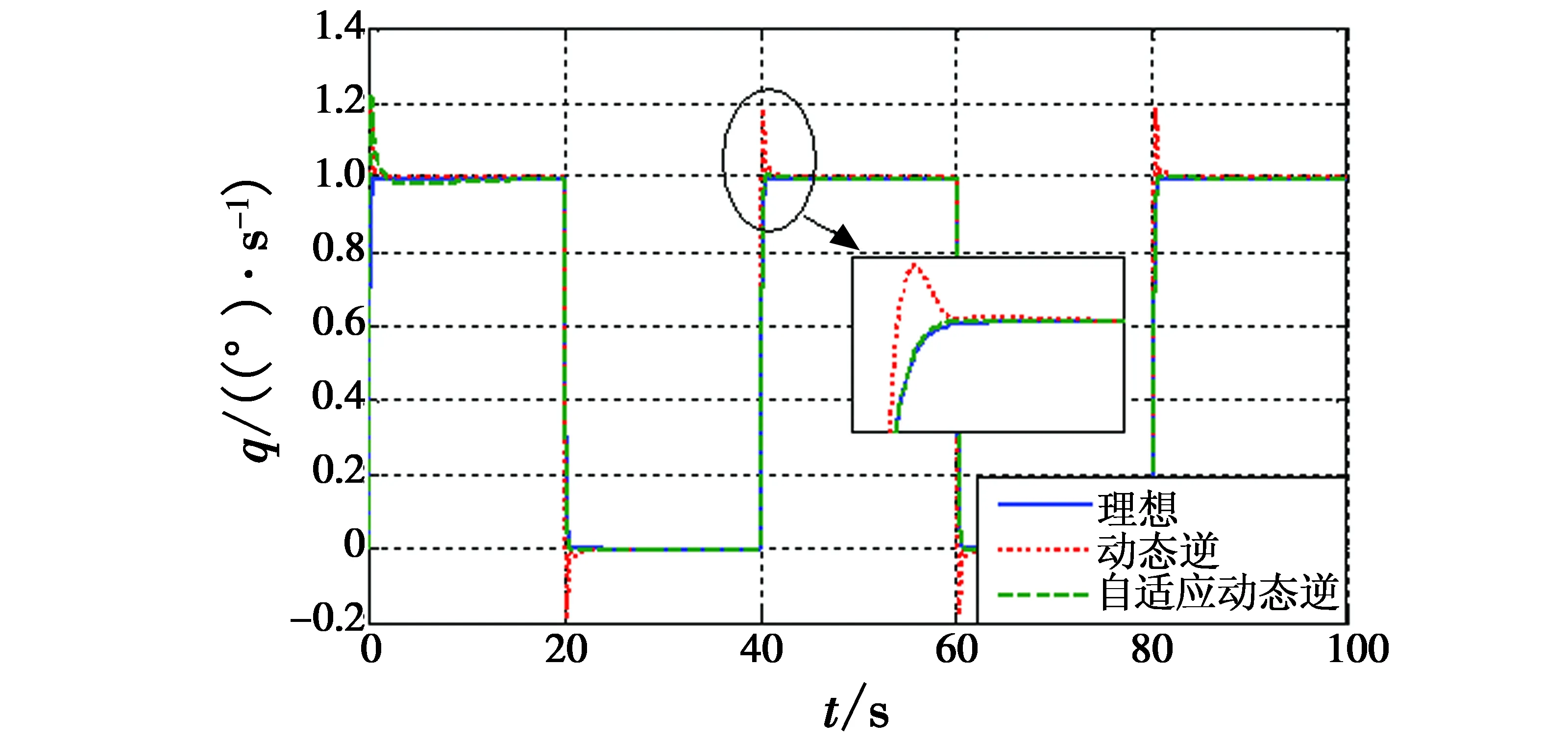
图3 (动态逆+自适应)控制器下的指令跟踪Fig.3 Command tracking with (DI+adaptive) controller

可以看出，当系统存在不确定性扰动时，动态逆控制品质变差，无法克服不确定性因素带来的系统振荡；加入自适应控制后，q的控制品质得到了明显的改善，实现了无静差跟踪。

2.3 俯仰角控制律设计

为防止无人机触舰时前轮先触地，着舰末端控制无人机跟随航母纵摇运动，且保证俯仰角预定指令大于舰船的纵摇运动幅值。本文在俯仰角速率内回路控制器基础上设计俯仰角控制器，根据无人机角运动学方程可得

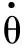
(28)

式中，φ为滚转角。

由于内回路已经确保俯仰角速率快速、无静差地跟踪指令，因此俯仰角控制器选择比例控制结构为

(29)

图4 俯仰角阶跃响应与开环伯德图Fig.4 Step response and Bode diagram of pitch angle

3 发动机通道控制律设计

在无人机着舰过程中,轨迹的控制是关键，为了避免着舰过程中无人机姿态与轨迹的耦合，本文采用发动机控制来实现无人机着舰轨迹的精确跟踪。

3.1 发动机通道控制飞行轨迹原理分析

大多数飞机具有速度稳定性，当速度受扰后会逐渐收敛，考虑方程

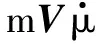
(30)

式中：V为飞行速度；T为推力；α为迎角；L为升力；θ为俯仰角。

无人机在稳态飞行的状态下，若油门受扰增大，会使飞行速度增加，升力增大，飞行轨迹向上弯曲；当油门扰动撤销后，由于速度稳定性的作用会使迎角增大，速度恢复至初始状态。整个过程是一个能量的转换过程，一般速度受扰后恢复时间较长，但若在姿态角可控的状态下，增大发动机油门会迅速改变无人机的飞行轨迹，使其在新高度下建立平衡状态。

3.2 发动机通道控制器设计

考虑方程

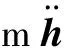
(31)

式中,D与μ分别为阻力与航迹倾斜角。

(32)

式中：m为无人机质量；az为法向加速度；Sw为机翼参考面积；CL为升力系数。

着舰末端的舰尾流会对无人机垂向速度造成1.0～2.0 m/s的扰动，这会使得无人机的轨迹跟踪性能变差，通过控制高度变化率的方法可达到抑制舰尾气流扰动的作用[6]，无人机在着舰过程中有

(33)

另外，为了削弱无人机俯仰角改变对高度轨迹产生的影响，本文将俯仰角的变化量作为前馈补偿项引入发动机通道，对升力进行补偿；综合考虑，发动机通道的控制器为

(34)

图5所示为高度阶跃响应与开环伯德图。表1所示为高度控制品质。

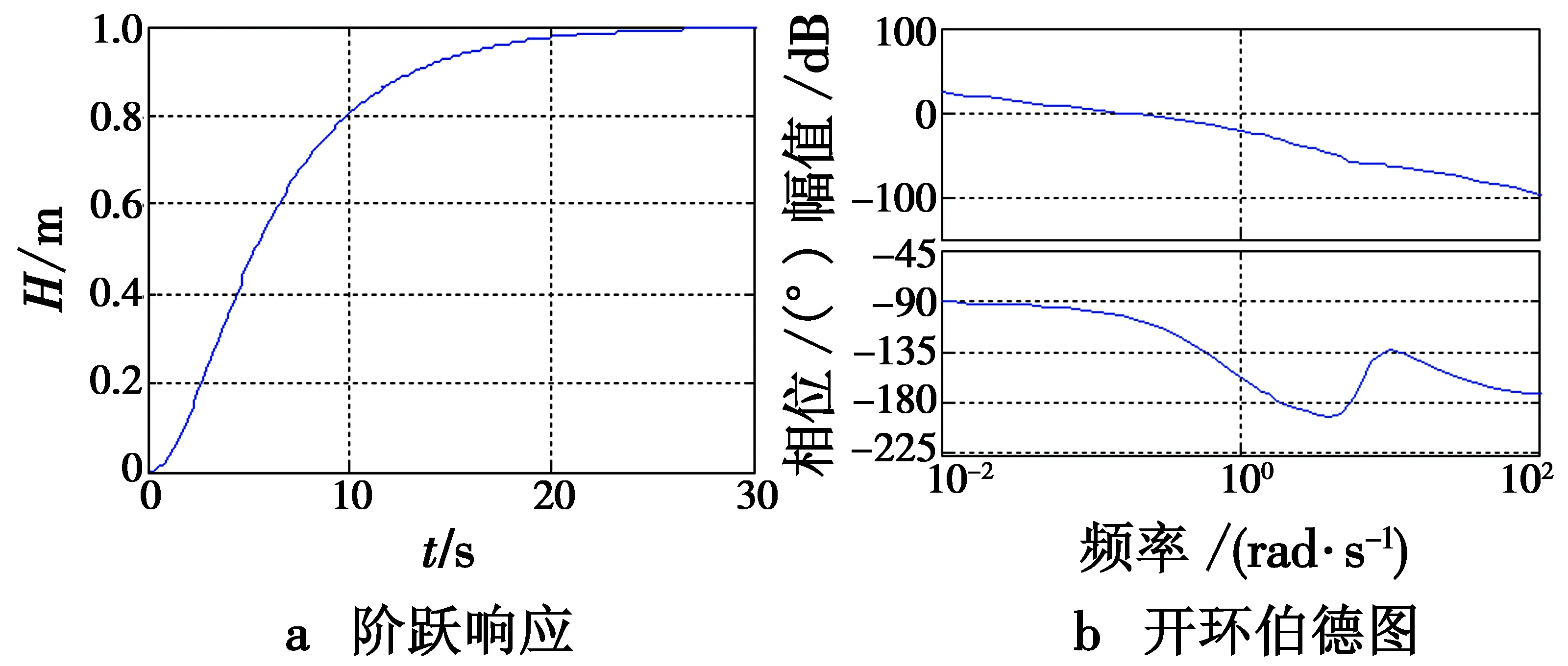
图5 高度阶跃响应与开环伯德图Fig.5 Step response and Bode diagram of altitude

上升时间/s系统带宽/(rad·s-1)幅值裕度/dB相角裕度/(°)80.3∞74.8

无人机在着舰末端能否准确跟踪舰船的沉浮运动，是决定着舰落点精度的另一个重要因素，该要求需无人机高度控制器的闭环带宽能覆盖舰船的运动频带。从图5及表1中可知，控制器的幅相裕度均满足设计要求，各频段频响特性良好，但控制器闭环带宽较窄，在舰船运动频率范围内(0.2～1 rad/s)存在一定的相位滞后，因此还需要设计甲板运动补偿网络来展宽控制系统带宽。

4 甲板运动补偿

根据不完全统计，舰船运动频率在0.2～1 rad/s左右[7]，由无人机高度闭环频率特性曲线可知，无人机在舰船运动频段内存在一定的相位滞后和幅值衰减特性，因此，需在发动机控制通道中引入甲板运动补偿器来展宽高度控制器带宽，以达到快速跟踪航母甲板运动的目的。加入补偿网络后的发动机控制系统结构如图6所示。

图6 甲板运动补偿网络Fig.6 Deck motion compensation network

图中：Hship为舰船垂荡高度；H为飞行高度。

补偿后的纵向控制系统在舰船运动频率0.2～1 rad/s内应满足

GDCM(s)GH(s)|s=jω,ω=0.2～1 rad/s=1

(35)

式中：GDCM(s)为补偿网络传递函数；GH(s)为高度回路控制器闭环传递函数。本文对甲板运动补偿网络的详细设计方法不再赘述，具体可参考文献[8-9]。样例无人机高度控制器闭环传递函数为

(36)

甲板补偿网络为

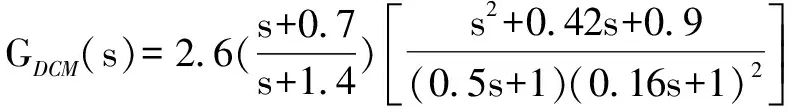
(37)

选取中等海况下甲板运动模型[10]，仿真验证甲板运动补偿网络GDCM的补偿效果，结果如图7所示。

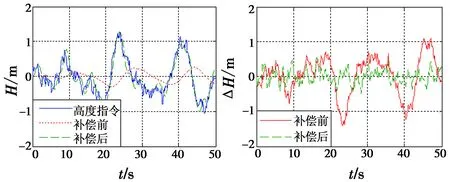
图7 甲板运动补偿效果Fig.7 Deck motion compensation effects

由图7可知，原控制系统高度跟踪误差范围为±1.5 m，加入甲板运动补偿网络后可以将高度的跟踪误差控制在±0.5 m内，显著提升了高度跟踪精度。

5 仿真验证

为了验证控制器的控制精度及控制效果，分别对舰载机在平静大气环境下与有舰尾流扰动的情况下进行着舰仿真验证。假设舰船以15 m/s的速度匀速前进，样例无人机初始高度为116 m，速度为53 m/s，沿-3.5°理想着舰下滑轨迹着舰。

1) 平静大气环境下着舰仿真。

由图8可知，舰载机在着舰下滑导引过程中俯仰角很好地跟随了指令给定；高度在切入下滑导引段时出现了约1 m的误差，之后随着下滑误差逐渐减小；在着舰末端，高度可以快速地跟踪甲板运动，触舰时舰载机俯仰角大于舰船俯仰角，实现了舰载机以安全姿态着舰，高度误差约0.4 m，满足着舰要求。

2) 穿越舰尾流着舰仿真。

为验证本文设计的控制器在舰尾流影响下的控制效果，在仿真系统中加入了舰尾流模型。仿真采用的舰尾流模型参照MIL-F-8785C军用规范中的规定，具体可见参考文献[11]。

图8 平静大气环境下着舰俯仰角、高度、高度误差曲线

图9 穿越舰尾流下着舰俯仰角、高度、高度误差曲线Fig.9 Pitch angle,altitude,and altitude error during landing with ship stern flow

从图9可以看出，舰载机在穿越舰尾流着舰时，其俯仰角及高度均具有良好的跟踪效果；受舰尾流扰动影响，在着舰过程中俯仰角与高度的波动较平静环境下的俯仰角与高度波动略大，但随着舰载机接近舰船，俯仰角与高度的跟踪误差均逐渐减小；触舰时，舰载机俯仰角大于舰船俯仰角，高度误差约为0.5 m，满足着舰要求。仿真结果表明，纵向控制器在一定程度上具有抑制舰尾流的作用，可以实现舰载机精确着舰的目标。

6 结束语

本文针对舰载无人机着舰过程中姿态与轨迹耦合问题，提出了姿态与轨迹解耦的新思路，详细地设计了姿态与轨迹控制器，并对控制器控制效果进行了仿真验证。仿真结果表明，该控制方法可以满足着舰落点误差的要求，且对舰尾流有一定的抑制效果，对着舰研究具有一定的参考价值。