戈壁滩地区输电线路掏挖基础上拔荷载应用

杨智峰，赵玉成，李占岭，赵怀宇，魏 锐

(1.石家庄铁道大学 交通运输学院，河北 石家庄 050043；2.河北省电力勘测设计院，河北 石家庄 050031)

掏挖基础在工程施工方法上，一般分为人工挖孔与机械扩孔；掏挖基础原状土的施工对周边环境影响不大，同时，能够有效保证土的承载力不被破坏。目前，掏挖基础应用较为广泛的是输电线路基础设施、高架桥梁等，一般地，工程上把不大于6 m的桩叫作墩，掏挖基础可以理解成扩底墩的形式。对于掏挖基础的研究，鲁先龙等在戈壁滩地区，以及黄土地区做过大量的工程实践。对输电线路杆塔基础的扩底墩而言，受力特性要优于直柱桩，对其他工程也有较好的借鉴与应用。

有限元模拟方法可以清晰地反映基础工程的受力特性，对于掏挖基础而言，建立三维弹塑性有限元模型能够更全面的、立体化的看到在上拔过程中的应力应变云图情况。ABAQUS软件在岩土工程领域应用较为广泛，能够解决岩土的非线性、参数数值化等问题，这里就掏挖基础的ABAQUS软件建模相对较容易，分析较具体；同时，对于岩土工程，通常采用MC模型，考虑边界问题等。

1 工程概况

某±800 kV输电线路穿过河西走廊戈壁滩地区，该地区海拔在1 300～1800 m之间，戈壁滩地表以砾石层为主，直径一般为2～5mm，成分大多为灰岩、页岩，颗粒级配较好，中粗砂、黏性土填充，混10%～20%卵石，戈壁滩雨水较少，土层自立性能较好。同时，沿线地下水位埋深超过10 m，对构筑物基础一般不造成影响。掏挖基础适用于硬塑土、可塑土的地质条件，以往对于戈壁滩碎石土质条件工程上应用较少，为此，进行有限元的模拟分析就显得尤为重要。根据已有的现场直剪试验，得到河西走廊的土质参数，粘聚力c值大约在10 ～20 kPa，土体有效摩擦角φ在40°～47°。

2 有限元建模分析

2.1 土的力学模型

在岩土中M－C模型应用较多，图1摩尔圆中，表示正应力σf与切应力τf的关系式为：

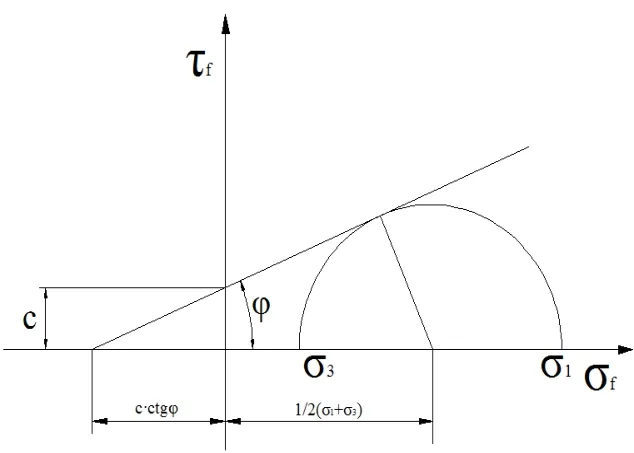
图1 摩尔圆示意图

在ABAQUS模拟中，塑性势面形式采用连续光滑的塑性势函数来修正摩尔库伦里菱角分明的屈服面，使计算更容易收敛。

2.2 桩土本构关系

掏挖基础的有限元三维建模，采用八节点六面体单元，基础尺寸桩身直径d为1.30 m，扩底直径D为1.85 m，扩底矢高为0.8 m，桩长L为4.6 m，满足人工挖孔的要求；为了最大程度上消除边界对上拔过程的影响，这里选取土体半径为15倍扩底直径，3倍的桩长；考虑到桩土耦合作用，选取一半建模并不影响计算结果；钢筋－砼桩等效为相同强度的线弹性体，土为非线性的弹塑性体符合Mohr－Coulomb屈服准则，具体桩土参数见表1。

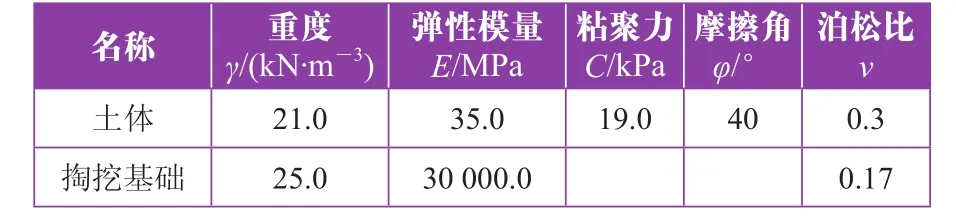
表1 桩土材料参数

2.3 建模过程分析

根据桩土的本构关系建立计算模型，见图2。

图2 掏挖基础计算模型

桩土接触问题是有限元分析的关键，本文考虑单桩受极限上拔荷载的情况，桩的侧摩阻力τ=μp，其中，摩擦系数μ的取值与土的内摩擦角有关，这里采用μ=tan(0.57φ)，p为接触面的竖向土压力与横向系数K0(K0=1－sinφ)的乘积；工程中，通常在现场绑定钢筋笼及浇筑混凝土施工，可保证桩良好的强度，且使桩土接触更紧密，因此，在有限元建模中，可以采用桩土的面面单元接触，桩的强度大且网格划分较密作为主面。

桩土边界采用底部在空间三维约束，桩土的对称面以及土的外侧进行水平向约束，方便进行竖向荷载施加与位移观测，且符合工程实际。在桩顶面逐级施加静力荷载，首次可选择2倍预测极限值的1/10进行施加，为了精确地得到所求极限荷载值，这里采用尽可能小的单级荷载值，多分析步的计算方法。

桩土网格划分越精确对计算结果越有益，这里设置桩土为非独立单元，共享一个接触面节点，桩土一共拥有10998个单元，见图3。

IgD型MM的治疗方法与其他类型的骨髓瘤相似，以化疗和自体造血干细胞移植为主[1, 5-6,11]。在应用硼替佐米、来那度胺等新药及进行自体干细胞移植治疗之前，IgD型MM患者的中位生存期不足2年[6]；另有文献[12]报道，这类患者的中位生存期只有21个月，3年及5年的生存率分别是36%、21%。大剂量化疗后联合自体干细胞移植可以改善患者的总体生存率，延长其无病生存时间[8, 13-15]。研究[13]表明，单纯化疗患者的疾病总体生存期可达2年，化疗加自体干细胞移植患者总体生存期可达5.1年。

图3 桩土网格划分示意图

计算过程分析，第一步采用自动地应力平衡法，对土施加重力构建应力场，满足自然条件下土体位移为0的状态；第二步添加桩，并设置桩土的接触，同时对桩施加重力荷载以满足工程实际存在自重的状态；第三步后，对桩逐级施加荷载，以有限元计算最终尽可能收敛为止。

2.4 数据处理分析

得到相应的桩顶荷载与位移曲线关系(QS)，见图4。依据规范极限荷载值为3250 kN。通过表2有限元计算值、公式推导值、现场试验值分析可见，有限元模拟值为“剪切法”值的79.50%，为现场试验值的59.09%，偏于安全。

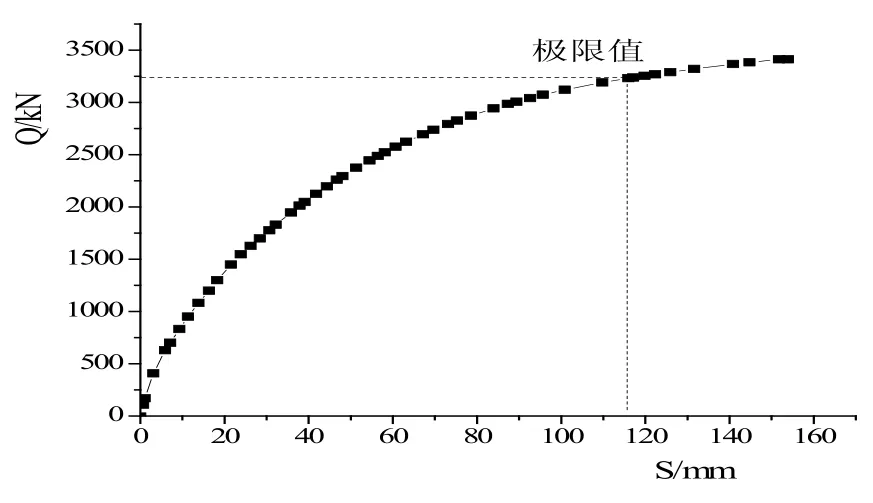
图4 桩顶荷载与位移曲线关系图

表2 计算结果对比表

在桩处于极限荷载情况下，土体表面、桩体中部及距扩底端以上0.4 m处的位移曲线见图5。较大位移出现在扩大头斜截面中部，是桩侧地表面位移的3～4倍；从图中可见，距离桩侧10 m以上，土体竖向位移已达10～4 m以上，满足桩土边界计算的位移场要求。

图5 桩侧土边界范围内位移变化图

根据侧摩阻力经验计算公式，

(其中，γ为土体容重，z为桩深)，计算等截面4.6 m桩的侧摩阻力值为433.34 kN。有限元计算基础上拔荷载传递见图6，荷载在小于(等于)500 kN时，桩身侧摩阻发挥作用，等同于等截面桩桩身荷载传递效果；超过该值时，桩身在变截面处出现荷载走势突变的情况，说明扩大头起到明显抵制上拔荷载的作用。

图6 桩身荷载传递曲线关系图

桩在受不同上拔荷载时，土体的塑性变形情况见图7～图9。受影响土体的范围随着荷载增大沿着桩身向上延展，在荷载值为1000 kN时，塑性变化出现在变截面处及桩底，土体有少许屈服；逐级荷载施加到2000 kN时，土体塑性屈服面沿着距扩底端边缘外0.9 m处呈柱状向上延伸，在距地表面1.9 m处呈倒锥形，为“复合型”破坏形式；荷载继续加大时，地表距桩侧5.14 m内，呈“倒台锥型”破坏，土体完整的屈服面形成，整体剪切破坏形式符合规范要求。

图7 1000 kN时桩周土体塑性屈服变化图

图8 2000 kN时桩周土体塑性屈服变化图

图9 3250 kN时桩周土体塑性屈服变化图

3 掏挖基础上拔荷载影响因素分析

3.1 土体内摩擦角的影响

土体有效摩擦角的改变，理论上桩土接触面的摩擦系数会有相应的变化，这里固定取系数为0.58，考察其对桩上拔承载力的影响。不同摩擦角下的荷载－位移曲线关系见图10。

通过对比分析，土体内摩擦角对桩上拔承载力有较大影响。内摩擦角40°的土体承载力为内摩擦角30°的1.44倍，说明土体随着内摩擦角值的增大而拥有较好的抵制上拔承载力。

3.2 土体弹性模量的影响

土体弹性模量选取为0.6Ec、1Ec、1.5Ec(Ec为上文模拟土体的弹性模量)时，基础的承载力情况见图11。由图可见，土体模量对基础的上拔承载力影响较大。

图10 不同φ值下的荷载－位移曲线关系图

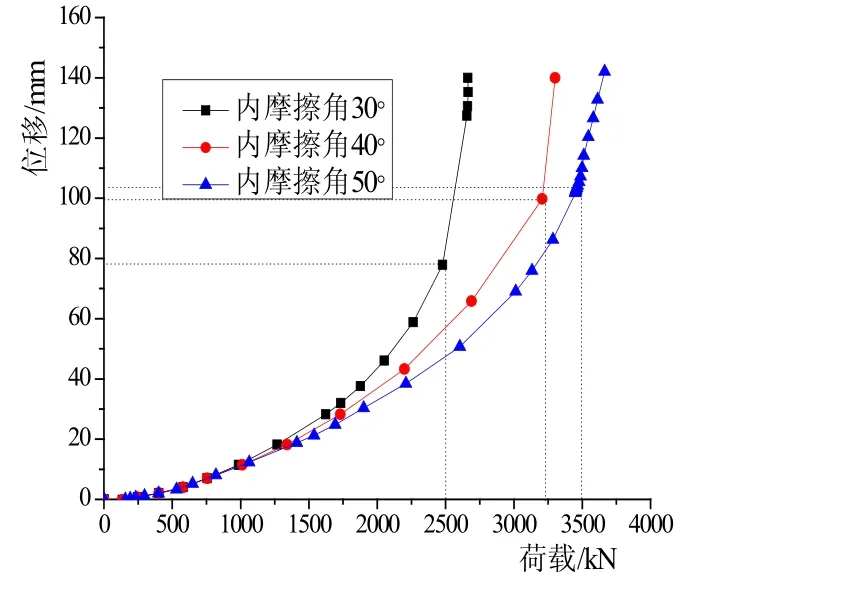
图11 土体模量变化下的荷载－位移关系图

3.3 桩长的影响

桩长选取为0.8L、1L、1.3L(L为上文模拟桩长)，通过桩顶荷载－位移曲线关系图12可得，上拔极限荷载值随着桩长的增加而增加，1L桩长为0.8L桩长承载力的1.625倍。工程中一般地考虑建(构)筑物的设计上拔极限荷载值，从而选取适宜的桩长，降低工程造价，节约资源。该工程根据实际地质勘测及几何尺寸最优化设计采用直线塔2.9 m≈0.63L埋深，转角塔4.1 m≈0.89L埋深。

3.4 扩底矢高的影响

扩底高度对基础构造有一定影响，改变了扩展角度。选取0.8h1、h1、1.3h1进行三维有限元模拟得到相应基础荷载情况见图13。扩底圆台高度增加，相应地扩展角减小，随之基础上部覆土减少，承载力值也随之降低。一般地，掏挖基础在设计与施工开挖过程中，都要注意变截面处的角度问题，防止圆台上部土体坍塌，对于戈壁滩特殊土质，该基础工程控制扩展角度在≤20°范围内。

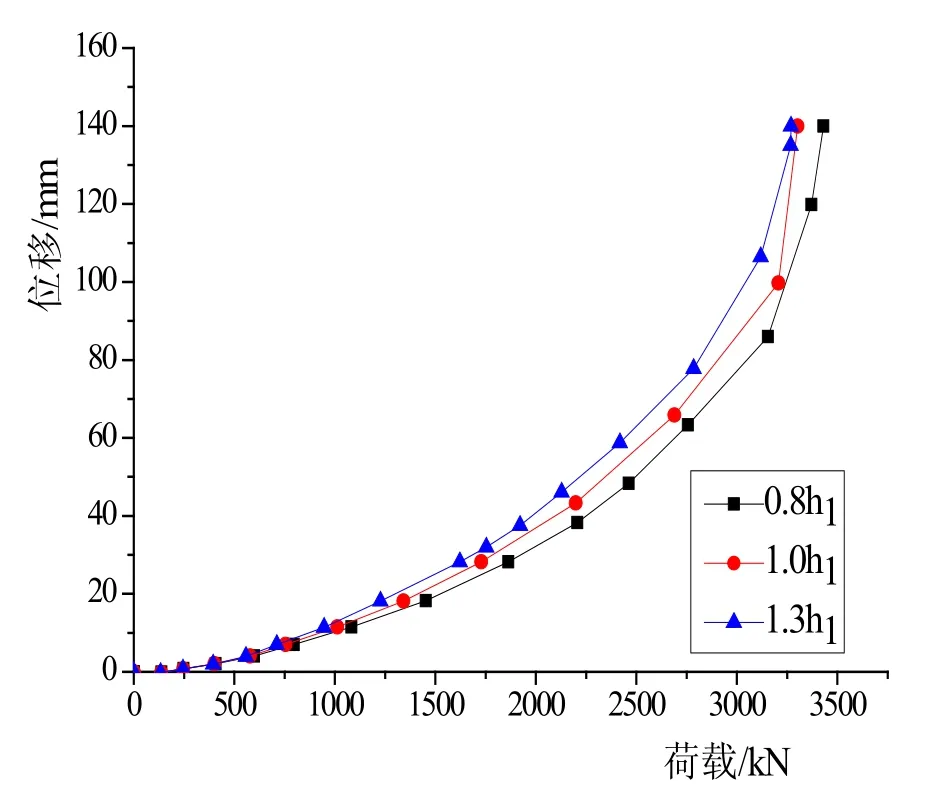
图12 不同桩长下的荷载－位移曲线关系图

图13 土扩底矢高变化下的荷载－位移关系图

4 总结

(1)通过三维有限元将桩土参数数值化，得到的模拟极限荷载值低于工程实测值，略保守；掏挖基础上拔荷载的传递机制较为明显，随着荷载值的增大沿着桩身向下延展，扩底圆台的扩展角起到关键作用。

(2)掏挖基础的破坏形式为“倒台锥型”破坏，地表影响范围为距桩侧5.14 m≈4d；桩土本构模型的边界条件，距桩侧10 m≈5.41D处以上即可。

(3)掏挖基础保留原状土体的承载力，对周边环境影响不大；影响其上拔承载力的因素中，内摩擦角、土体模量、桩长都与承载力值成正比关系，圆台高度会影响到扩展角的改变，同时，立柱与扩底直径对扩底桩也有较大影响。