邹城市西苇水库月降水量时间序列分析

梁玉荣，甘信娟，聂圣菊

（济南市水文局，山东 济南 250014）

西苇水库是一座以防洪、灌溉为主，兼顾发电及渔副业生产的大型水库。该水库建成于1960年6月，总库容1.02亿m3，控制流域面积113.6 km2。2002年，西苇水库经除险加固后，已能有效控制洪水，如遇千年一遇大洪水，大沙河流量将由1 670 m3/s，消减至376 m3/s，对减轻下游洪涝灾害，确保京沪铁路、邹县电厂、兖州煤矿及人民生命财产的安全，起到极为重要的作用。本文采用1961—2015年长达54年的实测降水观测资料，以西苇水库的月实测降水量为研究对象，采用指数平滑模型，自回归滑动平均（ARIMA）模型对数据进行研究。

1 研究方法

1.1 指数平滑法

1976年布朗提出指数平滑算法，该方法提出稳定性或规则性是时间序列固有特性，可以用最近的过去态势来合理地顺势推延相关的未知时间序列。该方法重点关注最近的资料。在生产预测中，指数平滑法是用得最多的中短期数据发展趋势预测方法。指数平滑公式分别为：

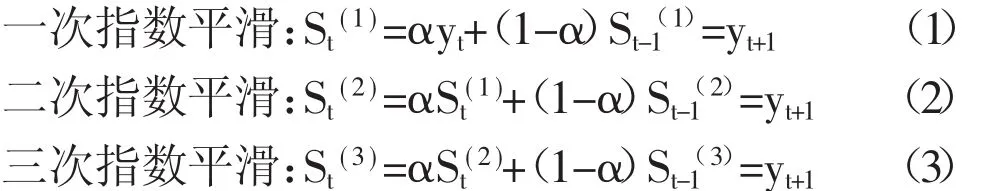
上标（1）、（2）、（3）分别代表一、二、三次指数平滑，α为平滑系数，取值为0～1。

1.2 自回归滑动平均（ARIMA）模型

70年代初博克思（Box）和詹金斯（Jenkins）提出了自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model，简记 ARIMA，又称Box-Jenkins模型、博克思-詹金斯法），它是一种有效时间序列预测方法。在差分自回归移动平均模型 ARIMA（p，d，q）中，AR 代表自回归，p是其中的自回归项；MA代表移动平均，其中q为移动平均项数，时间序列中需要d次差分才能成为平稳的序列，使用该方法可以把非平稳时间序列进行平稳化处理，然后建立因变量与它的滞后值以及随机误差项的现值和滞后值之间的函数。模型为：

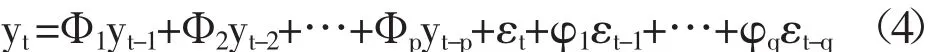
其中，自回归系数为 Ф1，Ф2，…，Фp；自回归阶次为 p；滑动平均系数为 φ1，φ2，…，φq，滑动平均阶次为q；白噪声序列为εt。若进行d次差分，则记为 ARIMA（p，d，q）。

ARIMA模型预测的基本程序：首先依据散点图、自相关函数和偏自相关函数图来识别降水量序列的平稳性，接着进行平稳化处理降水量序列，选择不同的模型，根据参数估计来检验序列的统计意义，根据假设检验来判断残差序列是否为白噪声，利用已通过检验的模型进行预测分析。

2 数据处理过程及结果

2.1 指数平滑模型

对西苇水库水文站1961—2015年月降水量时间按序列数据进行指数平滑法分析，从自相关（ACF）和偏相关（PACF）序列图可以看出：残差相关序列并没有显著的趋势特征，因此，利用该模型进行分析预测存在一定的合理性。

图1给出了观测值和拟合结果。图中的虚线为预测的2016—2020年月降水量，从图中可以看出，月降水量呈周期性变化，周期数为12个月，每年7月最大降水量为200 mm左右。但是该模型预测的降雨量数值是固定的序列，这与实际不大相符，但能大概反映出月降水量的大致变化趋势。

图1 观测值和指数平滑法拟合结果

2.2 自回归滑动平均（ARIMA）模型

根据西苇水库水文站1961—2015年月降水量时间按序列数据进行模型处理，首先判断，时序是否平稳，未经差分处理的降雨量ACF图见图2，由图2可以看出超过一半的自相关系数未进入置信区间，说明该序列非平稳，需要进行差分处理。

图2 未经差分处理的降雨量ACF图

对时间序列进行差分平稳（差分选d=1），绘制相关系数图见图3，由图3可以看出在k=12之后，自相关函数衰减，并且基本在置信区间范围之内，可以认为该序列平稳了，其中Ф12，12=0.345最大，其他并没有明显趋于0，可以认为在k=12后拖尾。因此经过一阶差分后的降雨量入选模型为 ARIMA（12，1，12）或 ARIMA（0，1，12）。分别对两个模型进行拟合和预测，比较其精度。

图3 差分平稳（d=1）后的相关系数图

表 1 分别给出了 ARIMA（12，1，12）和 ARIMA（0，1，12）的统计数据，由表可以看出ARIMA（12，1，12）模型的R平方和平稳的R平方优于ARIMA（0，1，12），因此可以认为 ARIMA（12，1，12）模型的结果更为可信和准确。

表1 模型统计资料

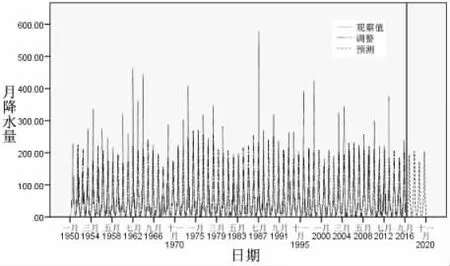
图4 ARIMA（12，1，12）模型的观测值、调整值和预测结果

图4 给出了ARIMA（12，1，12）模型的观测值、调整值和预测结果。图中的虚线为预测的2016-2020年月降水量曲线，由图可以看出使用 ARIMA（12，1，12）模型计算得到的月降雨量（调整值）基本与实测月降雨量相符，说明该模型可以从理论上对西苇水库的月降雨量进行分析和预测。假如在预测的过程中不断使用最新数据，并调整模型，则模型的理论和实用价值会更大。