基于期限约束与关键路径的云工作流调度

刘雨潇, , ,

(湖北文理学院 数学与计算机科学学院,湖北 襄阳 441053)

0 概述

云计算可以融合大规模计算能力应用于实际问题求解,如工业、医疗、商业和科学计算等领域。就调度而言,以上领域的应用通常涉及复杂且多阶段的操作处理过程,即工作流模式[1]。云计算正是通过其弹性的资源提供模式及即付即用的资源支付方式,使得各领域下的工作流任务可以高效完成,类似Globus Galaxies平台[2]的云工作流应用正使得云计算环境成为构建科学工作流调度与分析的主流方法。

将工作流调度至可用资源,同时满足任务依赖关系及用户定义的相关服务质量(Quality of Service,QoS)约束即为工作流调度问题,通常为NP-完全问题。云资源上的工作流调度包括2个阶段:资源提供与任务调度[3]。资源提供阶段旨在决定任务所需资源的类型和数量,并预留至工作流执行。工作流任务调度阶段旨在决定任务最优执行序列和满足用户与工作流约束的任务部署[4]。目前的研究工作多集中于第二阶段,即对于预定义的资源池(通常为同质资源),以最小化工作流执行时间为目标,未考虑资源使用代价。

本文提出一种基于期限约束与关键路径的云工作流调度算法,用于动态云资源提供环境中的调度优化。作为一种线性启发式调度方法,该算法包括2个阶段:任务优先级确定和任务分配。第1个阶段为各个工作流任务分配升秩/降秩值,并基于秩值和对任务进行调度排序;第2个阶段则寻找最优执行资源。本文通过两阶段的工作流调度,实现期限约束下工作流执行代价的最小化。

1 相关工作

在独立型包任务与依赖型工作流任务调度领域中,常见算法有启发式算法、搜索算法和元启发式算法。任务至资源间的分配可划分为调度阶段和提供阶段。传统的GAIN算法[5]可归类为纯任务调度阶段的算法,而DRIVE算法[6]更侧重于资源提供阶段。仅考虑某一阶段的优化通常较适用于传统的分布式计算环境,而云调度系统则同时包含了调度与提供2个阶段。

工作流调度算法有2个主要的分类:尽力服务调度与QoS约束调度[7]。尽力服务调度算法的目标是最小化工作流执行跨度makespan,如HEFT算法[8]、Suffrage算法[9]、Min-Min算法[9]和Max-Min算法[9]等,这类算法通常忽略执行代价因素,并不符合云资源的使用特征。QoS约束调度算法主要是在满足用户定义的相关约束的条件下优化QoS参数,如考虑预算约束算法[10]和考虑期限约束算法[11]。相比尽力服务调度算法,QoS约束调度算法更适应于现实世界中科学工作流的应用特征。然而,该类算法在约束条件和优化较多时,会因较高的时间复杂度而不具实用性。

元启发式算法是解决多约束调度的常用方法,如遗传算法GA[12]、蚁群优化算法ACO[13]和粒子群优化算法PSO[14-15]等随机搜索算法。该类算法可以通过种群初始化和大量解空间,以较高的时间代价求解云环境中的有效调度解。然而,该类算法寻找可行调度解时的开销会随着工作流规模的增加而增大,因此,在面对复杂大规模的实时工作流调度时效率不高。

在与本文类似的其他相关研究中,文献[16]提出一种基于局部关键路径的调度算法IC-PCP,算法目标是满足截止时间约束下最小化执行代价。该算法将处于局部关键路径的所有任务优先调度至费用最低的资源上,避免每个PCP上的通信代价,但算法忽略了资源的启动和部署时间。文献[17]在IC-PCP算法的基础上,提出增强算法EIPR,利用资源预分配空闲时间和预算盈余进行任务复制,以降低代价。然而,该算法会因为任务复制增加用户代价。文献[18]提出一种分割平衡时间调度算法PBTS,在满足期限约束的同时最小化执行代价,算法主要通过估算所需资源的最小数量最小化执行代价。文献[19]提出一种满足给定预算和截止时间约束的最大化工作流执行数量的算法。然而,与本文算法相比,该算法仅考虑了一种资源类型,本文则考虑了多类型的资源使用实例。文献[20]提出一种满足期限约束的动态代价最小化算法JIT,将管道任务集合并为单个任务以降低协作任务间的数据通信代价,但该算法并未优化目标资源寻找过程。

2 问题模型与定义

本文以有向无循环图(Directed Acyclic Graph,DAG)表示工作流,定义为G=(T,E)。其中:T表示图的节点,即任务集;E表示图的有向边,即任务间的依赖关系集;边ei,j∈E表示任务ti与tj间的有向边,即执行顺序约束,仅当完成任务ti并接收ti的所有数据后,才开始执行tj,此时,ti称为tj的直接前驱或父任务,tj称为ti的直接后继或子任务。在工作流DAG中,每个任务可拥有一个或多个父任务或子任务,仅当ti的所有父任务完成后,ti才可以开始执行。若任务没有任一父任务,则称该任务为DAG的入口任务(entry task);若任务没有任一子任务,则称该任务为DAG的出口任务(exit task)。若工作流DAG拥有多个入口或出口任务,为了确保DAG仅有单个输入与输出路径,通常增加2个傀儡任务作为入口任务tentry和出口任务texit,且傀儡任务的执行代价及与其他任务间的通信数据均为0。

在云环境中调度工作流时,用户通常会提供相应的QoS约束,本文考虑工作流执行的期限约束Duser和执行代价cost,优化目标是在满足期限约束的同时,追求工作流执行代价的最小化,形式化为:

其中,makespan表示整个工作流的执行时间。

3 WS-DCCP算法设计

3.1 任务优先级确定

将所有工作流任务根据并行程度和同步需求划分为不同的逻辑层次(level)。为了最大化任务的并行程度,在划分任务分层时,考虑同一层次中的任务间不存在依赖性,从而使每一层次可考虑为包括独立任务集的包任务。定义一种向下分层法对任务进行分层,即定义任务ti的分层为任务ti至出口任务之间路径的边的最大数量,如图1所示。

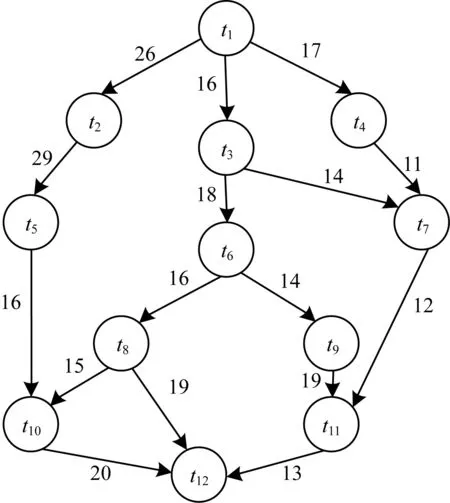
图1 工作流DAG

在图1中,边上的值表明任务间的通信时间(代价),分层表明任务所处的任务包(Bag of Tasks,BoT)。对于出口任务,其分层恒为1。对于其他任务,分层计算方式为:

其中,succ(ti)表示任务ti的直接后继集,levelnum(ti)表示任务ti所在层数。

根据任务分层,将所有拥有相同分层的任务组成任务分层集合TLS,即:

TLS(l)={ti|levelnum(ti)=l}

(3)

其中,l表示分级数,且l∈[1,2,…,levelnum(tentry)]。

3.1.1 正比例期限重分配

任务分层后,需要将工作流期限Duser以正比例方式在各个分层上进行重分配。令levelsub-deadline表示单个分层的子期限。为满足全局期限Duser的约束,需要确保单个分层中每个任务在其分配的子期限内完成。

首先,定义每个分层l的初始子期限估算值为:

在式(4)中,ECT(ti)为任务ti在所有资源上的最早完成时间,定义如下:

(5)

其中,pred(ti)表示任务ti的直接前驱集,exemin(ti)表示任务ti的最小执行时间,ACTi,k表示任务ti与其父任务tk间的平均通信时间,ltk表示父任务ti的分层。由于入口任务tentry没有父任务,因此ECT(tentry)=0。

式(4)表明,一个分层中所有任务的最大ECT可视为该分层的全局完成时间估算值,该时间可作为所处分层中所有任务并行执行时要求的绝对最小完成时间。

然后,基于每个分层的期限长度,将以上比例加至每个分层中:

(7)

显然,拥有越长任务的分层将得到越长的期限分配。

3.1.2 约束关键路径

定义1(关键路径) 工作流DAG中入口任务至出口任务间的最长路径称为关键路径(Critical Path,CP)。

定义2(关键路径的长度) 表示工作流DAG的关键路径上任务的计算时间与通信时间之和,即调度工作流的时间下限。

定义3(约束关键路径) 仅包括就绪任务的任务集构成的路径称为约束关键路径(Constrainted Critical Path,CCP)。

定义4(就绪任务) 若某任务的所有父任务已经执行,且所有数据均已接收,则称该任务为就绪任务。

传统方法基于升秩和降秩的方式寻找工作流DAG的所有CCP。任务ti的升秩表示从任务ti至texit间的关键路径的长度,定义为:

其中,AETi表示任务ti的平均执行时间,ACTi,j表示任务ti的平均通信时间。从式(8)可以看出,任务的升秩需要从出口任务开始计算,然后递归计算至工作流DAG的入口任务。对于出口任务texit:

rankup(texit)=AETexit

(9)

任务的降秩需要从入口任务开始计算,然后递归计算至工作流DAG的出口任务,定义为:

(10)

同时,有:

rankdown(tentry)=0

(11)

rankdown(ti)表示任务tentry至任务ti的最长距离,但不包括任务本身的计算时间,而rankup(ti)则表示任务ti至texit间关键路径的长度,包括任务本身的计算时间。

WS-DCCP算法对任务升秩与降秩计算方式进行改进,如式(12)和式(13)所示。

(12)

rankdown(tk))

(13)

与传统方法不同,改进升秩与降秩计算任务的前驱或后继任务的通信时间总量而不是选择其中的最大值。通过这种方式,可以使得拥有更高出度或入度的任务拥有更高的优先级,从而使得该类任务优先被执行,且在下一条约束关键路径CCP上的更多任务可被置为就绪任务。

同时,WS-DCCP算法通过任务的升秩与降秩之和寻找所有工作流DAG的关键路径:

ranksum=rankup+rankdown

(14)

首先,基于任务的ranksum值对所有任务进行排序;然后,将拥有最高ranksum值的任务选择为第一条关键路径。第一条关键路径上的所有任务标识为已访问任务,以同样的方式,可以找到工作流的所有关键路径。该过程的执行步骤如算法1所示。

算法1关键路径查找算法

输入工作流G=(T,E)

输出关键路径

1.procedureFindCP(DAG G)

2.for all task ti∈G do//遍历工作流的所有任务

3.calculate rankup,rankdownand ranksum//计算各任务秩值

4.end for

5.CPlist←Ø//初始化关键路径列表为空

6.while there is an univisited task in G do//寻找未访问任务

7.ti←biggest ranksum//寻找最大秩值和

8.CP←Ø//置关键路径为空

9.while tiis not null do

10.add tito CP//添加任务ti至关键路径

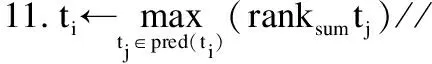
12.end while

13.add CP to CPlist//添加关键路径至关键路径列表

14.end while

15.end procedure

3.1.3 算例说明

本节以一个实例,分别说明传统升秩与降秩方法和WS-DCCP算法的改进秩值方法寻找约束关键路径CCP的不同。考虑图1所示的工作流结构,边上数值代表任务间的数据通信时间,每个任务的平均计算时间AETi、升秩值rankup、降秩值rankdown以及升降秩值之和ranksum如表1所示。

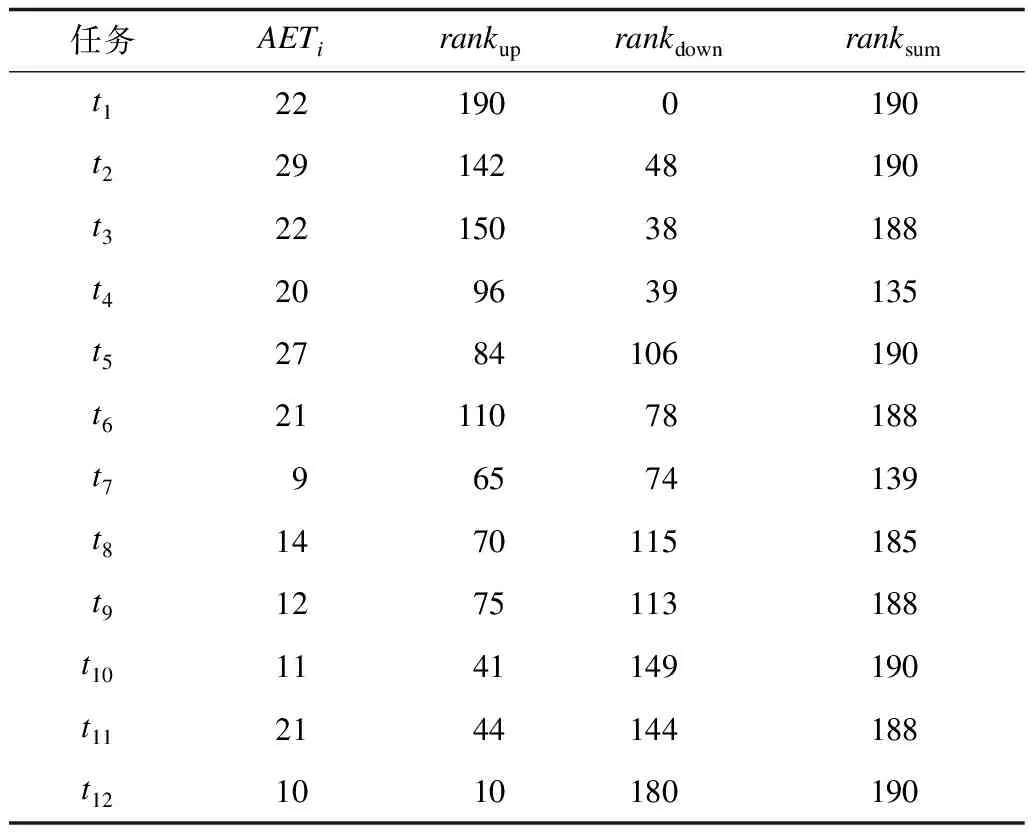
表1 各任务计算时间、标准升降秩及其和

首先,根据选取任务ranksum最高的原则,可以得到第一条关键路径为t1→t2→t5→t10→t12;然后,剔除已访问的第一条关键路径中的任务,以同样的ranksum最高原则,可依次得到其他关键路径;最后,需要通过遍历关键路径CP,以循环方式寻找约束关键路径CCP。在第1条CP中,仅有任务t1、t2可就绪,其他任务均无法就绪,则第1条CCP为t1→t2。例如:考虑第1条关键路径中的任务t5,该任务未添加至该CCP,由于其父任务之一t3仍未添加至任意CCP中。当无法在第1条CP中找到更多的就绪任务时,即可考虑通过第2条CP建立新的CCP。在第2条CP中,由于任务t3的唯一父任务t1已经添加至第1条CCP中,则任务t3为就绪任务。依此类推,可知第2条CCP包括3个任务:t3→t6→t9。从第2条CP中排除任务t11的原因在于它的一个父任务t7仍未添加至任一CCP中。同理,其他的CCP可利用剩余的CP进行构造。通过上述过程得到的CP与CCP如表2所示。

表2 通过标准升降秩得到的CP与CCP

基于同样的CP和CCP构造方法,改进的任务升秩与降秩值及得到的CP和CCP如表3和表4所示,其中,AETi表示每个任务的平均计算时间,rankup表示改进升秩值,rankdown表示改进降秩值,ranksum表示升降秩值之和。

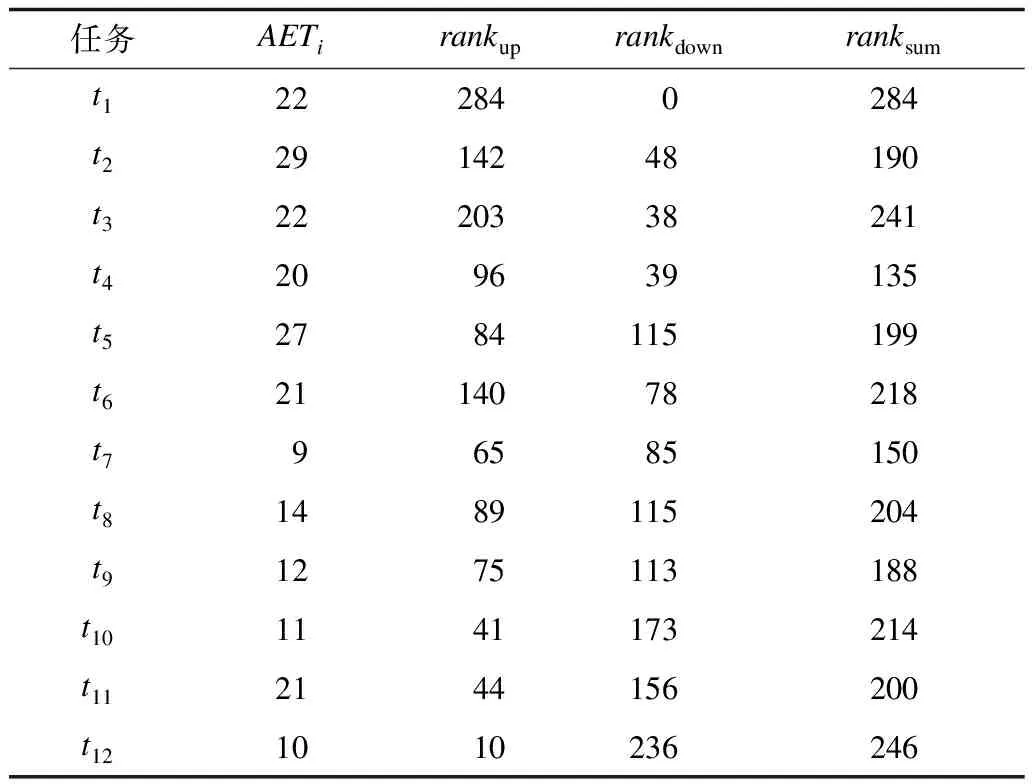
表3 各任务计算时间、改进升降秩及其和

表4 通过改进升降秩得到的CP与CCP

3.2 任务分配

任务分配阶段旨在寻找最佳资源执行CCP上的任务集。同时,为了避免增加通信代价,WS-DCCP算法规定一条约束关键路径上的所有任务均执行于同一资源。任务分配的优化目标是在满足约束关键路径子期限的情况下最小化工作流执行代价。

令ECT(CCPi,pj)为当前约束关键路径CCPi在资源pj上的最早完成时间,在单个任务的情况下,其值由式(5)决定。分层的子期限估算与当前CCP在资源pj上的最早完成时间之差为:

其中,levelsub-deadline为分配至包含当前CCP中最后任务ti的分层的子期限。如果当前CCP的最早完成时间超过分层子期限,即:

则表明式(15)可能为负值。同时,令CostCCPi,pj表示在资源pj上执行当前CCP上所有任务时的代价。

算法2给出了寻找最佳目标资源的执行过程。该过程需要考虑以下3种情况:

情况1由于云资源使用是基于账单数量的付费模式,以Amazon EC2为例,使用时间未达到1 h均按1 h间隔付费,如果任务可执行于还剩余使用账单时间的资源上,其执行代价为0。因此,在分配资源时,算法优先选择还剩余空闲付费间隔的资源,即:算法的第1步是在确保CCP的最早完成时间不超过分层子期限的情况下,优先考虑无代价的资源执行CCP,然后,选择最早完成时间最小的资源(即最快资源)。

情况2如果无法找到满足情况1的资源,需要提供一个新资源,此时算法在资源集中搜索满足分层子期限约束并且最低价的资源进行分配。

情况3对于较严格的期限约束,可能存在无法找到满足任务所在分层子期限的资源(即式(15)恒为负值)。如果存在某个CCP满足该条件,并不一定表明无法满足全局期限约束,而仅仅表明会违背子期限约束。此时,算法选择最佳性能的可用资源。

算法2寻找最佳资源算法

输入关键路径与子期限

输出代价最小化的最优资源

1.procedureResourceSelection(CCPi)

2.F←find all resources that have zero cost for CCPi

3.M←find all resources that can meet sub-deadline for CCPi

4.if (F∩M)//情况1

5.SelectResource←minECT(F∩M)

6.else if(M) then//情况2

7.SelectResource←minCost(M)

8.else//情况3

9.SelectResource←minCost(all resources)

10.end if

11.end procedure

3.3 算法时间复杂度

考虑任务数量为n的工作流DAGG=(T,E),假设DAG为全连通,则有向边的最大数量为n(n-1)/2,处理所有任务及其依赖关系的时间复杂度为O(n2)。对于WS-DCCP算法的第一阶段,需要将所有n个就绪任务在p个可用资源上进行遍历,其时间复杂度为O(np),而选择所有工作流任务的时间复杂度为O(n2p)。对于WS-DCCP算法的第二阶段,由于前一阶段的所选任务需要在所有可用资源上进行计算,其时间复杂度为O(p)。因此为任务选择资源的时间复杂度为O(np)。另外,在计算关键路径时需要计算任务的升秩和降秩值,其时间复杂度为O(n2p)。综上,WS-DCCP算法的时间复杂度为O(n2+n2p+np+n2p)=O(n2p)。

4 仿真实验

本节对算法性能进行仿真评估,构建2种形式的WS-DCCP算法:基于式(8)、式(10)的标准升秩与降秩算法WS-DCCP(SR),基于式(12)、式(13)的改进升秩与降秩算法WS-DCCP(MR)。另外,源于优化机制的相似性,选择IC-PCP[16]和JIT[20]作为基准算法。WS-DCCP(MR)同样使用逐层方式寻找关键路径,即:首先选择第一分层所有任务中拥有最高秩值的任务,然后在第二分层被选任务的子任务中,选择拥有最高秩值的任务。重复该过程,直到达到最后分层,找到所有其他关键任务,即可得到第1条关键路径。第2条关键路径重新回到剔除第1条关键路径后的子DAG中重新寻找。

4.1 实验环境与参数

通过仿真平台CloudSim[21]构造一个云数据中心和6种资源类型,资源的详细参数参考Amazon EC2设置,如表5所示。资源间的平均带宽参数参考Amazon AWS设置为20 MB/s。EC2单元的计算能力以每秒百万浮点操作次数MFLOPS进行度量。在实际的云计算环境中进行资源分配时,由于诸如时延、操作系统执行、资源类型、数据中心地理位置和资源请求量等因素的存在,可能导致资源启动时存在时延,因此,为了满足实际情况需求,仿真实验中为资源设置97 s的启动时间。

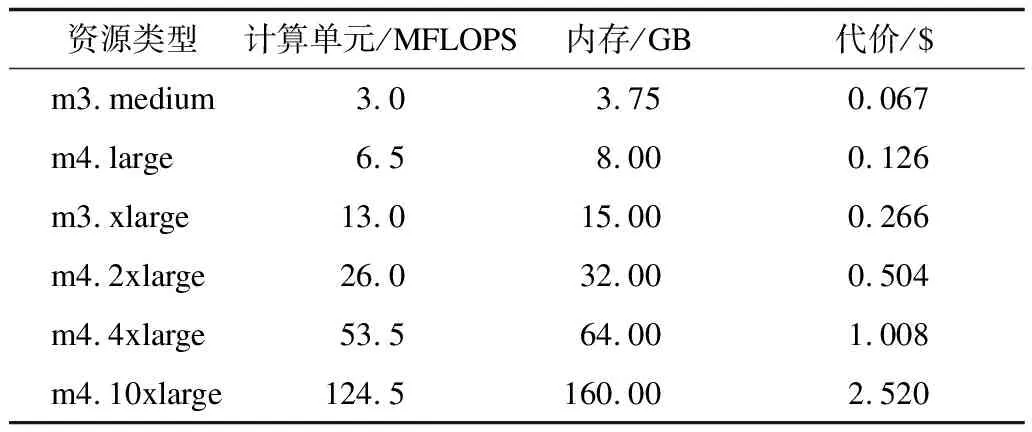
表5 资源参数

同时,为了评估算法处理真实负载的性能,实验中使用4种现实科学工作流进行测试,包括CyberShake、Montage、LIGO和SIPHT,利用Pegasus工作流产生器创建这4种合成工作流结构,同时将工作流规模设置为200个任务。

另外,为了评估算法的敏感性,实验设置不同的期限约束,其约束范围从较严格变化至较宽松。为了得到期限间隔,计算2种基准调度的长度:最快调度与最慢调度。

1)如果工作流的关键路径上的所有任务均执行于最快资源类型上,即可得到最快调度长度:

2)如果工作流的关键路径上的所有任务均执行于最慢资源类型上,即可得到最慢调度长度:

基于FS和SS,将工作流的期限定义为:

Duser=FS+α×(SS-FS)

(19)

其中,α表示期限因子,α∈[0.1,1],α以步长0.1进行递增,其值越小,期限约束越严格,其值越大,期限约束越宽松。

4.2 实验结果

为了比较算法的代价,引入满足期限的失效代价,即考虑任务执行失效对执行代价的影响。当执行结果无法满足期限约束时,视为一次失效。引入一个权重分配至算法返回的平均代价,令k表示满足期限约束的成功调度集合,则该权重代价可定义为:

在式(20)中,Cost(k)表示满足期限约束的代价(式(1)得到的最小值),SR表示算法的调度成功率,即满足调度期限的仿真实验次数与总的仿真运行次数的比率,定义为:

SR=n(k)/nTot

(21)

其中,nTot表示总仿真次数,nTot=50,n(k)为集合k的基数。将最低价调度考虑为所有任务均调度至最低价资源上执行,为了代价标准化处理,算法获得的权重代价为代价除以最低价调度。

图2显示了标准化代价的比较结果。可以看出,在多数情况下,WS-DCCP算法均拥有比IC-PCP更低的代价。在最严格期限约束下(α=0.1),IC-PCP算法在SIPHT和CyberShake 2种工作流中拥有较低的代价,但在Montage中代价较高,在LIGO中100%失效。同时,对于LIGO和Montage工作流,WS-DCCP算法在多数时间下能够以接近IC-PCP一半的代价调度工作流。此外,在所有工作流中,WS-DCCP(MR)算法在性能上优于WS-DCCP(SR)算法,除了CyberShake工作流的最严格期限约束的情况。总体而言,JIT算法降低通信代价的方式较IC-PCP可以降低一定代价,但由于其资源选择并非最优,因此在4种工作流中的代价均高于WS-DCCP算法。

图3显示了算法调度成功率的比较结果。可以看出,除了CyberShake工作流,WS-DCCP算法几乎可以成功满足所有期限约束。在最严格期限约束下(α=0.1),IC-PCP算法和JIT算法的调度成功率表现较差,其中,IC-PCP算法在LIGO工作流中几乎100%失效,而JIT算法的调度成功率略高于IC-PCP算法。结果还表明,WS-DCCP算法对于期限约束远没有IC-PCP算法和JIT算法表现得敏感,这反映WS-DCCP算法拥有比较稳定的性能。IC-PCP算法的不稳定性部分是由其较高的失效率导致的,源于该算法在选择资源分配时并没有做到最优选择。

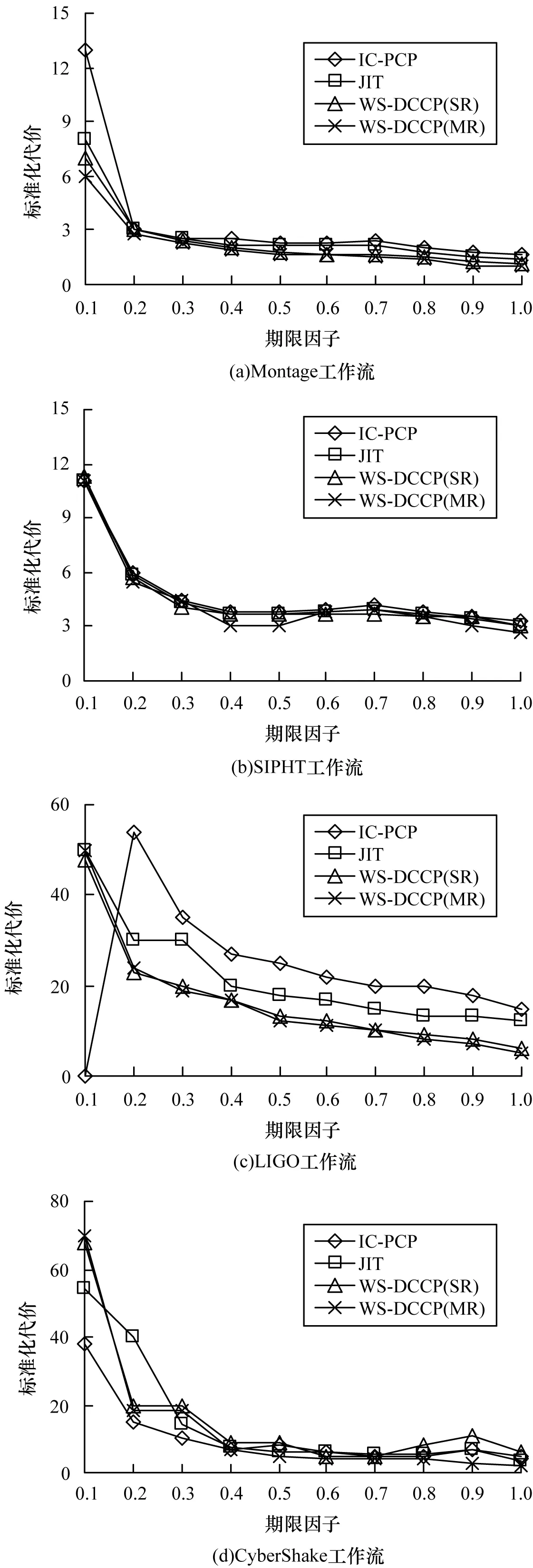
图2 算法代价比较

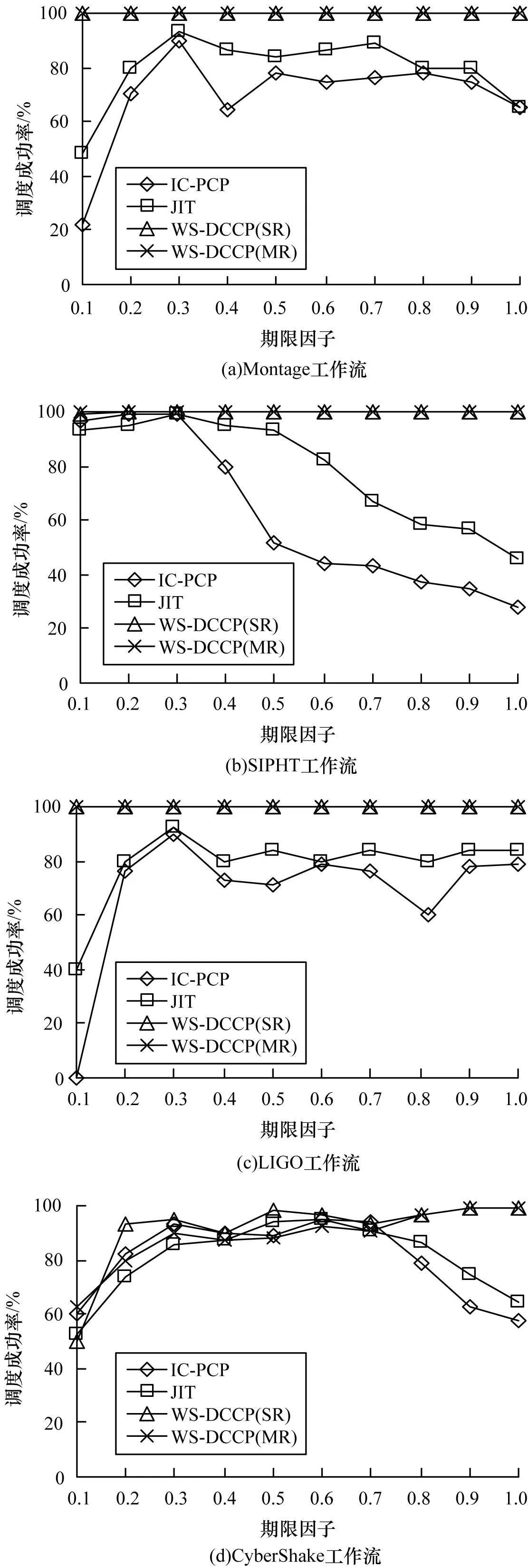
图3 算法调度成功率比较

总体来看,WS-DCCP算法虽然无法保证在所有工作流类型和所有程度的期限约束下达到工作流执行代价的最小,但可以在降低代价的情况下仍然拥有更高的调度成功率,其综合性能更好,性能也更稳定。

5 结束语

为实现期限约束下的执行代价最小化,本文提出一种基于关键路径的云工作流调度算法。通过求解工作流结构的约束关键路径,并将约束关键路径上的任务执行于同一资源上,降低资源间的通信代价。同时,设计基于改进任务升秩与降秩之和的约束关键路径求解方法,引入基于任务秩值与关键路径的机制,以降低工作流执行代价。实验结果表明,本文算法可以在满足期限约束的同时,降低工作流执行代价,提高调度成功率。下一步研究将集中于多约束条件下的关键路径求解,如将预算约束或资源能耗因素考虑在内,求解多目标的工作流调度优化。