新型箱—板组合浮式防波堤的水动力分析

何梦程，白兴兰

（1.浙江海洋大学港航与交通运输工程学院，浙江舟山 316022；2.浙江省近海海洋工程技术重点实验室，浙江舟山 316022;3.浙江海洋大学船舶与机电工程学院，浙江舟山 316022；）

近年来国内很学者提出了多种结构型式的浮式防波堤，并围绕其消浪情况、运动响应和锚泊安全开展了数值和模型试验研究。单方箱浮式防波堤由单个矩形方箱所构成，具有结构简单、修建方便、消浪效果明显等优点。如张伟等[1]利用AQWA软件，研究规则波与不规则波对浮式方箱防波堤的透射系数的影响，研究表明其透射系数随水深变化不大；邹志利等[2]研究了波浪对固定水面的浮式防波堤的非线性作用力的影响因素，包括不同吃水深度、波高、周期等。郑艳娜[3]利用数值模拟的方法研究浮箱的透射系数，并将结果与模型试验相比较，发现数值模拟的结果略大于模型试验。任慧龙等[4]对单模块方箱的锚链受力进行数值模拟研究，并分析了预张力和锚链拖地长度对浮体的影响，并得出了单模块方箱最优锚泊系统下预张力大小和锚链拖地长度。

多浮箱浮式防波堤由两个或多个方箱刚性连接，相对于单方箱浮式防波堤，可以间接增加防波堤的整体宽度，提高稳定性和消波性能。LIANG，et al[5]设计了一种双列并排多浮筒结构防波堤，并通过数值模拟和模型试验进行对比，得出该模型得具有较好的消浪效果。SYED，et al[6]研究多浮箱浮式防波堤的消浪性能，结果表明多浮箱浮式防波堤可显著提高消浪效果，且浮体的相对宽度、浮体吃水、浮箱间距以及锚固方式也影响其消浪性能。LEE，et al[7]就消浪性能、运动响应以及锚链受力等对单浮箱和双浮箱浮式防波堤进行研究对比。发现浮体的垂荡运动对消浪性能影响显著。肖霄等[8]对双浮筒-水平板浮式防波堤进行数值模拟，并计算分析了其锚链力以及运动响应，发现数值模拟结果与试验模拟结果有较高的吻合度。方箱-水平板浮式防波堤是在方箱底下安装固定水平板，起到增加浮体吃水，扰乱波浪运动，提高其稳定性的作用。王铁涛等[9]运用Ansys Workbench软件和图像后处理软件，研究双浮箱-双水平板浮式防波堤的消浪性能和运动响应特性，并设定不同影响因素：相对吃水深度、浮箱相对间距、相对板间距。但研究结果只涉及频域分析，并没有时域分析结果和锚链的受力情况。杨彪等[10]利用物理模型试验的方法，研究水平板层数、锚链刚度、浮体相对宽度和相对波高等对双浮箱-双水平板浮式防波堤的消浪性能、运动响应和两侧系泊力的影响，得出了相对宽度和锚链刚度是重要的影响因素，且水平板层数越多，防波堤整体性能越好。宋宪仓等[11]对5种不同结构形式的浮式防波堤的消浪性能进行数值模拟研究，发现这五种结构形式的防波堤其消浪性能差异明显，说明结构形式对消波效果具有显著影响，其中Y型浮堤结构消浪效果最佳，单方箱型的最差，而其他3种介于两者之间。陈智杰等[12]对方箱-水平板浮式防波堤进行水动力分析，研究其透射系数、运动响应和锚链受力情况，得出水平板层数是重要的影响因素之一。

基于上述研究成果，提出并设计了新型箱-板组合浮式防波堤，研究在不规则波作用下，运用AQWA对结构进行时域分析，讨论水平板与浮箱相对间距、水平板长度对结构运动响应、锚链受力和透射系数的影响。

1 基础理论

1.1 控制方程

在无旋运动的假设下，波浪运动为势波运动，及存在速度势函数φ，由下式定义：

在流体为不可压缩的均匀理想流体假设下，速度势的控制方程包括连续方程（拉普拉斯方程）和力平衡方程，可表示为：

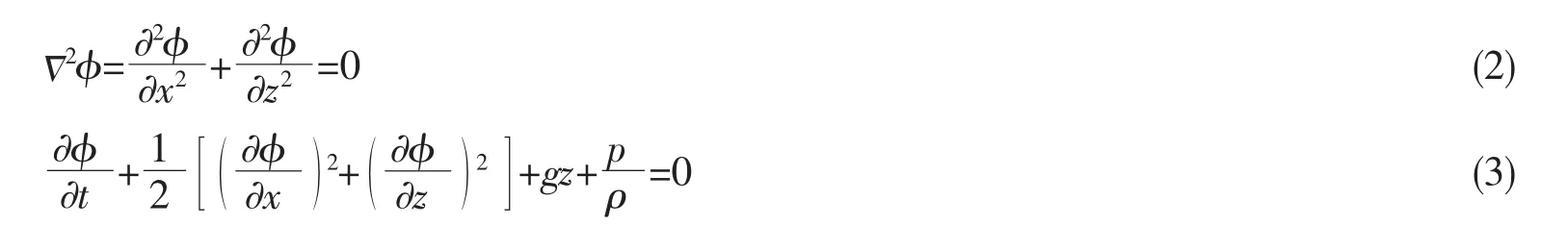
在海底处，水质点垂直速度为零，即

自由表面动力学边界条件

自由表面运动学边界条件：

将上式进行简化得到线性方程，并求其解为速度势函数的通解。

式中，φ为速度势；z为水面的法向矢量；ρ为海水密度；k为波数；c为波速；η为波面升高；d为水深。

方程（2）加边界条件（4）（5）（6）构成水波方程的定解问题，只需求得边值问题，则波场中的各运动要素便确定了。

1.2 锚链系泊力的计算

将锚链受力简化，得到：

竖向

水平方向

将式（8）和式（9）联立，并进行积分得到

式（11）即为锚链上任意一点的张力表达式。式中，θ为锚链与水平面的夹角；w为锚链在水中的单位长质量；T为锚链张力；Th张力水平向分力；s为锚链轴线长度方向；z为该点距离锚链底部的垂直距离。

1.3 透射系数的计算

防波堤的透射系数用Kt表示，为堤后波高和入射波高的比值，即

式中，Ht为堤后波高；Hi为入射波高。

2 防波堤数值模型

2.1 模型参数

建立新型箱-板组合浮式防波堤的模型，如图1、图2所示。两个浮箱通过刚性杆件连接，目的是增加浮体的整体宽度。浮箱底下连接双层水平板，目的是扰乱波浪水质点运动达到消浪目的，并且增加水平板可以间接增加浮体的吃水深度，增加浮体的迎浪面积。浮箱尺寸为：长12 m，宽6 m，高5 m；水平板尺寸为：长21 m，宽12 m，厚0.2 m；两浮箱间距为4 m，水平板间距为0.8 m，防波堤吃水5.9 m。

2.2 计算工况

数值模型模拟水深为30 m，有意波高为2 m，跨零周期为4 s；坐标原点为整个浮体的重心位置，锚链布置形式为对称平行布置，锚点为（80，4，30），系点为（5.5，4，5.9）（取绝对值）。

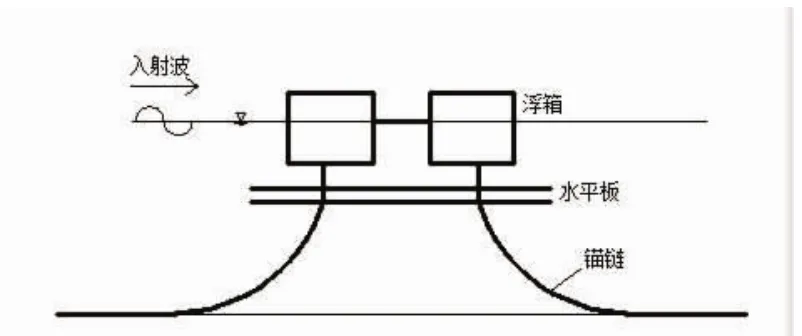
图1 箱-板组合浮式防波堤断面图Fig.1 The section view of the new composite pontoon-plate floating breakwater

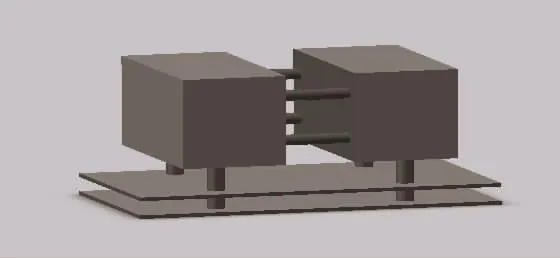
图2 箱-板组合浮式防波堤三维效果Fig.2 The 3D renderings of the new composite pontoon-plate floating breakwater

3 数值模拟验证

将本文的数值模型与文献[10]试验结果进行比较，对比结果如图3所示。横坐标B/L为结构宽度与波长的比值，纵坐标为纵摇运动位移幅值，从图3可以看出，三种不同结构的防波堤其纵摇变化趋势与试验结果基本吻合，且数值大小相差不大，表明了本文提出的新型箱-板浮式防波堤的可行性。其中模型A为双浮箱无水平板；模型B为双浮箱-单水平板；模型C为双浮箱-双水平板，即为本文模型。表1为数值模拟与试验研究纵摇对比数据。

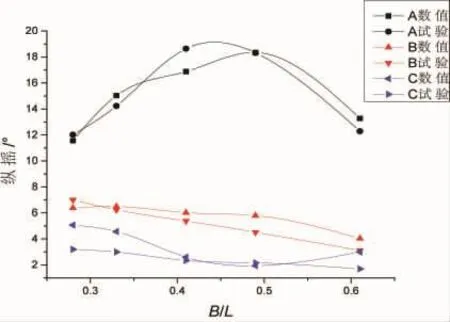
图3 箱-板组合浮式防波堤纵摇运动比较Fig.3 Pitch movement comparison of the new composite pontoon-plate floating breakwater

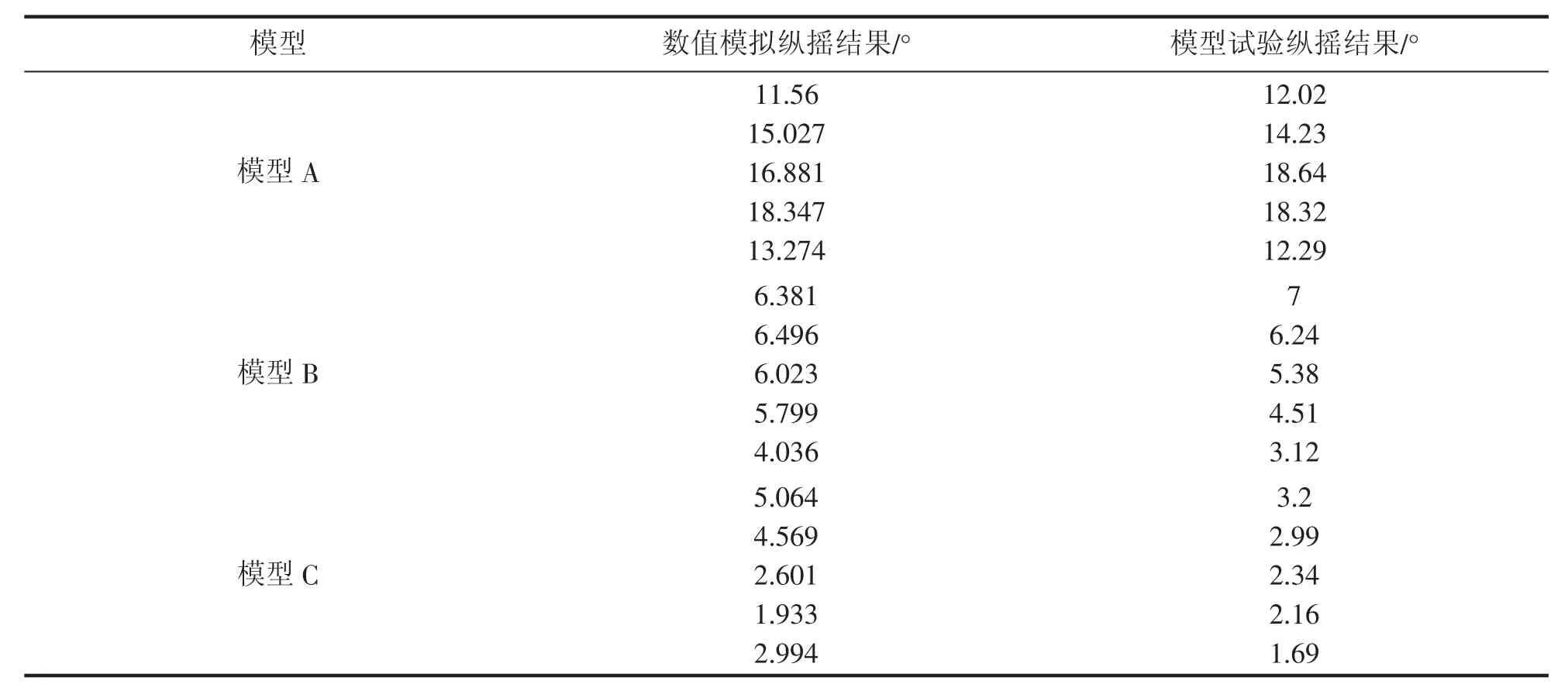
表1 数值模拟与试验研究纵摇比较列表Tab.1 Numerical simulation and experimental study pitch comparison list

海况条件为：波浪为P-M波谱，有效波高为2 m，周期4 s，为单方向不规则波，通过数值模拟计算得到结构横荡、垂荡和纵摇的位移相应曲线，如图4所示，模型受不规则波作用下，其运动响应存在一定的非线性，运动规律并不明显。

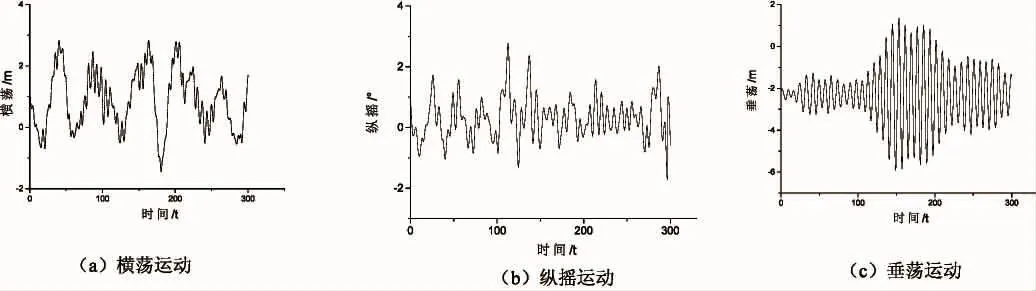
图4 防波堤运动响应时历曲线Fig.4 Break water movement response time curve

4 结果分析

4.1 水平板与浮箱的相对间距对结构的影响

通过改变双水平板与浮箱的相对间距，保持双水平板间距不变，研究结构运动响应、锚链受力和透射系数Kt变化情况。双水平板与浮箱的间距d分别取1.3 m、1.7 m和2.1 m。

4.1.1 防波堤运动响应和锚链系泊力

通过数值计算，得到了结构的运动响应和锚链系泊力，如图5、图6所示。其中横坐标为B/L，表示相对宽度，即模型的整体宽度与波浪波长的比值。纵坐标分别为各运动幅值和锚链系泊力。从图5可以看出：随着相对间距d的增加，模型横荡、垂荡和纵摇位移幅值都因此减小，因为随着d的增加，结构的吃水较大，惯性力增大，运动响应减小。因此，可以通过安装水平板来调整浮体的吃水深度，以相对较低的经济成本达到较好的防护效果。从横荡运动的位移幅值变化曲线可以看出，当B/L=0.6左右时，其位移幅值达到最小。垂荡和纵摇的运动变化规律基本一致，当相对宽度B/L<0.7时，两者都随着相对宽度B/L的增加而显著减小；当B/L>0.7时，继续增加相对宽度，纵摇和垂荡幅值的变化趋于平缓。因此，当B/L为0.6～0.7之间时，浮体整体的运动响应达到最小值。

从图6可以看出，反映了两侧锚链系泊力随相对宽度B/L和相对间距d的变化曲线，随着B/L的逐渐增大，迎浪侧系泊力也随之增大，且当B/L为0.8时达到最大值，随后又有减小趋势。相对间距d对迎浪侧系泊力影响显著，d越大，锚链受力越小，这与浮体的运动响应规律相符合，运动响应越大，迎浪侧系泊力也越大。由于波浪的直接作用，迎浪侧系泊力始终大于背浪面，因此背浪侧锚链经常处于松弛状态，且无明显变化规律，但当相对宽度B/L>0.7时，背浪侧系泊力逐渐减小，这是因为该浮体受短周期波浪作用，基本处于被推压状态，此时背浪侧系泊力随波浪波长的减小而逐渐减小。

加强中药挥发油提取设备的研发，使其逐步转型升级，实现中药挥发油提取过程中可在线监控。自动化与智能化提取设备不仅可取代传统依赖人力制造的生产方式，降低工人劳动程度和人工操作比例，还可减少提取过程中的污染及人为的不确定因素，使中药挥发油质量得以提升，同时提高生产效率、节约成本[26]。

图5 防波堤运动响应随相对宽度B/L的变化曲线Fig.5 Variation curves of motion response of breakwater with relative width B/L

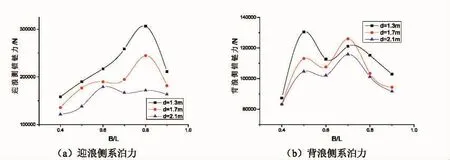
图6 防波堤锚链系泊力随相对宽度B/L的变化曲线Fig.6 Variation curves of mooring force of breakwater anchor chain with relative width B/L

4.1.2 水平板与浮箱的相对间距d对透射系数的影响

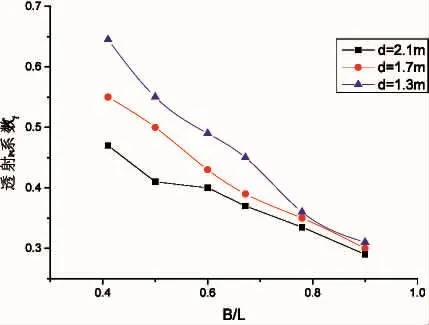
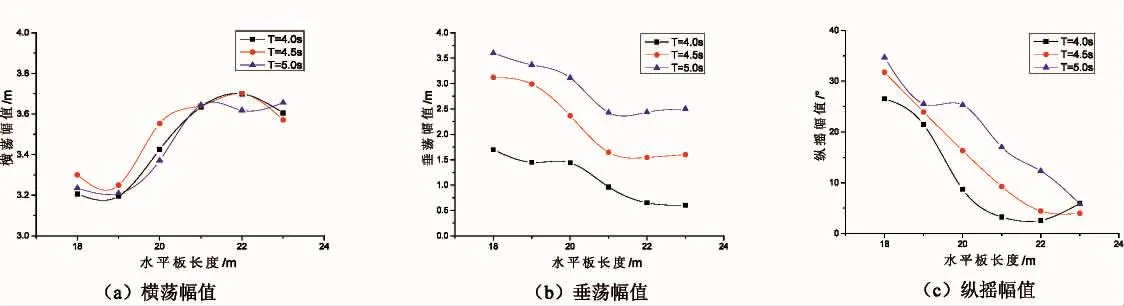
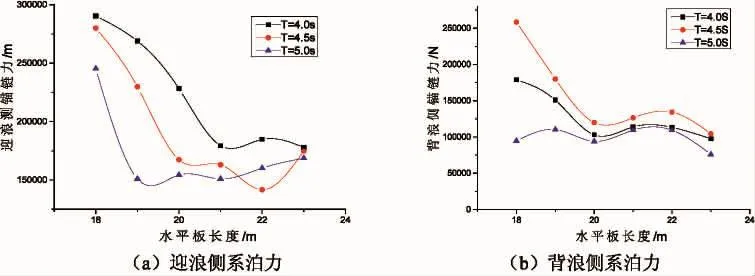
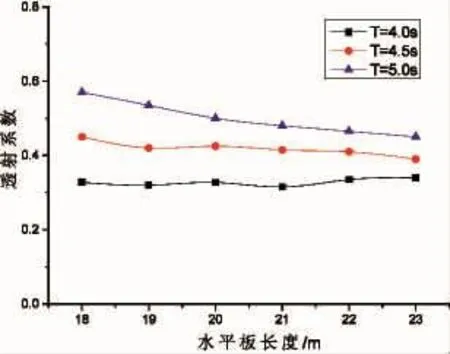
将ANSYS-AQWA计算的结果导入经典AQWA的图像后处理软件中，求解计算浮式防波堤的透射系数。透射系数的求解关键在于堤后波高的确定，本文采取平均值法求解堤后波高。先确定堤后波高的矩形范围，取-6 m

从图7可以看出，防波堤透射系数Kt随B/L的变化曲线，B/L越大，Kt越小，表明Kt与浮体吃水深度有直接关系，即吃水越大，结构对波浪的阻挡面积越大，导致透射波高减小；相对宽度越大，Kt越小。而随着相对宽度逐渐变大，水平板与浮箱的相对间距对Kt的影响越来越小，这是因为短周期波浪的能量主要集中在水面附近。因此在面对长周期波浪的情况下，增加浮体吃水深度可以有效减小Kt。

4.2 水平板长度对结构的影响

为了研究水平板的长度对结构运动响应、系泊力和Kt的影响，将水平长度设置为 18、19、20、21、22、23 m，波浪周期为 4、4.5、5 s，计算结果如图 8～10 所示。

4.2.1 水平板长度对结构运动响应和系泊力的影响

从图8可以看出，随水平板长度的增加，横荡运动的位移幅值先增大再趋于平缓，而垂荡和纵摇运动的位移幅值都随相对宽度的增加而逐渐减小。横荡运动与波浪周期没有显著关系，对垂荡和纵摇运动而言，波浪周期越大，位移幅值显著增加。计算表明：水平板长度为21 m左右时，结构的综合运动响应较小，达到最佳状态。

图7 防波堤透射系数随相对间距B/L的变化曲线Fig.7 Variation curves of transmission coefficient of breakwater with relative spacing B/L

图8 不同波浪周期下防波堤运动响应随水平板长度的变化曲线Fig.8 Variation of motion response of breakwater with horizontal plate length under different wave cycles

图9 不同波浪周期下防波堤系泊力随水平板长度的变化曲线Fig.9 Variation of the mooring force of the breakwater with the length of the horizontal plate under different wave cycles

4.2.2 水平板长度对防波堤透射系数Kt的影响

从图10可以看出，给出了不同波浪周期下的Kt随水平板长度的变化曲线。由图可知，Kt随着波浪周期的增加而增大，这是因为长周期波浪作用时，浮体的位移幅值明显大于短周期波浪情况，产生更强烈的辐射波，导致堤后波高较大。当周期T=4.0 s时，水平板长度对Kt基本不产生影响，基本保持在0.32左右。周期越大，水平板长度对透射系数影响越大，当周期T=5.0 s时，Kt随水平板长度的增加而减小，且变化幅度逐渐变缓。这与浮体的垂荡变化基本一致，表明垂荡运动对Kt有一定影响。

图10 Kt随水平板长度的变化曲线Fig.10 Ktchanges with the length of the horizontal plate

5 结语

本文对新型箱-板组合浮式防波堤进行了水动力分析，研究其在时域情况下，不同影响因素对结构运动响应、系泊力以及波浪透射系数Kt的影响，包括水平板与浮箱相对间距、水平板长度和相对宽度等，为防波堤结构的优化设计提供重要参考，本结构模型能够在保持稳定的状态下提高消浪性能。具体如下：

（1）水平板与浮箱的相对间距d对结构运动响应、系泊力和Kt有显著影响作用。d的变化使得结构的吃水深度和惯性力发生变化，同时结构的固有频率也会发生改变，计算结果表明：位移幅值、系泊力和Kt随d增大而减小，但当B/L>0.5时，变化不明显。

（2）该浮体可以有效抵御短周期波浪的侵袭，而在应对长周期波浪时消浪效果不佳。

（3）水平板长度对新型箱-板组合浮式防波堤运动响应以及系泊力具有显著影响，而对透射系数的影响受波浪周期的制约。计算表明：水平板的长度主要对运动响应和系泊力影响较大，可以通过水平板来改进浮体的水动力响应和系泊稳定性，就本模型而言，当水平板为21 m时，运动响应和系泊力达到最理想状态。