基于隐高斯模型的多元离散数据异常检测

李楠芳 王 旭 邵 巍 马学智 张菊玲 梁 涛*

1(国网青海省电力公司电力科学研究院 青海 西宁 810008)2(国网青海省电力公司 青海 西宁 810008)3(国网青海省电力公司信息通信公司 青海 西宁 810008)4(电子科技大学计算机科学与工程学院 四川 成都 610000)

0 引 言

异常检测[1]是数据挖掘领域中的一项非常重要的技术，它通过对数据特性的分析，找出与事先定义的正常模式不相符的异常模式，并通过分析异常模式特性来解决应用领域的异常事件。异常检测在网页恶意攻击[2]、医疗疾病检测[3]、信用卡诈骗、机器异常检测、垃圾邮件识别等任务中处于重要地位。根据数据是否有可用的标签，可将异常检测大致分为3类：有监督异常检测、半监督异常检测[4]和无监督异常检测。

在本文中，我们主要针对的是半监督的异常检测，即所采用的训练数据仅仅包含正常模式类别数据，并基于此类数据建立相应的表现正常模式类别行为的模型，最后用建立好的模型去识别测试数据中的异常模式数据。

对于半监督异常检测常用的方法是基于分布的方法，即只对正常模式数据或异常模式数据的分布建模，捕获正常(异常)模式数据行为的概率分布，进而将低概率的数据视为异常。在本文中我们采用对于正常模式数据建模。在已知的学习正常模式的方法中，既有参数法也有非参法。对于连续数据的异常检测，常常使用高斯分布，混合高斯分布以及基于核函数的方法等。而对于离散数据，常常采用的是多项式分布，狄利克雷多项式分布等。本文中，我们主要针对于离散数据建模。

但是在处理小规模多元离散数据集的时候，上述的模型会面临维数灾难的问题[5]，并且很难检测出异常模式行为，因为我们不得不处理这样的困境：离散数据的可能取值数量与该数据所包含的属性数量成指数增长，且可得到的小规模多元离散数据集中仅仅包含离散数据可能性取值的一小部分。所以我们要建立一个基于分布的模型，类似于深度置信网络(DBN)[6]和变分自编码器(VAE)[7]等深度生成网络，但是DBN和VAE都是深层网络，进而参数数量非常大，并且对于数据量的依赖很大，在处理小规模数据的时候特别容易过拟合。

在本文中，我们采用隐高斯模型(LGM)[8]来处理小规模多元离散数据的异常检测，用LGM对正常的数据建模，从而获得正常数据的概率分布模型。LGM是一种隐变量模型，它假设多元离散数据是通过低维连续空间的线性映射生成，它通过将线性映射的参数贝叶斯化，以减少模型在小规模样本集下产生过拟合现象的风险，从而有效地将异常模式行为检测出来。试验结果表明，在小规模离散数据集上LGM相比于其他的异常检测技术能够更好地检测出异常数据。

1 LGM模型简介

在隐高斯模型(LGM)中，我们假设有N个数据样本Y=[y1,y2,…,yN]，第n个数据样本用向量yn表示，相应的在隐空间中对应N个隐空间数据X=[x1,x2,…,xN]，第n个数据用向量xn表示，同时假设yn为D维向量，xn为L维向量，且D大于L。对于yn中的每个属性用ydn表示，ydn可从一个有限的离散集[0,1,…,Kd]中取值。隐变量xn服从一个均值为μ方差为Σ的高斯分布，如式(1)所示，其中θ={μ,Σ}。每个分类变量ydn以线性映射wdn的形式被参数化，如式(2)和(3)所示。

(1)

γdn=Wdxn+B0d

(2)

(3)

式中：Wd∈(K+1)×L是因子权重矩阵，B0d∈K+1是偏移向量，且γdn∈K+1，式(3)中的似然是在数据ydn上所有维度D上的分解。

2 基于LGM的异常检测

我们假设训练数据有N个，用Y=[y1,y2,…,yN]表示，其中yn∈D,ydn表示yn中第d个属性值，ydn取值范围为0,…,Kd，隐变量空间中对应于训练数据Y的数据用X=[x1,x2,…,xN]表示，其中xn∈L。

我们要对训练数据建立对应的概率分布，如下所示：

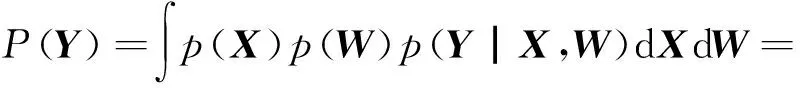
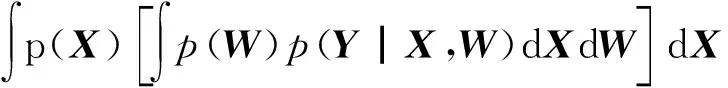
(4)

(5)

进而可以将W积分出来，得到p(Y|X,β)，如公式所示：

(6)

式中：Y:,d表示Y的第d列，进而可得公式：

p(Y:,d|X,β)=N(Y:,d|0,XXT+β-1I)

(7)

可以看到XXT+β-1I是线性的，式(7)等价于一个具有线性核的高斯过程，为了对高斯过程进行高效的推断，我们考虑在推断过程中引入伪输入T∈M×D×K[9-10]，进而式(4)可写成式(8)：

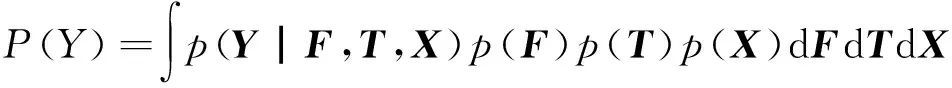
(8)

那么基于文献[11]和式(8)可得到未观测变量的后验P(F,T,X|Y)，该式可通过变分分解近似估计为：

q(X,T,F)=q(X)q(T)p(F|X,T)

(9)

式(9)中q(X)和q(T)可以从式(10)中得到：

(10)

式中：udk、Σd、φml、及ξml都是变分参数，再根据杰森不等式，logp(Y)可以用式(11)得到：

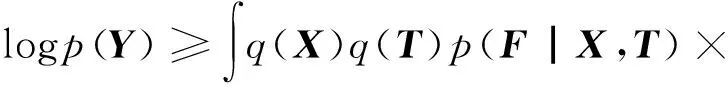
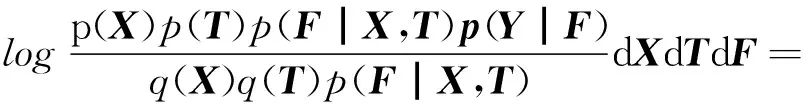
-KL(q(X)‖p(X))-KL(q(T)‖p(T))+

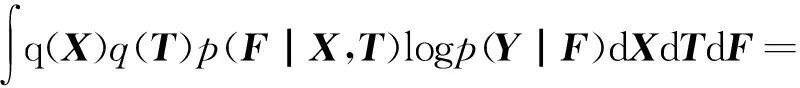
Ψ

为了精确地得到p(Y)，我们要做的就是最大化Ψ，因为Ψ是其下界。

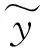
(12)

进而可式(13)：

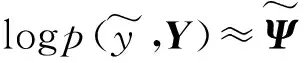
(13)

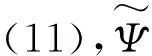
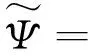
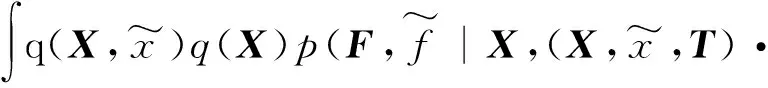
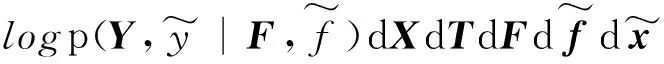
(14)

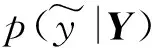
(15)

至此，我们可以利用式(15)对于测试集中的数据进行测试，从而得到模型的最终表现结果。

3 试验结果

为了评估我们所提出的模型的表现效果，特进行分类试验。我们所采用的数据来自UCI机器学习库。

在本试验中，将用我们提出的方法和另两种方法(基于朴素贝叶斯的多项式方法(NB-M)；基于朴素贝叶斯的狄利克雷方法(NB-DCM))做比较，这两种方法对于小规模分类数据集的概率分布建模效果良好。

首先，我们分别用NB-M、NB-DCM以及LGM方法对只包含正常行为模式的概率分布进行建模；然后，我们用一个测试集模拟异常检测的场景，即在测试集中包括正常行为数据和异常行为数据，但是异常行为数据的数量要远小于正常行为数据的数量，这样便能够基本模拟出日常所遇见的异常检测场景；最后我们用之前多学习到3种概率分布模型分别在测试集上进行异常检测试验，比较这3种方法的优劣。

为了增加说服力，我们在进行挑选用于建模的训练数据的时候，随机挑选5次，每次用于建模的数据是各不一样的，但是每次挑选的数据数量是一样的，然后用这5次训练出来的模型对测试集进行测试，最后取平均值作为该模型最终的表现能力。

在比较各个模型的检测能力的时候，我们采用如下方法：使用top-k异常分数评估包含在测试数据中的异常数据数量。此外，我们也做出每个检测模型的ROC曲线以及计算出ROC曲线所对应的AUC面积。

3.1 毒蘑菇检测

毒蘑菇数据集中，每一表示蘑菇的数据包含22个特征，包含蘑菇的帽、鳃、茎，面纱等特征，这22个特征决定了该蘑菇是否是可食用的蘑菇。显然可食用的蘑菇就是所说的正常行为模式，而那些毒蘑菇就是异常行为模式。我们的目标就是在一堆既包含可食用蘑菇又包含毒蘑菇的数据中，检测出代表毒蘑菇的数据。

为了表现模型在小规模数据集上能力，我们仅仅随机抽取300个可食用蘑菇数据作为模型的训练集，随机抽取3 600个可食用蘑菇数据和400个毒蘑菇数据作为模型的测试集。

表1向我们展示NB-M、NB-DCM及LGM模型5次预测的结果，结果以ROC曲线下的AUC面积给出，总面积为1，AUC面积越大表示模型所表现的效果越好。通过对比这三种模型的5次检测结果，发现我们的模型总体上明显优于NB-DCM模型和NB-M模型，对比NB-M的优势要更加明显，具体结果如表1所示。

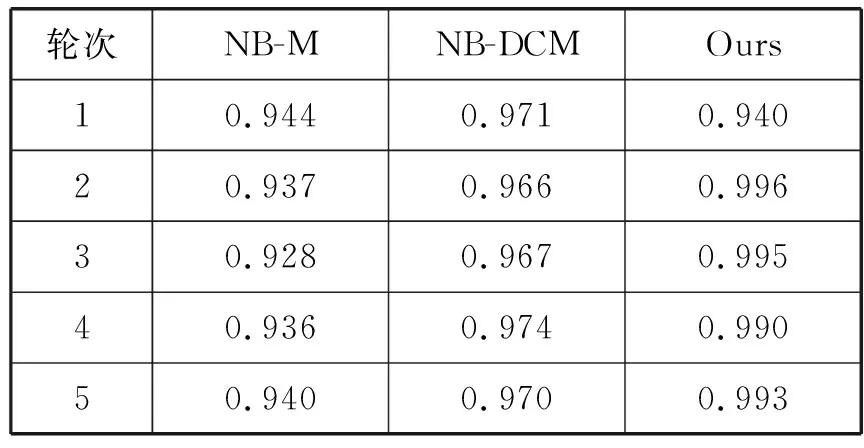
表1 毒蘑菇检测结果(AUC面积)

相应的，我们也做出NB-M、NB-DCM以及我们的模型所对应的平均ROC曲线和AUC面积，如图1所示。其中粗实线表示我们模型的ROC曲线和对应ROC面积，细虚线表示NB-DCM模型的ROC曲线和对应的AUC面积，细实线表示NB-M模型的ROC曲线和对应的AUC面积。从图1中可以明显看到我们所提出的模型要优于NB-M模型和NB-DCM模型。

图1 毒蘑菇检测结果ROC曲线和AUC面积

3.2 心脏病检测

心脏病数据集中包含的是心脏病病人和健康人心脏的SPECT图，每一个数据样本描述一个人的心脏状况，包含22个特征。在我们的试验里，我们将健康人的心脏数据当作正常行为模式，而将心脏病患者的心脏数据作为异常行为模式。显然我们的目的就是在一堆包含健康人心脏数据和心脏病患者的心脏数据中检测出心脏病患者的数据。

这里我们为了进一步验证模型在小数据集上表现能力，特地在更小的数据集合上进行试验。仅仅随机抽取20个数据作为模型的训练集，同时随机抽取35个健康人数据和4个心脏病患者数据作为模型的测试集。

在心脏病检测试验中我们同样对NB-DCM模型、NB-M模型以及我们所提出的模型进行5次对比试验，得出的结果如表2所示。表2展示了用5次随机挑选的健康人数据分别基于NB-M、NB-DCM、我们的方法各建立5个模型，再用基于每种方法的5个模型分别对包含健康和心脏病患者的测试集进行检测，根据最后的检测结果计算得到相对应的AUC面积，AUC总面积为1。从表2结果来看，我们的模型明显要优于NB-M和NB-DCM模型的结果。

表2 心脏病检测结果(AUC面积)

相应的，我们也做出NB-M、NB-DCM以及我们的模型所对应的平均ROC曲线和AUC面积，如图2所示。其中粗实线表示我们的模型的ROC曲线和对应ROC面积，细虚线表示NB-DCM模型的ROC曲线和对应的AUC面积，细实线表示NB-M模型的ROC曲线和对应的AUC面积。从图2中可以明显看到我们所提出的模型要优于NB-M模型和NB-DCM模型。

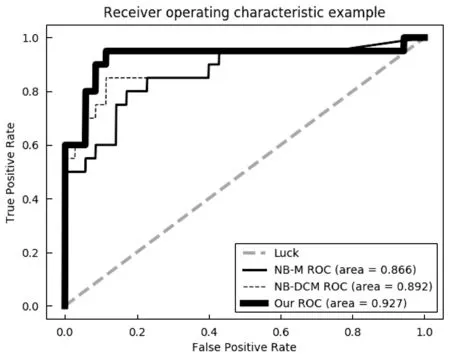
图2 心脏病检测结果ROC曲线和AUC面积

4 结 语

我们提出了一种基于半监督学习的异常检测方法。我们的主要思路是基于LGM对正常行为模式的概率分布进行建模，提取出正常行为模式的特性，进而检测出异常行为模式。并且由于高斯过程的非参贝叶斯特性，LGM可以很好地捕获正常行为模式的概率分布，即使是包含正常行为模式的小规模数据集合。同时试验结果也表明了我们的异常检测的方法相对于其他的异常检测方法在小规模多元离散分类数据上是很有效的。