前推回代法在故障配电网中的收敛性分析及改进算法

梁梦可，滕欢，李雪松，吴泽穹

(四川大学 电气信息学院,成都 610065)

0 引 言

配电网潮流计算是配电网经济安全运行分析、网络重构和故障处理的基础，而与输电网络相比，具有自己独特的特点，配电网往往呈现出辐射状结构(闭环设计)、存在较多分支和高阻抗比等特点。在进行配电网潮流计算时，雅克比矩阵会呈现奇异特征，导致传统的PQ分解法和牛顿拉夫逊法会出现收敛困难，计算缓慢，效率不高等特点。

传统的前推回代潮流算法，对于辐射状和高阻抗比的配电网具有良好的适应性，其具有计算原理简单，收敛性好，精确度高等特点，使得其在配电网潮流计算中得到了广泛应用[1-2]。文献[3-5]针对前推回代潮流算法进行了一定改进措施，提高了其潮流运算速度；文献[6]考虑了负荷的电压静态特性，完善了其实际应用性。随着分布式电源的发展，传统配电网网络从单一电源转化为包含各种新能源的多电源网络；文献[7-8]分别从新能源接入配电网的角度进行了考虑，分别对传统的前推回代算法进行了一定改进。

针对故障配电网的潮流计算却少有研究和考虑，文献[9]将前推回代潮流算法应用到了配电网故障定位中，但是忽略了故障点将改变配电网的收敛特性，使得传统的前推回代潮流算法呈现发散状态。针对配电网故障潮流不收敛的现象，分析了故障点导致前推回代潮流算法难以收敛的原因，通过添加松弛因子，对传统的前推回代潮流算法进行改进，改善了潮流计算的收敛性，并保证了潮流运算结果的准确性。该方法通过在迭代向量之间添加松弛因子，对新的迭代向量进行约束，减小了不动点迭代矩阵的谱半径，使之满足压缩映射的条件，从而保证潮流计算的收敛性[10]。通过在MATLAB上进行算例仿真，验证了该方法的有效性和准确性。

1 前推后代潮流算法原理

在实际应用中，大规模科学与工程计算产生的方程系数往往是大型稀疏矩阵，此类方程的求解往往采用迭代法。前推回代潮流算法本质也是通过迭代算法求解线性代数方程组，因此会面临收敛性问题[11]。

1.1 迭代方程的原理分析

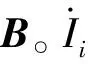
(1)

V是结点电压向量，为：

(2)

设x(0)是初始迭代向量，则Jacobi迭代算法的迭代矩阵可表示为：

xk+1=Bxk+g

(3)

式中迭代向量x=[INV]T；g是常数向量。

根据分析可知，基于前推回代的潮流算法采用的Guass迭代法。在Jacobi算法基础上进行了改进，其迭代矩阵B可分解为：

B=L+U

(4)

式中L是矩阵B的严格下三角矩阵；U是矩阵B的严格上三角矩阵。

Guass迭代法的分量形式为：

(5)

其矩阵形式为：

xk+1=Lxk+1+Uxk+g

(6)

通过对式(6)进行变形，构造的迭代方程为：

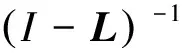
(7)

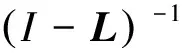
ρ((I-L)-1U)<1

(8)

对于正常运行的配电网，前推回代潮流算法能够取得良好的收敛性；但是，针对故障配电网，故障点将改变迭代矩阵的收敛性，甚至趋于发散状态。文章在式(5)的基础上，通过添加松弛因子改变其收敛性，其分量形式为：

(9)

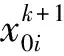
迭代方程的矩阵形式为：

xk+1=(1-ω)xk+ω(Lxk+1+Uxk+g)

(10)

对其进行变形，即：

(11)

式中ξ是Guass法的迭代矩阵，根据ξ的谱半径可以确定迭代方程是否收敛。当ξ的谱半径小于1，迭代方程处于收敛状态，即：

ρ(ξ)<1

(12)

1.2 迭代矩阵B和常数向量g

配电网呈现辐射状特点，采用结点分层来描述网络结构，其原始数据记录如下格式：

支路参数矩阵BranchM:

{父节点子节点支路阻抗参数}

任一条支路的子节点具有唯一性，则阻抗ZLj可表示子节点是j的支路，即:

结点参数矩阵NodeM:

{结点号有功功率无功功率}

在配电网潮流计算中，负荷的模型的选取直接影响算法的收敛性，在短路计算中，负荷模型通常选取恒定阻抗模型。假定在故障前后，负荷的阻抗恒定不变，通过故障前的功率数据计算出负载阻抗ZLD，即：

(13)

式中PLD和QLD是故障前的负载有功和无功功率；VLD是故障前的负载电压[12]。

根据配电网的支路参数矩阵中节点关系，可求得此种关系运行方式下的结点关联矩阵AT，矩阵AT可表示整个配电网结构[13]。

(14)

式中n表示节点总数；aij表示节点i与结点j的关系，只有当结点i是父节点，子节点是结点j时，aij=1；否则，aij=0。

针对迭代矩阵B收敛性分析,需要对其进行参数求解，根据公式，配电网的线性方程为：

(15)

式中n-1阶方阵Bn是迭代矩阵B的分块矩阵；n-1阶向量gn是常向量g的子向量；根据配电网结点关联关系，本文将分别对Bn和gn进行求解。

根据算法原理可知结点负载电流只有结点电压有关，则B1和g1是零矩阵，B2是对角阵；其可表示为：

(16)

即：

(17)

根据基尔霍夫定理，忽略线路对地导纳情况下，线路电流Iij等于结点j的负载电流和所有下游结点负载电流之和，根据关系矩阵AT可求得矩阵ATH，为：

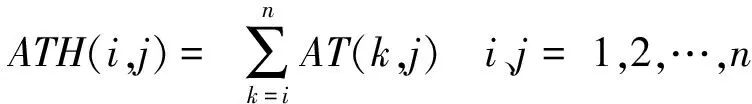
(18)

式中i，j表示ATH(i，j)在矩阵ATH位置，假定ATH(i，j)=1，则表示结点j是结点i的下游结点。令ATH的对角元素为1，即：

ATH(i,i)=1i=1,2,…,n

(19)

则流经支路Lij电流为：

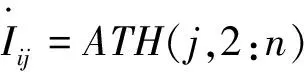
(20)

式中向量ATH(j,2:n)是矩阵ATH的j行、2到n列的元素。

同理ATO是AT的转置矩阵，可以表示子节点与其对应的父节点的关系，例如矩阵ATO中存在aij=1，则表示节点j的父节点是结点i，其结点i的电压为：

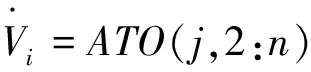
(21)

对于任一条支路，其子节点与父节点的电压关系为：

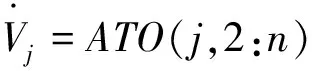
(22)

根据式(22)，可得：

(23)

B4=AOT(2:n,2:n)

结点2的电压跟根节点电压有关，即：

(24)

可知：

(25)

式中向量g2中其他元素为零。

通过对潮流计算原理以及迭代矩阵B收敛性分析，当配电网发生对地故障时，故障点将改变最初建立的迭代矩阵B，根据式(8)可知，进而影响迭代算法的收敛性。当迭代方程的谱半径大于1时，算法的收敛性将会被破坏，进而导致不收敛现象的发生，通过添加松弛因子能够使得遭到破坏的迭代矩阵重新收敛，将在第三章进行算例分析和验证。

2 改进前推回代潮流算法

配电网往往呈现辐射状结构，前推后代法是配电网潮流计算中广泛采用的一种方法。改进前推回代潮流计算过程如下：

(2)从第一层的末梢负荷结点开始，根据负载阻抗，由k次迭代的结点电压可计算流入该节点j的负载电流，为：

(26)

式中j是最末稍结点的负荷节点号；i是所在线路区段末结点的父节点号。

(3)从第二层(非末梢结点)开始逐层计算支路电流，根据基尔霍夫定理可求得：

(27)

式中j为是支路子节点号；i是该节点的父节点。

(4)由步骤(2)和步骤(3)可求得所有支路的电流，再根据已知的根节点电压，由根节点向后依次求得各个负荷结点的电压，为：

(28)

(29)

(4)计算各个负荷节点的电压幅值修正值。

(30)

(5)计算结点电压修正量的最大值max(ΔUj)；

(6)判断收敛条件

max(ΔUj)<ε

(31)

式中若最大电压修正量小于阈值，则跳出循环，输出结点电压值和负载电流；否则重复以上步骤，直至满足收敛条件。迭代结束后，输出结点电压和负载电流。

3 算例分析

以IEEE33结点标准模型进行算例分析，其结构及结点编号如图1所示。

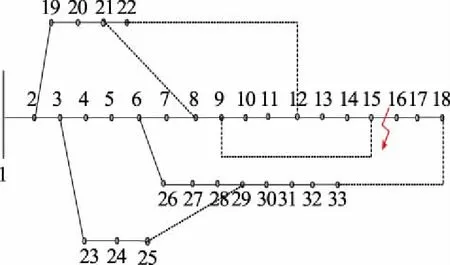
图1 IEEE 33结点标准模型Fig.1 Model of the IEEE 33-node test feeder

假定在结点15和16中间位置发生对地故障，故障电阻是5 Ω。利用Guass迭代法的前推回代潮流算法进行计算，仿真结果证明配电网在故障状态下，此算法不能处于收敛状态，最终求得的结点电压和负荷电流趋于无穷大。对迭代矩阵进行收敛性分析，求得其谱半径为：

ρ((I-L)-1U)=1.303

(32)

因此，前推回代算法的迭代方程不满足收敛状态，验证了仿真结果。

对改进的潮流算法进行仿真分析，当松弛因子ω=0.5时，其谱半径为：

ρ(ξ)=0.831

(33)

改进的潮流算法通过松弛因子改变了迭代方程的谱半径，使之满足压缩映射的条件，从而保证潮流计算的收敛性。

为了进一步对两种算法进行对比，选取故障点为分析结点，分析其电压幅值和迭代次数的关系。改进前的算法，其结果如图2所示；改进后的算法，其结果如图3所示。

分析可知：改进前的算法在故障情况下不具有收敛性，结点电压随着迭代次数增加趋于无穷，并且在前20次迭代过程中，由于新的迭代电压不受前次结点电压的约束，整个迭代过程呈现振荡递增；对比可知改进的算法能够保持较好的收敛性，迭代过程呈现振荡衰减，并且逐渐趋于稳定值，证明了松弛因子ω能够对结点电压进行约束，使得迭代过程从发散状态转化为收敛状态。

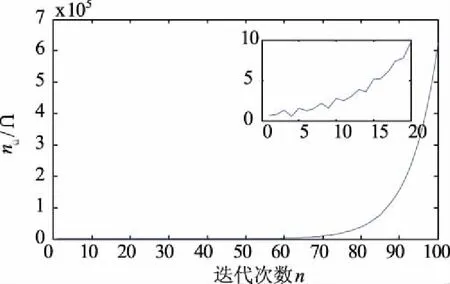
图2 前推回代法电压与迭代次数关系Fig.2 Relation between voltage and iteration times under forward/backward sweep substitution

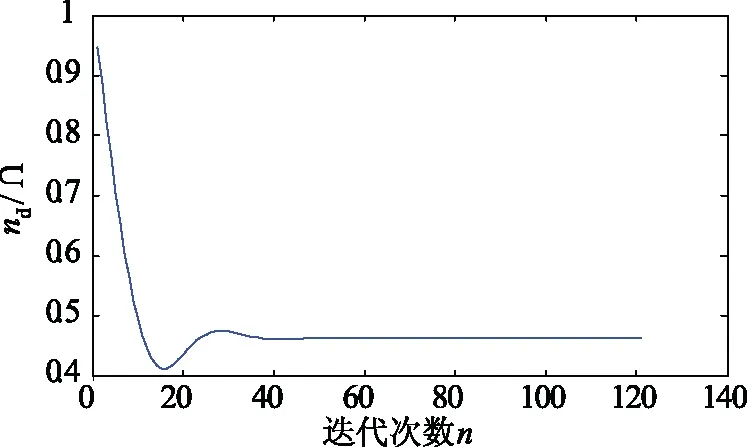
图3 改进算法下电压与迭代次数关系Fig.3 Relation between voltage and iteration times under improved algorithm

通过仿真算例验证了改进算法的可行性，而且在相同工况条件下，对松弛因子ω和迭代次数n的函数关系进行了分析，其函数关系如图4所示，在ω=0.82，存在最小迭代次数n=25。

分析可知：在相同运行条件下，松弛因子直接影响改进算法的迭代次数，较小的松弛因子由于严格约束迭代向量的更新，相应会增加迭代次数；而较大的松弛因子导致改进算法的不收敛性增加，也会增加迭代次数；因此最优松弛因子不仅保证算法的收敛，而且能够加快算法运行速度。

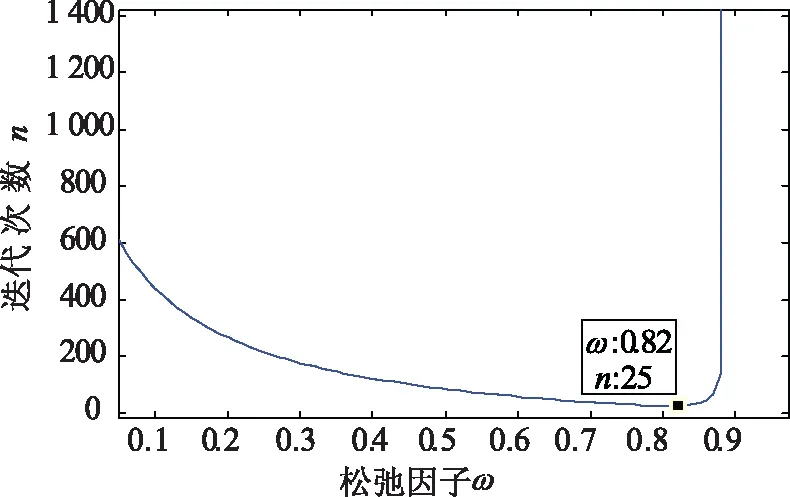
图4 迭代次数与松弛因子关系Fig.4 Relation between iteration times and relaxation factor

根据改进潮流算法对配电网进行故障潮流计算，其结点电压和负载电流如表1所示。

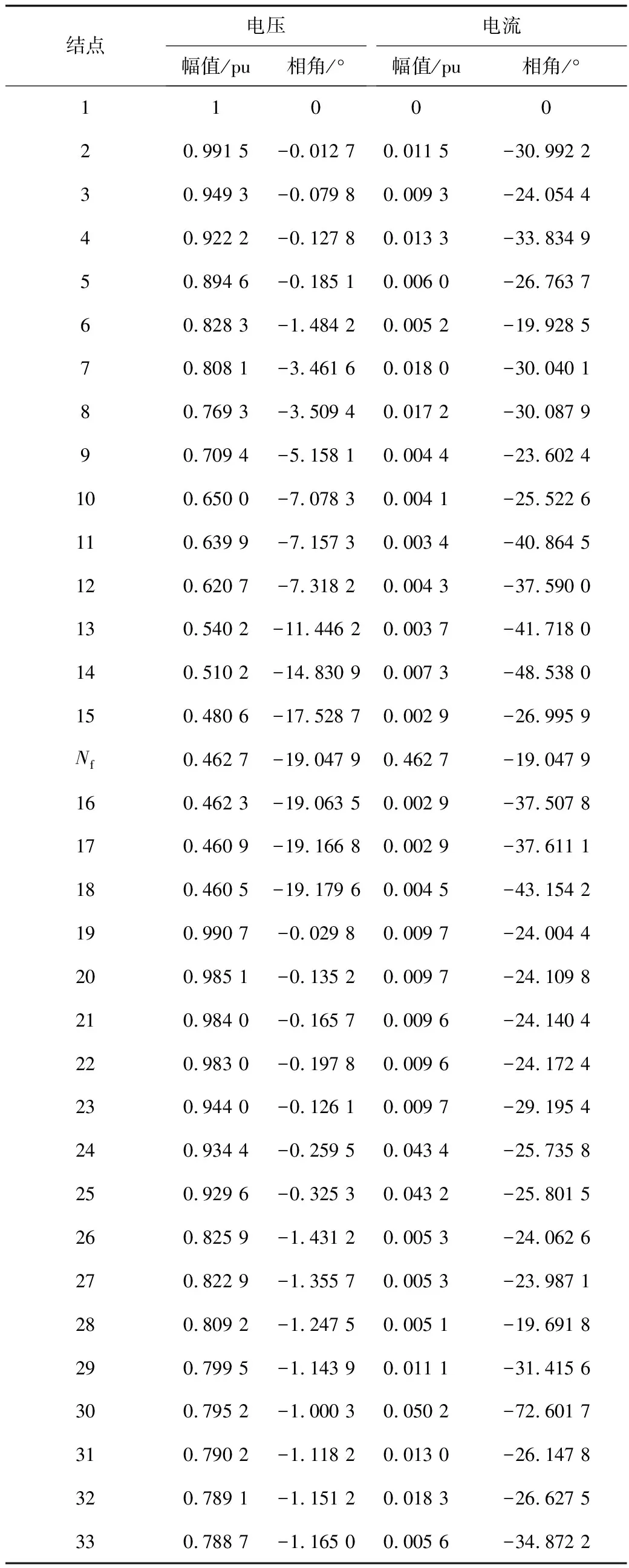
表1 计算结果Tab.1 Calculation results

4 结束语

前推回代潮流算法针对正常运行的配电网具有较好的实用性，但是对于配电网故障潮流的计算却存在不收敛现象。文中从本质上分析了此算法的数学原理以及不收敛的原因，在传统算法的基础上对其进行了改进；通过添加松弛因子，对迭代向量进行约束，从而改变了算法的收敛性。通过在Matlab上进行算例分析，验证了此算法的实用性和收敛性，并且提出了最优松弛因子的理念，但是对于不同故障条件下，针对最优松弛的选取问题，仍需要进一步研究和分析。