大跨连续刚构桥系梁地震响应分析

曾金明

(中交第二公路勘察设计研究院有限公司 武汉 430056)

随着科学技术、国民经济和交通事业的发展，我国西南、西北公路和铁路的兴建，由于很多桥梁不得不跨越河谷和深沟，地形复杂、山高坡陡，大都采用高墩，使桥式更为经济合理。由于连续刚构桥墩高较高，其抗震性能较为复杂，因而对其抗震性能的研究较为重视，其中目前对大跨连续刚构桥的地震响应研究集中在行波效应、多点激励、桩-土模型[1-2],以及高低墩动力性能等方面。而对于双薄壁墩间设置系梁[3-4]对其地震响应影响的研究较少。

本文首先以单个桥墩为研究对象，分析系梁参数对桥墩内力的影响；然后以整个桥梁结构为研究对象，基于Perfom-3D有限元软件，分析系梁进入屈服后对桥墩内力的影响，为大跨连续刚构桥的抗震设计提供一定的依据。

1 系梁参数对桥墩内力的影响

1.1 系梁数量设置

建立力学分析模型时，桥墩高度为30 m，采用圆形截面，直径为1.6 m，桥墩肢间距为5.6 m，上部结构的重量以集中质量的形式施加于墩顶，考虑上部结构作用在一个桥墩墩顶的集中质量是3 000 t，为了分析设置系梁道数对桥墩内力的影响，系梁采用直径为1.4 m的圆截面，桥墩和系梁均采用C40混凝土。系梁沿着横桥向进行布置，设置1道系梁时，系梁布置在桥墩高度的中间，设置2道系梁时，系梁分别设置在桥墩高度的1/3,2/3处，考虑与墩顶质量相同大小的水平力,对3种力学模型进行受力分析，分别为①无横系梁；②设置1道系梁；③设置2道系梁。其弯矩图见图1。

图1 考虑系梁设置模型的弯矩图(单位：kN·m)

由图1可见，与无横系梁模型相比，设置1道系梁的桥墩最大弯矩减小了41.48%，设置2道系梁的桥墩最大弯矩减小了56.68%，因此，通过设置系梁可有效减小桥墩弯矩。

1.2 系梁与桥墩刚度比值

为研究系梁刚度对桥墩内力的影响，按照2道系梁设置时，系梁截面直径分别取1.2，1.4和1.6 m，这时，系梁与桥墩的抗弯刚度之比分别为0.3,0.6和1。

对上述设置的3种力学模型进行受力分析，得到的弯矩图如图2所示。

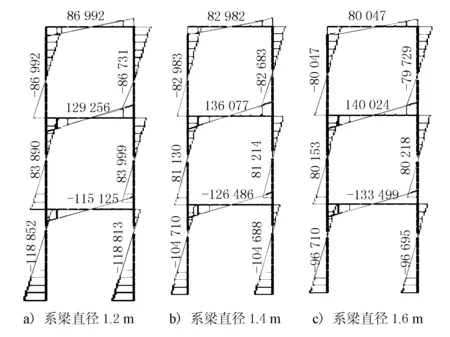
图2 考虑刚度模型的弯矩图(单位：kN·m)

由图2可见，随着系梁刚度的增大，桥墩弯矩值逐渐减小。与系梁截面直径1.2 m相比，当系梁截面直径为1.4 m时，桥墩最大弯矩值减小了11.89%；当系梁截面直径为1.6 m时，桥墩最大弯矩值减小了18.63%。

2 桥梁模型的建立及动力特性分析

2.1 有限元模型的建立

主桥为95 m+180 m+95 m的连续刚构桥。主桥桥墩采用双肢矩形空心墩，顺桥宽度为3.5 m、横桥宽度为9.0 m、壁厚均为0.9 m，墩间距为7.0 m，墩高为80 m。

在混凝土桥墩中，合理定义桥墩的恢复力模型[5-6]对准确模拟桥墩的非线性十分关键。本文定义分析系梁设置对桥梁顺桥方向的非线性地震响应影响，故桥墩纤维只针对顺桥方向进行条形划分。一般桥梁设计中要求桥梁的上部结构处于弹性，而历次的地震震害也表明上部结构一般不会发生明显的破坏，所以主梁采用弹性单元。不考虑桩-土相互作用效应，在墩底固结。

分别建立2种计算模型[7-8]，模型1为不考虑双薄壁墩中的系梁，模型2在桥墩中部处设置系梁，有限元模型见图3。

图3 有限元模型

2.2 动力特性分析

结构的自振特性与结构的质量、刚度大小及分布相关，他们决定着结构的动力响应特性，2种计算模型的前10阶周期如图4。

图4 周期对比图

由图4可见，系梁设置提高了桥梁的整体刚度，即系梁设置后的结构自振周期有所减小。

3 动力增量非线性分析

高墩桥梁由于墩体的自重大，阻尼小，在墩顶还要承受巨大的上部结构传递下来的荷载，就形成了对抗震不利的倒摆式结构，从而桥墩成为抗震的薄弱环节；再者，在地震作用下，由于高墩墩顶产生很大的横向位移，现行《公路桥梁抗震设计细则》规定，一般情况下，桥墩采用反应谱理论计算，对于桥墩高度超过30 m的特大桥梁，可采用动态时程分析法，但是随着理论分析和实验研究的深入，对于高墩桥梁这样几何非线性非常明显的结构，应进行非线性地震响应分析[9-10]。为进一步分析系梁对桥梁非线性地震响应的影响，选择不同场地条件下的7条地震波，其中El-centro地震波的加速度时程曲线如图5所示，选择7条地震波分别对模型1和模型2进行非线性时程分析。限篇幅仅列出El-Centro地震波作用下桥墩地震响应随地震加速度的变化曲线，见图6。

图5 El-Centro地震波加速度时程曲线

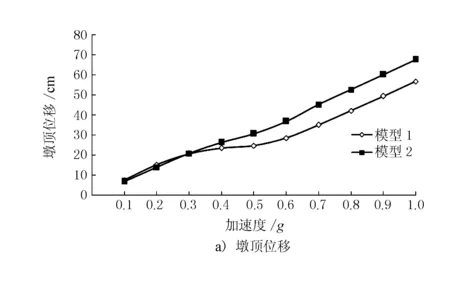
图6 桥墩地震响应变化曲线

由图6可见，随着地震加速度峰值的增加，桥墩的地震响应也随着增加；以墩底曲率为例，在加速度为0.3g时，设置系梁后的墩底曲率增大了49.3%；在加速度为0.7g时，设置系梁后的墩底曲率增大了79.5%；在加速度为1.0g时，设置系梁后的墩底曲率增大了102.6%。

以墩身曲率为例，进一步分析增设系梁对墩身地震响应值的影响。El-centro地震波作用下曲率沿墩身的曲线如图7所示。在该地震波下相对于模型1，模型2的墩身曲率变化率沿墩身的变化情况列于图8，仅以地震波加速度峰值为0.1g和0.5g作用下为例。

图7 曲率沿墩身曲线

图8 墩身曲率变化率曲线

由图7、图8可见，随着地震加速度峰值的增加，墩身的曲率也随之增大；设置的系梁对墩身曲率的影响也在增大；模型1中墩顶和墩底曲率较大，墩身曲率沿着墩身分别由墩顶和墩底向墩身逐渐减小，在墩身中部曲率几乎为0。模型2由于设置了系梁，所以除了墩顶和墩底处的曲率较大外，设置系梁处墩身曲率也较大，甚至超过墩顶曲率；相对于不设置系梁，设置系梁后桥墩曲率增大率在加速度峰值为0.1g时达484%，在0.5g时达到870%；而在桥墩其他部位处的墩身曲率变化相对不明显。增设系梁的桥墩在地震响应分析时，薄弱部位除了考虑墩顶和墩底外，还应当考虑设置系梁处的部位。

为了分析系梁与桥墩屈服的先后顺序，系梁采用纤维模型建立计算模型3，图9为在El-centro地震波作用下，加速度峰值为0.3g时系梁与桥墩墩底的滞回曲线。图10为加速度峰值为0.5g时，El-centro地震波作用下弯矩、曲率沿墩身的变化曲线。

图9 系梁与墩底滞回曲线

图10 墩身弯矩、曲率变化曲线

由图9可见，在加速度为0.3g时，系梁进入屈服，而桥墩墩底处于开裂状态，系梁先于桥墩进入屈服程度。设置适中刚度的系梁，使之在常遇地震下处于弹性范围，可以有效地调整框架内力，减少墩身弯矩；而在设计地震或罕遇地震下能够先于墩身进入塑性状态，通过系梁的损伤来消耗一部分地震动能量的输入，减少下部承重结构的地震反应，保护桥梁结构的安全。

由图10可见，在系梁之上的桥墩部分，模型2的墩身弯矩和曲率大于模型3相应的墩身弯矩和曲率；在系梁之下的桥墩部分，模型2的墩身弯矩和曲率小于模型3相应的墩身弯矩和曲率；从整体来看，相对于模型3，模型2的墩身弯矩和曲率的增大、减小幅度都很小。这说明，虽然系梁屈服有一定的耗能作用，但对实际结构地震影响的程度不大。

4 结论

1) 合理设置系梁可以适当地减小桥墩弯矩值，并且随着系梁刚度的增大，桥墩弯矩减小的程度有所增加，也就是说可以通过系梁的设置，消耗地震的作用，以此来保护桥墩安全。

2) 增设系梁后，在设置系梁处的墩身弯矩、曲率明显增大，甚至超过墩顶的弯矩和曲率，因此在地震作用下系梁设置处的桥墩成为结构抗震设计的薄弱环节。例如，在W1地震波作用下，系梁设置处墩身弯矩为186 910 kN·m，相比不设置系梁增大了332%，超过墩顶弯矩145 950 kN·m。

3) 设置适中刚度的系梁，使系梁先于桥墩进入屈服，消耗了地震能量，提高了桥墩的抗震性能，但是屈服后的系梁对桥墩地震响应的影响很小。