荷载参数对路基边坡稳定性影响数值分析

张宗战

(山西省交通科学研究院 太原 030006)

随着我国经济的高速发展，公路交通量急剧增加，其中车辆大型化和重载等现象会造成边坡发生滑塌、沉降等病害，给公路运营与行车安全带来严重影响[1]。边坡稳定性分析是预防边坡发生破坏的主要决策依据，可确定边坡是否处于安全状态，因此，边坡稳定问题一直受到相关科研者的重点关注[2-3]。近年来，国内学者对荷载作用下边坡稳定性分析方法作了不少研究，但大多为选取最危险截面对路基边坡进行二维分析[4]，忽略了路基土体的三维效应，因此，本文基于有限元强度折减法，运用FLAC3D软件建立边坡数值模型，分别对不同荷载大小、长度、宽度及位置作用下的边坡进行稳定性分析。

1 强度折减法

目前，关于路基边坡稳定性的研究方法主要包括刚体极限平衡法与有限元强度折减法[5]，其中极限平衡法获得的试验结果较为稳定，但仅能得到边坡宏观方面的安全系数，而微观方面的边坡应力、变形及位移均无法进行分析；有限元强度折减法是以强度储备概念为依据，可良好反映路基边坡内的非线性应力-应变关系，其边坡安全系数可定义为初始抗剪强度指标与临界折减强度指标的比值。

(1)

(2)

通过不断调整折减系数K能获得边坡不同状态时的强度参数c′和φ′，然后利用FLAC3D软件对参数进行反复迭代计算，即可得到边坡失稳临界状态时的安全系数Fs。由文献[6]可知，破坏标准一般以摩尔-库仑屈服准则下解的不收敛行为来表征，利用有限元强度折减法对边坡安全系数进行模拟计算时，可将下列3种方法作为边坡失稳的判断依据：①塑性区贯通判据；②位移突变判据；③计算不收敛判据。依据上述失稳判断准则，本文采用折中查找方法，通过对模型进行反复迭代，可计算出路基边坡的安全系数[7-8]。

2 边坡数值模拟

2.1 模型选取

由于边坡稳定涉及的材料均为松散状与黏结状的粒状散体材料，故在路基边坡稳定性分析中通常选用计算高效的摩尔-库仑模型作为本构模型。

2.2 边坡模型及参数

考虑到路基边坡属于条带状结构，为便于模拟计算，试验采用FLAC3D软件建立路基边坡轴对称三维模型，其中路堤高取12 m，沿线路坡长取15 m，路基深度方向和横向均取4 m，路面取1/2为9 m，坡角为45°，有限元计算模型如图1所示。模拟试验的边坡模型共划分成9 620个六面体单元，边坡的土体计算参数如表1所示。

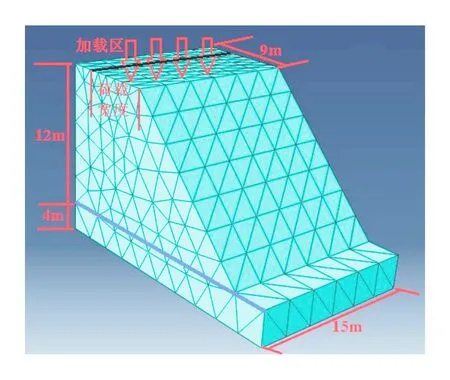
图1 边坡数值模型

项目数值土体容重γ/(kN·m-3)18.1黏聚力c/kPa30内摩擦角φ/(°)32剪胀角ψ/(°)16.5弹性模量E/MPa99.21泊松比μ0.29

2.3 边界条件

模拟计算中假定路基中心线两侧的受力、位移均为正对称，且边坡内各材料性质也相同。将坡体中心对称面和侧面进行水平向约束，路基底面则设定为固定边界。

3 边坡稳定性影响分析

为研究荷载参数对边坡稳定性的影响，试验拟定几种不同荷载参数工况如表2所示，针对不同荷载的大小、长度、宽度及位置情形的路基边坡展开稳定性分析。

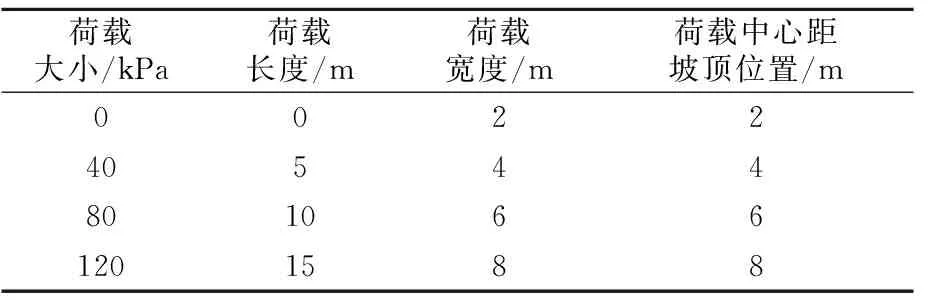
表2 模拟工况

3.1 荷载大小

以荷载长度15 m、宽度2 m、中心距坡顶2 m位置为例，通过对0，40，80，120 kPa 4种不同均布荷载大小下的路基边坡进行稳定性分析，得出安全系数变化曲线，见图2。

图2 不同荷载大小的边坡安全系数变化曲线

由图2可见，在相同荷载长度、宽度及位置情形下，边坡的安全系数随着荷载的增大逐渐减小，其中当荷载增至40 kPa时，边坡安全系数减幅相对较明显，而当荷载继续增至120 kPa时，边坡安全系数减幅大致呈二次非线性变化。

3.2 荷载长度

以荷载宽度2 m、中心距坡顶2 m位置为例，通过对荷载长度分别为0，5，10，15 m的不同荷载大小的路基边坡进行稳定性分析，得出边坡的安全系数变化规律，见图3。

图3 不同荷载长度的边坡安全系数变化曲线

由图3可见，在荷载宽度及位置相同的条件下，当荷载长度增大，不同荷载大小的边坡的安全系数均逐渐减小，其中荷载长度为0 m时，各荷载大小的边坡安全系数均为1.4，当荷载长度增至15 m时，荷载大小为40，80，120 kPa的安全系数分别减至1.32，1.25，1.18，表明边坡的安全系数随着荷载作用长度的增大而逐渐减小，且荷载越大安全系数减幅越明显。

3.3 荷载宽度

试验拟定远坡顶侧的荷载边界依次向路基中心线拓宽，而坡顶侧则维持不变，以荷载长度15 m，荷载大小40，80，120 kPa为例，通过对荷载宽度分别为2，4，6，8 m的路基边坡进行稳定性分析，得出边坡的安全系数变化规律，见图4。

图4 不同荷载宽度的边坡安全系数变化曲线

由图4可见，相同荷载长度、荷载位置情形下，当荷载宽度增大，不同荷载大小的边坡安全系数均呈先减小后平稳变化趋势，其中荷载宽度为2 m时，荷载大小为40，80，120 kPa的安全系数分别为1.3，1.21，1.13，当荷载宽度增至6 m时，不同荷载大小的安全系数分别为1.28，1.19，1.11，当继续增大荷载宽度至8 m时，各荷载的边坡安全系数基本与荷载宽度6 m时相同；通过对比荷载宽度2 m与8 m时的边坡安全系数可知，3种荷载的安全系数减幅均较小(均低于1.77%)。综合上述可知，增大荷载作用宽度仅能略微削弱路基边坡的稳定性。

3.4 荷载位置

考虑到荷载宽度对边坡安全系数的影响不明显，因此试验不再对荷载长度与荷载位置综合作用下的边坡安全系数变化特征作进一步研究。以荷载宽度2 m，荷载大小40，80，120 kPa，荷载长度0，5，10，15 m为例，通过对荷载中心距坡顶2，4，6，8 m位置的路基边坡进行稳定性分析，得出边坡的安全系数变化曲线，见图5。

图5 不同荷载位置的边坡安全系数变化曲线

由图5a)可见，在相同荷载宽度、荷载长度情形下，当荷载中心距坡顶位置增大，不同荷载大小的边坡安全系数均逐渐呈先增大后平缓变化趋势，其中荷载位置增至6 m时，荷载为40,80,120 kPa的边坡安全系数分别增加了7%,10%,13.3%，当荷载位置增至8 m时，边坡安全系数基本维持不变。由图5b)可知，相同荷载大小、荷载宽度情形下，当荷载位置增大，不同荷载长度的边坡安全系数也均按先增后平变化，其中荷载位置增至6 m时，荷载长度为5,10,15 m的边坡安全系数分别增加了1.4%，2.96%，3.76%，当荷载位置增至8 m时，各荷载长度的边坡安全系数保持不变。由此可知，随着荷载中心距坡顶距离增大，荷载大小与荷载长度对边坡安全系数的影响逐渐减小，当荷载位置达到某一定值时，边坡的安全系数不再受荷载中心距坡顶位置影响。

4 结论

1) 相同荷载长度、宽度及位置情形下，随着荷载增大，边坡安全系数逐渐减小。

2) 边坡的安全系数随着荷载作用长度的增大逐渐减小，且荷载越大边坡安全系数的减小幅度越明显。

3) 增大荷载作用宽度仅能略微削弱路基边坡的稳定性。

4) 随着荷载中心距坡顶距离增大，荷载大小与荷载长度对边坡安全系数的影响逐渐减小，当荷载中心距坡顶位置达到某一限值时，边坡的安全系数不再受荷载作用位置影响。