利用时频分析研究非相位锁定脑电活动*

武 侠 钟楚鹏 丁玉珑 曲 折

(中山大学心理系,广州 510006)

1 引言

Berger于1929年第一次记录了人类头皮处的脑电活动(Electroencephalography,EEG,Berger,1929),揭开了对人类EEG研究的序幕。随着时间的推进,研究者们的研究兴趣逐渐从直接研究自发脑电活动转移到了研究事件相关电位(Event-Related Potentials,ERPs)。在1960年代以后,人们主要通过使用时域内ERP分析方法来探讨认知活动和脑电活动之间的关系 (Bastiaansen,Mazaheri,& Jensen,2012)。时域ERP分析方法假设每一次事件诱发的电活动类似,而自发噪音则是随机的。时域ERP分析方法把每一次事件出现的时刻作为数据分析的标准时刻点,将每一个试次(trial)的EEG信号按照标准时刻点对齐后叠加求平均。不同试次的噪音会在叠加平均的过程中相互抵消,叠加平均后的脑电信号就是事件诱发的脑电活动,代表了大脑对该事件的认知加工过程(Luck,2005;Woodman,2010)。

1980年代以来,越来越多的研究者意识到时域ERP成分只是一种特定类型的事件相关脑电信号。事件发生后,大脑对事件认知加工所对应的脑电活动中还有其他类型的事件相关脑电活动。研究者发现,在事件发生后大脑内与事件加工相关的EEG活动有可能是以下几种类型：频率反应(frequency response,Ijspeert,2008),振幅反应(amplitude response,Klimesch,2012; Tallon-Baudry & Bertrand,1999),相位重置(phase resetting,Gruber & Müller,2005; Klimesch et al.,2004),新增成分(additive response,Mäkinen,Tiitinen,&May,2005; Mazaheri & Picton,2005)。

图 1列出了上述四类大脑对事件的反应类型。(1)频率反应(图 1A)是某频率的自发 EEG活动在事件出现后变化了振荡频率,这一类大脑活动多见于单细胞放电或者人们在有节律运动的时候中枢系统某节律细胞的活动。(2)振幅反应(图1B)是事件发生后某频率 EEG自发电活动能量增加(或减小),每个试次中该频率的能量都有所增加(或减小),不过每个试次事件相关电活动相位是随机的,叠加平均时相互抵消掉了,ERP平均波形捕捉不到此类事件相关脑电活动。(3)相位重置(图 1C)是所有试次的相位都会因事件出现而变得一致,这类活动是相位锁定活动。求平均波形时,此类活动会出现在平均波形中,这是我们熟知的ERP成分。(4)新增成分(图1D),即事件发生后每个试次都会出现与自发活动相互独立的新增成分。这些活动的相位相似,强度相似,求平均波形时,也会呈现在平均结果中,也可以产生我们所熟知的ERP成分。

图 1 事件发生后可能的脑电活动变化。

综上,在事件发生后,大脑对事件的认知加工过程可能表现为相位锁定的活动和非相位锁定的活动两类,相位锁定的活动可以通过时域 ERP分析方法来分析,而相位不锁定的活动在时域ERP分析方法中被当作噪音去除掉了。即使是传统的时域 ERP平均波形,也可能有两种产生机制：相位重置(图 1C)和新增活动(图 1D),但这两种机制在传统的时域ERP分析方法中无法区分。为了弥补时域ERP分析方法的这些局限性,研究者们引入了一种新的信号分析方法,这就是本文要介绍的时频分析方法。

2 时频分析方法原理简介

研究者从头皮处的电极记录到的脑电信号是一种时域内的信号,是糅杂了事件诱发的短时暂变信号、自发电活动以及随机噪音等强度随时间变化的信号。为了更加清晰直观地观察脑电信号,可以通过傅立叶变换将信号从时域变换至频域,频域内 EEG活动的各种频率成分可以清晰区分,不仅更直观,而且可以对不同频率成分进行独立分析,给信号分析提供了极大的方便。但实验条件下的EEG信号是一种非稳恒信号,事件诱发的信号有产生和衰减的时间进程。将信号完全转换到频域会失去时变信息,导致频域结果含义不清,难以解释。而时频分析则可以在分析频率成分的同时给出时间信息,使得对时变信号的分析变得直观和容易理解。在结果中包含信号的频域和时域信息的分布被称为时频分布,对信号做时频分布的分析就是时频分析。

时频分析的算法有很多种,包括窗口傅立叶变换,小波变换,Hilbert变换,Hilbert-Huang变换,Wigner-Ville分布等方法(Huang et al.,1998; Torrence& Compo,1998)。在心理学脑电数据分析领域,最常用的是小波变换和Hilbert变换。小波变换常应用于计算各个波段活动的能量(Mishra,Martínez,Schroeder,& Hillyard,2012; Tallon-Baudry &Bertrand,1999)。对相位的计算中,则常会用到Hilbert变换(Canolty et al.,2006; Song,Meng,Chen,Zhou,& Luo,2014)。窗口傅立叶变换也是一种时频分析算法,但高频和低频波段信号的分辨率相同,在心理学脑电数据分析中应用较少。传统的傅立叶变换则是一种频域分析方法,不适合时变信号的分析。

2.1 傅立叶变换和窗口傅立叶变换

为了形象地说明几种时频分析方法的异同,本文构造了两段简单的时变信号：第一段(图2A)的前半段是振幅为1的10 Hz正弦信号,后半段是振幅为 1.5的 20 Hz余弦信号; 第二段(图 2B)的前半段是振幅为1.5的20 Hz余弦信号,后半段是振幅为1的10 Hz正弦信号。这两段不同时变信号的傅立叶变换结果完全相同(分别见图2C和图2D)。由此可见,傅立叶变换对于时变信号并不适用。在实际应用中,傅立叶变换只适用于分析一些能产生相对稳恒的脑电振荡模式的实验数据,如对稳态视诱发(SSVEP)的分析(Regan,1966;Norcia,Appelbaum,Ales,Cottereau,& Rossion,2015; Rossion,Prieto,Boremanse,Kuefner,& van Belle,2012)。

窗口傅立叶变换,又叫短时傅立叶变换(shorttime Fourier transform,STFT,Allen,1977),是在傅立叶变换的基础上,对算法做了改进,从而适用于时变信号的分析。具体来说,是对信号进行分析时,加了一个短暂的时间窗口,在窗口内对信号进行傅立叶变换。因为窗口时间短暂,窗口内的信号可近似看作稳恒信号,通过傅立叶变换就可以得到短暂窗口内的频率信息,然后再将时间窗口依次施加于信号中不同的时间位置,从而获得原信号不同时间位置的频率信息。用窗口傅立叶变换分析图 2A、2B中的时变信号结果如图3A所示。

窗口傅立叶变换中采用的窗口一般是 Hanning窗、Hamming窗或者高斯窗口(Pampu,2011)。选择了窗口后,窗口长度在信号分析过程中便不再改变(如图 5A),于是高频和低频信号有相同的时间分辨率和频率分辨率。

脑电研究表明,低频波段相差数赫兹的频率可能代表了不同的心理功能。比如一项记忆研究中,阿尔法波段(α,8～12 Hz)与记忆的提取相关,而西塔波段(θ,4～8 Hz)与记忆编码相关(Klimesch,1999),两个波段频率只相差数赫兹。对于较高频段,往往较广频段范围内的信号代表了同一种心理功能,比如伽马波段(γ,30 Hz以上)往往是一大段频率具有同样的认知功能(Siegel,Donner,Oostenveld,Fries,& Engel,2008)。这就需要在实际分析脑电信号时,更加希望低频有更高的频率分辨率,而高频则无需追求特别高的频率分辨率。要实现这样的目的,需要采用小波变换。

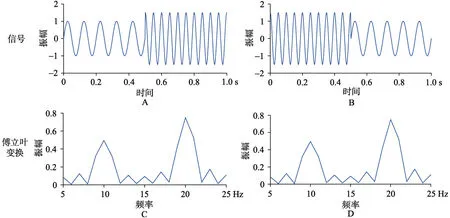
图2 时变信号的傅立叶变换示意图。

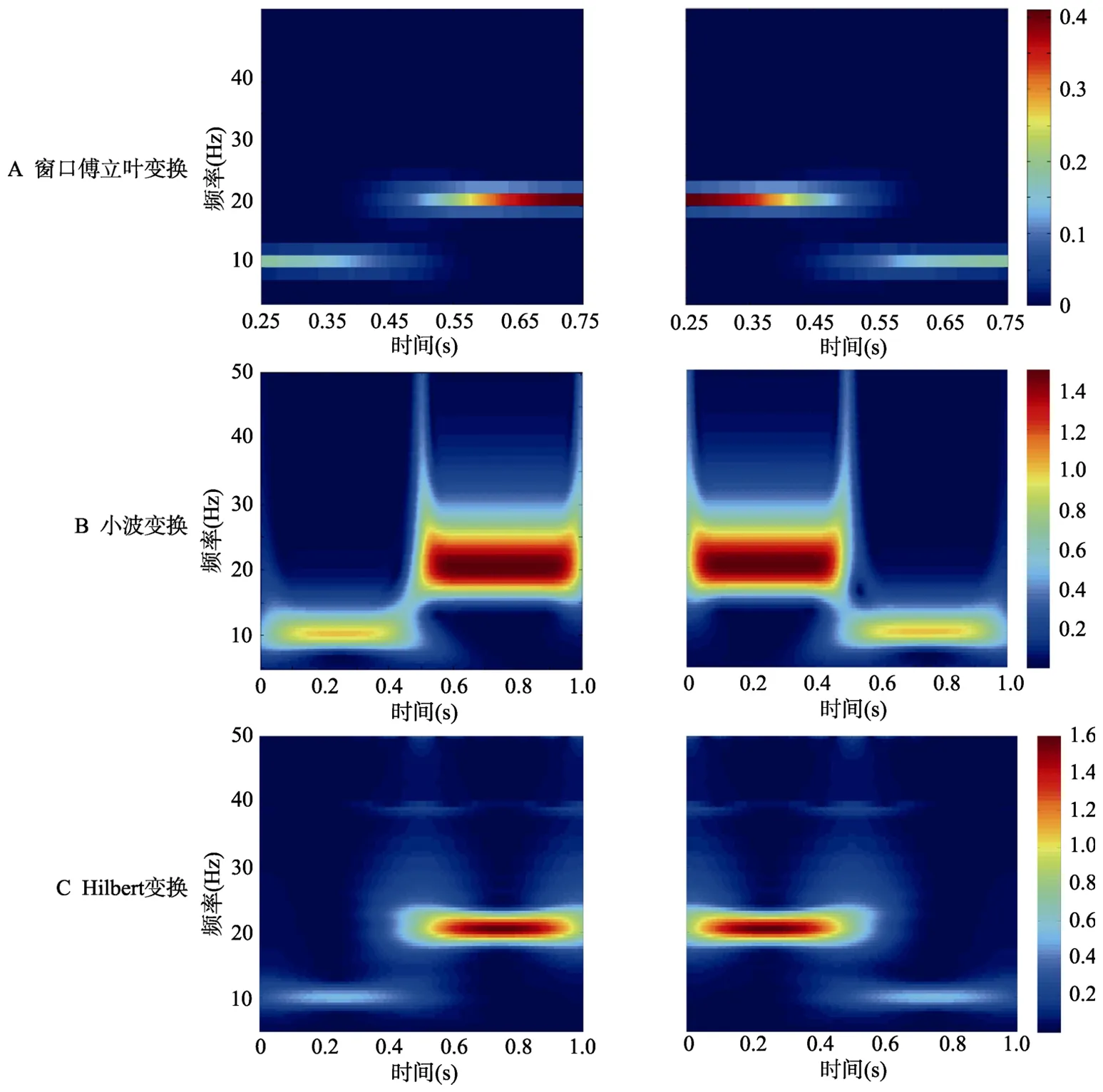
图3 对图2中的两个时变信号的时频分析示意图。

2.2 小波变换

小波是一种时间长度有限并向两端快速衰减的振荡波形(Vidakovic & Mueller,1991)。小波的振荡形态有很多种,每一种形态被称为一种母小波 (Lee & Yamamoto,1994)。构造母小波需满足一定的条件,不同形态的母小波会对分析结果造成影响(Nobach et al.,2007)。所以分析数据时要根据所分析数据的特点,选择合适的母小波(Kharate,Patil,& Bhale,2007; Ngui,Leong,Hee,& Abdelrhman,2013)。脑电研究中最常用的是复morlet小波分析(连续小波分析,Roach & Mathalon,2008)。复Morlet小波可以看做是由余弦振荡为实部和正弦振荡为虚部构成的复振荡函数加一个高斯窗口组成,正余弦振荡向窗口两端迅速衰减(Bernardino& Santos-Victor,2005; Lieuw,2015,图 4)。

图4 复Morlet小波示意图,实线是小波的实部,虚线是小波的虚部。复Morlet小波的实部和虚部相位相差 90度,都可以看做是正余弦信号加了高斯窗口构成的向两端急剧衰减的振荡信号。

信号分析时,Morlet母小波经过压缩和扩张可生成一个小波族(wavelet family,图 5B),不同压缩和扩张程度的小波可以理解为代表着不同“频率”的小波,然后将小波族的子小波分别与信号做卷积,从卷积结果中提取出信号的时频能量和相位。各个子小波具有不同的时间长度,“高频”小波的时间长度比“低频”小波更短,但是两者在各自时间长度内的周期数是一样的。小波分析中低频波段时间窗口长,频率窗口短,因而可以得到较高的频率分辨率但时间分辨率较差; 而高频波段,时间窗口短,频率窗口长,因而有较高的时间分辨率和较差的频率分辨率(图 5B)。对图 2的两个时变信号做小波变换结果如图3B所示。

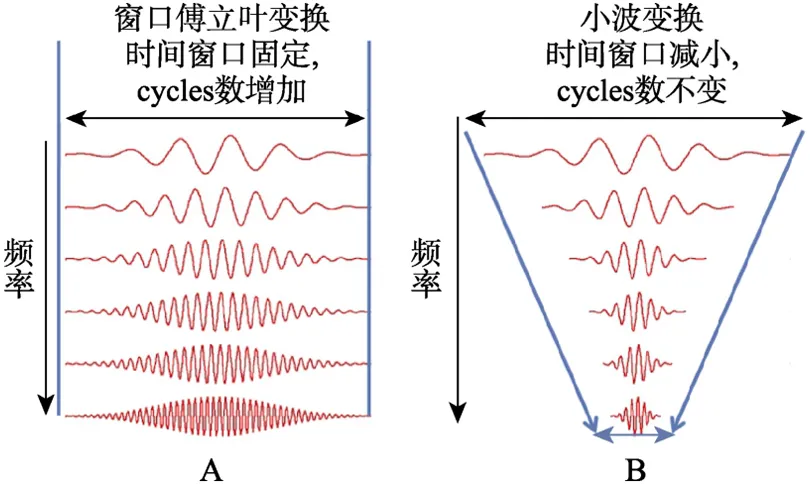
图 5 窗口傅立叶变换和小波变换小波族(wavelet family)子小波对比。

2.3 Hilbert变换

Hilbert变换是将信号与1/(pi×t)做卷积,使得信号的相位旋转 90度,而本身的振幅大小不变(Nobach et al.,2007)。心理学领域的数据分析中,Hilbert变换的应用亦很广泛(Canolty et al.,2006;Penny,Duzel,Miller,& Ojemann,2008; Song et al.,2014)。在EEG数据分析中,Hilbert变换主要是通过解析信号的构造来求解信号的能量和相位的。Hilbert变换常和滤波结合在一起用,通过无相位偏差的带通滤波将要分析的信号限定在所要分析的较窄频段内,然后再由Hilbert变换求解该频段信号的振幅和相位大小(Song et al.,2014)。一般认为,Hilbert变换拥有较高的频率分辨率,而时间分辨率稍差,在边界处的计算误差(边界效应)比较大。一些研究者采用了信号两端补零和加Hanning窗的办法减少 Hilbert变换的边界效应(Song et al.,2014)。Hilbert变换对图2中的时变信号的分析结果如图3C所示。

总之,窗口傅立叶变换、小波变换以及 Hilbert变换都可以有效地分析时变信号(如图3所示)。有研究者对比了窗口傅立叶变换、小波变换以及Hilbert变换对一批脑电数据分析的结果,发现在三种方法之间并没有实质的差别 (Bruns,2004)。

3 时频分析的基本计算指标和心理学意义

时频分析技术通过丰富的计算指标揭示脑电中非相位锁定成分的心理意义。不同计算指标帮助揭示认知加工过程的不同方面。这部分内容将简要介绍时频分析用于脑电分析的三大类指标：能量,相位一致性以及耦合。

3.1 能量(Power)

3.1.1 计算原理

能量是指信号分析结果中某频率成分在某时刻点的能量值,代表了该频率成分振荡强度(振幅亦可以代表振荡强度,为能量的平方根)。以小波变换求能量为例,分析能量前,首先构造合适的母小波,母小波由小波核心参数Q值决定。感兴趣的频段为低频时,Q一般选为5,或者3 (Mishra et al.,2012); 若感兴趣的频段为高频时,Q可以选择为6或者7。也有文献提出可以调节Q值的小波变换(Selesnick,2011)。母小波构造好后,根据要分析的频段确定具体频率值和对应尺度值,然后根据尺度值构造子小波。将子小波和信号做卷积运算,对卷积结果中的小波分析系数求模平方即为能量值,而系数模则为振幅值。

3.1.2 能量的心理学意义

在数据分析过程中,时频分析求能量有两种求解顺序,分别对应不同的事件相关脑电活动(图6)：一种是先对不同试次的信号叠加平均得到平均波形(ERP),然后求平均波形的能量(evoked能量,代表相位锁定于刺激发生时刻的能量); 另一种是求单个试次的能量,然后把不同试次的相应时频能量进行叠加平均(包含了 evoked能量和induced能量)。由此可见,时频分析比传统的时域ERP分析方法可以挖掘出更多的事件诱发脑活动,弥补了传统方法的局限。在 Tallon-Baudry和Bertrand (1999)的研究中,induced γ活动代表了被试对三角形的整体觉知,代表了一种对特征的整合,这是evoked能量所无法揭示出来的。后来的研究者使用了不同的刺激,仍然得到了相似的结论,刺激之后200 ms后出现的非相锁的induced γ活动标志着物体的特征整合在一起(Busch,Herrmann,Müller,Lenz,& Gruber,2006; Goffaux,Mouraux,Desmet,& Rossion,2004; Gruber,Trujillo-Barreto,Giabbiconi,Valdés-Sosa,& Müller,2006; Martinovic,Gruber,& Müller,2007; Tallon-Baudry,2009)。不仅如此,也有研究发现γ能量在工作记忆中也标志着特征整合的过程(Morgan et al.,2011; Tseng,Chang,Chang,Liang,& Juan,2016)。

图6 计算evoked能量和induced能量示意图,

虽然有研究表明,induced γ活动可能受到微眼动的影响(Yuval-Greenberg,Tomer,Keren,Nelken,& Deouell,2008; Muthukumaraswamy,2013),但大量的研究在使用一些数据分析技术去除了微眼动对研究结果的影响后,同样发现了特征捆绑过程中γ活动的存在(Hassler,Barreto,& Gruber,2011;Keren,Yuval-Greenberg,& Deouell,2010)。这说明了刺激出现200ms后持续较长时间的γ活动与特征捆绑相关,这种 γ活动代表了一种将大脑加工的特征信息整合起来的过程(Hassler,Friese,Martens,Trujillo-Barreto,& Gruber,2013; Makin et al.,2011)。

α能量是较早被发现和研究最广泛的波段之一。α能量在清醒闭眼的时候比较显著,是清醒时大脑后部区域能量最为显著的波段(Valipour,Shaligram,& Kulkarni,2013)。大量研究发现α与注意密切相关,α能量低预示着注意状态(Sharma& Singh,2015; Marshall,O’Shea,Jensen,&Bergmann,2015; Capilla,Schoffelen,Paterson,Thut,& Gross,2014; Händel,Haarmeier,& Jensen,2011; Hanslmayr,Gross,Klimesch,& Shapiro,2011; van Gerven & Jensen,2009),比如选择性注意的研究中发现了α能量的高低预示着注意选择过程。在使用Posner中央线索范式来研究空间选择性注意的文献中,人们发现线索提示后约500ms (此时目标尚未出现),会在提示空间对侧枕区皮层诱发比同侧更低的 α能量,代表了对线索提示位置的注意增强(Kelly,Gomez-Ramirez,&Foxe,2009; Kelly,Lalor,Reilly,& Foxe,2006;Rihs,Michel,& Thut,2007; Sauseng et al.,2005;Thut,Nietzel,Brandt,& Pascual-Leone,2006;Worden,Foxe,Wang,& Simpson,2000)。不仅如此,在一项外周 Posner线索任务中,无关声音刺激在左右视野空间出现,也会引起目标出现前线索对侧大脑皮层枕区 α能量的降低。说明了在外周Posner任务中,α能量的减小同样代表了被试对一侧空间的注意(Störmer,Feng,Martinez,McDonald,& Hillyard,2016)。除此之外,在基于特征的注意和基于物体的注意研究中都有类似的发现,即特征加工相应脑区或者物体加工相应脑区α能量的降低代表了对该特征或物体的注意 (Snyder &Foxe,2010; Knakker,Weiss,& Vidnyánszky,2015;Fu et al.,2001)。在情绪性注意的研究中,也有类似的发现,即 α能量大小预示着对情绪刺激的注意和抑制(Uusberg,Uibo,Kreegipuu,& Allik,2013)。

定位于前额中区的 θ能量则被发现与认知控制功能有关(Cavanagh,Cohen,& Allen,2009;Cavanagh,Frank,Klein,& Allen,2010; Womelsdorf,Johnston,Vinck,& Everling,2010)。比如在2013年的一篇研究中,研究者使用多任务的视觉游戏来训练老年人,发现多任务视觉游戏训练后,老年人额中区的θ能量以及额中区θ相位和枕区的θ相位联系增强,说明了增加的额中区能量对视觉任务的完成有更好的认知控制作用(Anguera et al.,2013)。此外,有研究发现β能量与运动密切相关(Engel & Fries,2010; Bai et al.,2008; de Lange,Jensen,Bauer,& Toni,2008; Waldert et al.,2008),也有一些研究发现β能量与被试的注意有关(Gola,Magnuski,Szumska,& Wróbel,2013; Deiber,Ibañez,Missonnier,Rodriguez,& Giannakopoulos,2013)。

3.2 相位一致性(Phase Locking Index,PLI)

3.2.1 计算原理

相位一致性(PLI)是对某电极大量试次间相位一致性程度的衡量。相位一致性代表着大量试次在事件发生时刻以及后续较短时间内,相位在试次间是否一致。如果相位完全一致,PLI为1,相位完全随机,PLI则为0。计算时,将不同试次的某时刻相位用单位向量表示,然后计算不同试次间该向量的平均值,原理如图7。

3.2.2 相位一致性的心理学意义

时域 ERP成分和相位一致性有密切的关系(Busch,Dubois,& VanRullen,2009; Mathewson,Gratton,Fabiani,Beck,& Ro,2009)。相位一致性指标可以和能量指标结合起来,用于探讨ERP产生的机制 (Makeig et al.,2002; Mishra et al.,2012)。如前所述,ERP成分有两种可能的产生机制：相位重置(图 1C),和新增成分(图 1D)。一种区分两种机制的方法是检测刺激出现前后每个试次中的能量以及相位一致性; 如果前后能量没有明显不同,但是平均结果中却有明显的ERP成分,那么便可以肯定相锁机制的存在; 如果刺激出现后单个试次的能量有明显增加,且有中等强度的相位锁定性,那么可能说明新增成分机制的存在。但在实际的研究中,ERP机制的分析还会受到α阻断效应的干扰(Mazaheri & Picton,2005; Mishra et al.,2012),增加了区分ERP机制的难度。大量研究者使用了更多的方法来尝试区分ERP产生的机制(Becker,Ritter,& Villringer,2008; Mazaheri &Jensen,2006)。其他脑功能成像技术也能从探讨ERP产生的机制中获得启发,Fell (2007)指出为了进一步理解事件相关 EEG和 fMRI之间的关系,将振幅和相位分离将是至关重要的步骤。

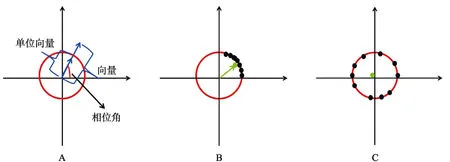
图7 PLI计算原理示意图,

此外,相位一致性还代表大脑认知加工过程的一些特点,如有文献指出,α活动的相位一致性指标标志着α活动相对于刺激输入的一种初始化,能够增强刺激随后加工的强度(Hebert,Lehmann,Tan,Travis,& Arenander,2005)。海马中振荡活动的相位锁定性还和工作记表现有关(Kleen et al.,2016)。

3.3 耦合(Coherence)

耦合是时频分析应用到EEG数据分析领域最广泛的指标之一。耦合是计算不同电极间同步活动的指标,反映了认知加工过程中的一种整体网络功能(Bowyer,2016; Cabral,Kringelbach,& Deco,2014; Greenblatt,Pflieger,& Ossadtchi,2012)。有多种不同的耦合指标,如同频率信号相位之间的耦合(即相位同步性),不同频率振幅/能量之间的耦合,低频信号相位和高频信号能量之间的耦合等。这些耦合指标分别反应不同的神经网络活动特点(Lachaux,Rodriguez,Martinerie,& Varela,1999; Siegel et al.,2008; Canolty et al.,2006;Canolty & Knight,2010; Jensen,Bonnefond,&VanRullen,2012; Penny et al.,2008)。本部分内容主要介绍同频率信号不同电极间的相位同步性以及低频相位和高频能量之间耦合的计算原理和心理意义。

3.3.1 不同电极同频率信号的相位同步性(Phase Synchrony)的计算原理

大脑加工信息以一种网络化的方式进行,一个直接的证据就是相距较远的脑部区域间的脑电信号存在耦合。远距离电极间同频率信号的相位同步变化被称为相位同步性(Phase Synchrony,Lachaux et al.,1999),是两个电极同频率信号对应试次间相位差恒定性程度的衡量。对应试次间的相位差越稳定,相位同步性越好,反之,相位同步性越差。计算时,需要计算出两电极对应试次对应时刻某频率的相位值,然后相减。将此相位差异用复平面内的单位向量表示,不同试次之间的相位差对应的单位向量的末端分布在单位圆上。如果相位差异接近恒定,那么这些单位向量的平均向量的长度便会接近于 1; 反之,相位差分布随机,平均向量的长度便会接近于0。平均向量的长度就是两电极相位同步性的指标。计算原理如图8所示。

3.3.2 相位同步性的心理学意义

相位同步性体现了长距离脑区的同步活动,反映了自下而上或者自上而下的信息传递和相互控制。有研究指出无论休息状态还是任务状态,不同波段的相位同步性普遍存在于脑电活动中(Pockett,Bold,& Freeman,2009)。Siegel将长距离的相位同步性视为神经网络功能的一个标志(Siegel et al.,2008)。Finger的研究也表明,相位同步性可能是大脑将分散于不同区域的信息整合在一起形成一个整体的主要机制(Finger & König,2014)。在一个需要左右大脑半球共同加工视觉信息形成整体知觉的研究中,由小字母组成的大字母横跨左右视野,在需要认出大字母的实验条件中,左右半球电极间表现出了相位同步性的增加,两个半球的信息得到了整合(Rose,Sommer,&Buchel,2006)。老年人在多任务游戏中额中区和枕区的长距离 θ相位耦合代表了高级脑区对低级脑区的认知控制(Anguera et al.,2013)。在关于注意的研究中,发现不同脑区间的 γ活动相位耦合与注意活动有关(Doesburg,Roggeveen,Kitajo,&Ward,2008)。而一项研究则表明双任务中α活动相位同步性则是注意负载强弱的指示器(Kwon et al.,2015)。也有研究表明,α相位同步性与认知任务的表现有关(Palva & Palva,2011)。而γ活动同步性则还与对物体的意识相关(Castelhano,Rebola,Leitão,Rodriguez,& Castelo-Branco,2013)。在视觉短时记忆中,也发现了纹外皮层的 β活动同步性指标与短时记忆保持的相关 (Tallon-Baudry,Bertrand,& Fischer,2001)。此外,相位同步性也是标记一些疾病的重要指标,可能暗示着病人的神经网络功能的紊乱。一些研究表明癫痫病人发病的时候相位同步性会有一个很大的增长 (Franaszczuk& Bergey,1999),另外的研究也表明精神分裂症病人的γ同步性指标异常(Spencer et al.,2003)。这些不同的研究都说明相位同步性体现了大脑的各功能区联合为网络而显现出更高级的认知功能,可以帮助人们完成复杂的认知任务。

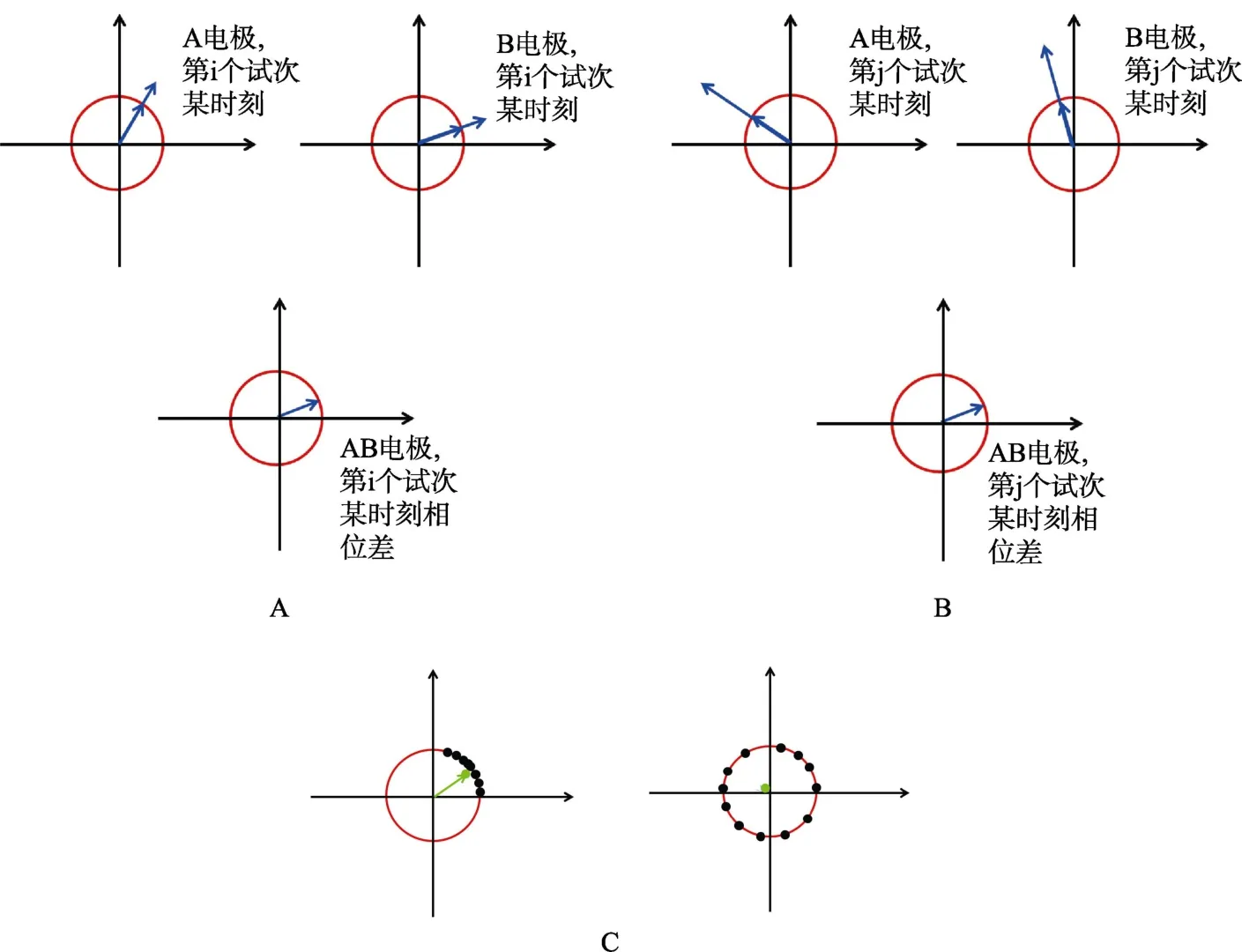
图8 不同电极相位同步性计算原理示意图。

3.3.3 低频信号相位和高频信号能量之间的耦合(Phase-Amplitude Coupling,PAC)的计算原理

有研究指出,长距离脑区间的调控多借助于低频振荡,而高频信号往往是局部活动的一种体现(Canolty & Knight,2010),低频和高频之间的耦合就具有了特殊的功能意义,局部脑加工体现局部的大脑的模块化加工,而与长距离的低频信号的耦合代表一种网络的信息整合。这种耦合在数据中表现为高频能量的高低起伏有一定的周期性,与信号中低频成分的相位变化相关(图9A)。

这种耦合的计算方法有很多(Penny et al.,2008; Samiee & Baillet,2017),其中一些研究给出了一种相对灵敏的计算方法(Canolty et al.,2006;Song et al.,2014)。首先,计算出原信号中的高频信号(如 γ)的振幅 ampγ(t)和低频信号(如 θ)的相位phaseθ(t),每个对应时刻的高频能量和低频相位组成的复数 ampγ(t)·ephaseθ(t),在复平面内对应一个点(图 9B),许多个时刻的点构成了一个分布(图9C和 9D),如果复数点的分布偏向于一个象限,那么就说明高频能量多分布在某一个相位角内,两者有耦合(图 9C),否则低频相位和高频能量则无耦合(图 9D)。实际计算时,还需要用置换检验(permutation test)的方法衡量耦合的相对强度(Canolty et al.,2006)：

3.3.4 低频相位高频能量耦合的心理学意义

低频相位和高频能量的耦合反映了多种认知机能,在不同的认知任务中都可能有相应表现。该耦合可能反映了这样的机制,将信息从大的行为反应时间尺度转移到局部的尺度,进行进一步的运算和突触修饰,从而整合多个时空尺度功能(Canolty & Knight,2010; Jensen et al.,2012)。Bonnefond等人关于α相位和γ能量的耦合研究说明信息自上而下的门控机制,局部的信息计算被约100 ms的时间周期门控控制,提供了周期性抑制的控制作用(Bonnefond & Jensen,2015); 而在另外一项研究中,研究者使用了不同的行为任务,发现低频θ相位和高频γ能量的耦合模式直接和行为任务有关,在不同的行为任务中,表现出不同脑区间的耦合,说明进行不同任务时不同大脑区域之间的信息交流(Canolty et al.,2006)。认知任务中,高级脑区对低级脑区的认知控制可以体现在高级脑区的低频振荡活动相位与低级脑区的高频振荡能量的耦合上(Helfrich & Knight,2016)。不仅如此,在工作记忆任务中,长距离的低频相位(θ、α)和高频能量(β、γ)耦合以及长距离的低频相位的耦合反映了不同脑区之间的信息交流(Daume,Gruber,Engel,& Friese,2017)。在一篇关于儿童工作记忆的研究中,研究者通过对儿童工作记忆的训练发现认知控制区域(额顶区)的 α相位和低级脑区(颞区)的γ活动的耦合增强,提示了该类型的耦合在工作记忆中的作用(Barnes,Nobre,Woolrich,Baker,& Astle,2016)。动物研究也表明海马记录到的低频θ和高频γ的耦合与学习和完成回忆任务有关(Tort,Komorowski,Manns,Kopell,&Eichenbaum,2009)。还有文献指出低频相位和高频能量耦合在记忆中标志着编码的功能(Friese et al.,2013)。工作记忆中(短时记忆)的信息编码以及容量也可以用这类耦合解释(Axmacher et al.,2010)。最近的一项研究中,发现了慢波睡眠阶段的慢波振荡活动的相位与纺锤波之间的耦合在睡眠记忆巩固中有重要的作用,可以部分解释老年人记忆巩固能力的衰退(Helfrich,Mander,Jagust,Knight,& Walker,2018)。

总的来说,低频相位和高频能量耦合是当前研究的一个热点,在不同任务以及不同状态都可以发现这样的活动模式,说明这种耦合反映了脑内不同大脑区域之间的信息交流以及信息控制,从而帮助被试完成各种高级认知任务,反映了大脑加工信息时的网络功能。

4 小结

时频分析是当前心理学脑电领域的一个热点算法应用。它可以帮助我们捕捉脑电信号中非相位锁定于事件发生时刻的活动,可以将事件诱发脑活动的探索拓展到刺激出现前。心理学脑电数据分析领域应用最多的时频分析算法是复 Morlet小波变换和Hilbert变换。时频分析在脑电数据分析领域的应用主要体现在一些指标上。不同频段的能量指标反映了不同的认知过程,如 α能量与选择性注意密切相关,而 γ能量则与特征捆绑密切相关。相位一致性指标往往被用来探讨时域ERP成分产生的机制。耦合往往反映了大脑作为一个网络体现出来的整体功能,同频率远距离脑区之间的相位耦合和低频相位和高频能量的耦合是过去研究中的两个热点。未来可以关注时频分析技术在非任务态(静息态)中的应用以及其他耦合指标(如不同频段能量之间,不同频段相位之间)在探索心理过程中的应用。