基于水下爆炸能量输出特性的小型组合装药起爆元件等效评估

吴建宇，谢兴博，钟明寿，宋 歌，王 敏，李 营



基于水下爆炸能量输出特性的小型组合装药起爆元件等效评估

吴建宇1，谢兴博1，钟明寿1，宋 歌1，王 敏1，李 营2

(1. 陆军工程大学野战工程学院，江苏 南京，210007；2. 海军装备研究院，北京，100161）

为了提高用于模型试验的小型组合装药水下爆炸测试的可靠性和精确性，对由电雷管和扩爆药柱作为起爆元件共同起爆TNT药柱进行了水下爆炸测试，基于能量输出的等效原理，得到了起爆元件的TNT等效换算质量。结果表明：当主装药质量较小时，起爆元件对组合装药能量输出的影响十分明显，通过与炸药水下爆炸能量输出经验值的比较，验证了本文提出的等效换算方法的可靠性；就本文的试验工况而言，边界条件对于气泡最大膨胀半径的影响可以忽略不计，但随着装药整体质量的增大，一次气泡脉动周期的试验值与理论值的差距会显著增大。

水下爆炸；起爆元件；冲击波能；气泡能；等效换算

水下爆炸试验是研究水中兵器爆炸威力的重要手段，虽然原型试验最接近真实的试验条件，但其准备周期长、耗资巨大且所获得的数据相对有限。根据相似理论，模型试验可以还原出与原型试验相近的结果，且操作性与可重复性更强。由于不同模型试验条件的限制，可用于试验的最大装药量不尽相同。当装药量较小（如10g）时，为确保其可靠完全起爆，常采用雷管结合辅助件（如扩爆药柱、导爆索等）起爆的方式。此时，起爆元件对于装药整体输出能量的影响不可忽略，需要结合水下爆炸能量输出特性对起爆元件进行等效换算，以便于将模型试验还原为原型试验，并将测试数据应用到理论计算或数值仿真中。

炸药水下爆炸后，其能量输出主要为冲击波能和气泡能，其中水下爆炸冲击波具有高频特性，其峰值高且衰减迅速，而气泡载荷压力低，且持续时间长[1]。关于炸药水下爆炸能量的测定，研究人员做了大量的工作。杨振[2]开展了针对舰船缩比模型的水下爆炸测试，证明了基于爆炸相对能量的评估方法比基于冲击波压力峰值的评估方法具有更高的精度；牟金磊[3]证明了炸药水下爆炸的有效比冲能仍满足相似率；秦健等[4]证明了炸药在水下爆炸能量输出过程中存在较大的能量衰减；王秋实[5]、封雪松[6]和杨斐[7]对含铝炸药的水下爆炸性能进行了水下测试；万晓智等[8]开展了高铝含量薄膜炸药与铝粉炸药水下爆炸性能的对比试验。以上研究均未涉及小型组合装药起爆时起爆元件对装药整体能量输出性能的影响。

本文基于炸药水下爆炸能量输出的等效特性，对由电雷管和扩爆药柱作为起爆元件的小型组合装药开展水下爆炸测试分析，研究考虑用于模型试验的小型组合装药起爆元件等效药量转换问题。

1 水下爆炸基本理论

1.1 冲击波参数

水下爆炸发生后，炸药化学能瞬间转变为爆炸能并形成高达3 000℃的气体，其产生的压力高达5 000MPa。冲击波以球形波的形式在水中传播，其传播至结构表面时由水下爆炸产生的冲击能可以由药量和炸高的函数表达出来。根据经典的Cole理论，水下爆炸在给定点的冲击波压力呈突跃状，并伴随着指数规律变化的衰减[9]，其表达式如下：

式（1）中：()为压力任意瞬时的压力，Pa；为时间衰减指数，μs；为冲击波头到达目标点的时间。P和的表达式分别如下：

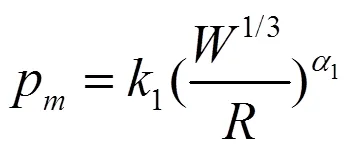
式（2）~（3）中：为炸药药量，kg；为测试点到爆心的距离，；1、2、1、2均为炸药水中爆炸相似常数和系数，针对TNT炸药，1=52.4MPa，1=1.13，2=0.084ms，2=-0.23。

1.2 有效比冲能

冲击波有效比冲能可表示为：

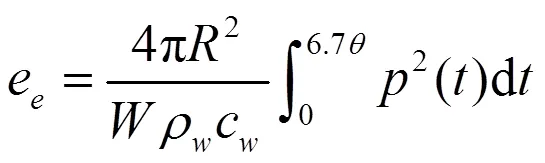
将式（1）~（3）代入式（4）得到有效比冲能为[3]：

1.3 有效比冲能的试验测定

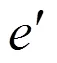
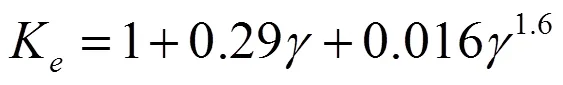
式（8）中：为压力传感器的直径，m。冲击波在传播过程中有部分能量转化为热能及其它能量耗散，为冲击波衰减系数，与装药的C-J压力CJ（Pa）有关，其表达式为[11]：

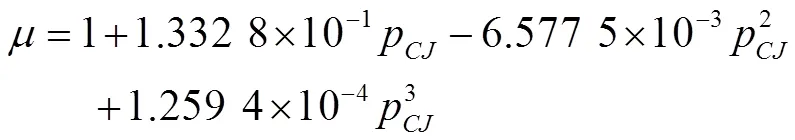
1.4 气泡能

气泡能的计算可以用水下爆炸时生成的气体产物克服静水压第1次膨胀达到最大值时所做的功来度量[3]。单位质量炸药释放的气泡能e(简称比起泡能，J/kg)为：

式（10）中：max为气泡第1次膨胀到最大时的半径；0为爆心处的静水压力，Pa。

1.5 总能量

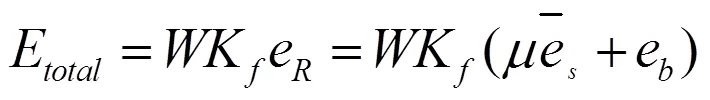
式（11）中：K为炸药形状修正系数。对于非球形装药取1.02~1.10，考虑到试验中用到的炸药规格不同，选择1.06作为装药形状的平均修正系数。

2 等效换算方法

本研究在C.F.Huang[12]换算方法的基础上综合考虑冲击波能和气泡能，建立改进的等效换算方法。试验用小型组合装药如图1所示，由8#工业电雷管、聚黑-14药柱（扩爆药）和TNT药柱（主装药）组成。

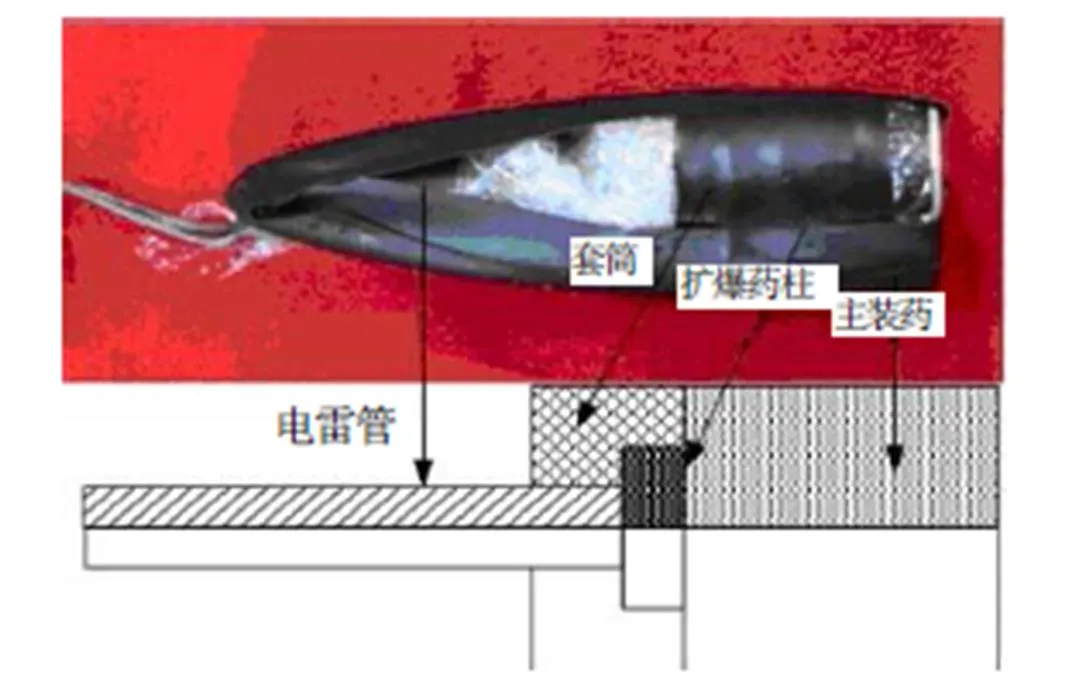
图1 小型组合装药

忽略传爆序列各组件的起爆时差，当8#电雷管、聚黑-14药柱和TNT药柱（密度为1.58g/cm3，初始比内能4.19×106J/kg，CJ爆轰速度为6 930m/s）同时起爆时，如果电雷管和聚黑-14药柱的TNT等效药量分别为1和2，测试用TNT药柱为＇，则组合装药整体的起爆能量可以由下式表示：

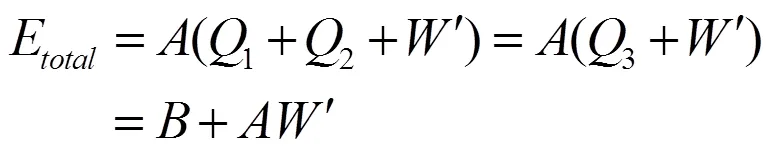
式（12）中：为电雷管和聚黑-14药柱整体起爆释放的能量；为单位质量TNT药柱的爆炸输出能量。8#工业电雷管、聚黑-14药柱分别和8种规格的TNT药柱配合测试以获得等效换算系数和，起爆元件的等效质量为与之商。装药起爆后的总能量由式（11）结合试验测试数据计算得到，其中对于组合装药的平均爆速按TNT药柱爆速近似处理。

3 试验过程及结果

3.1 试验布设

试验在1个尺寸为2.2m×2.2m×2.2m的爆炸水箱中进行，爆炸水箱四周中间位置各设置有1个面积为40cm×40cm的观察窗，用于拍摄气泡的脉动过程，水箱内壁涂有减小冲击波反射效应的吸波材料。

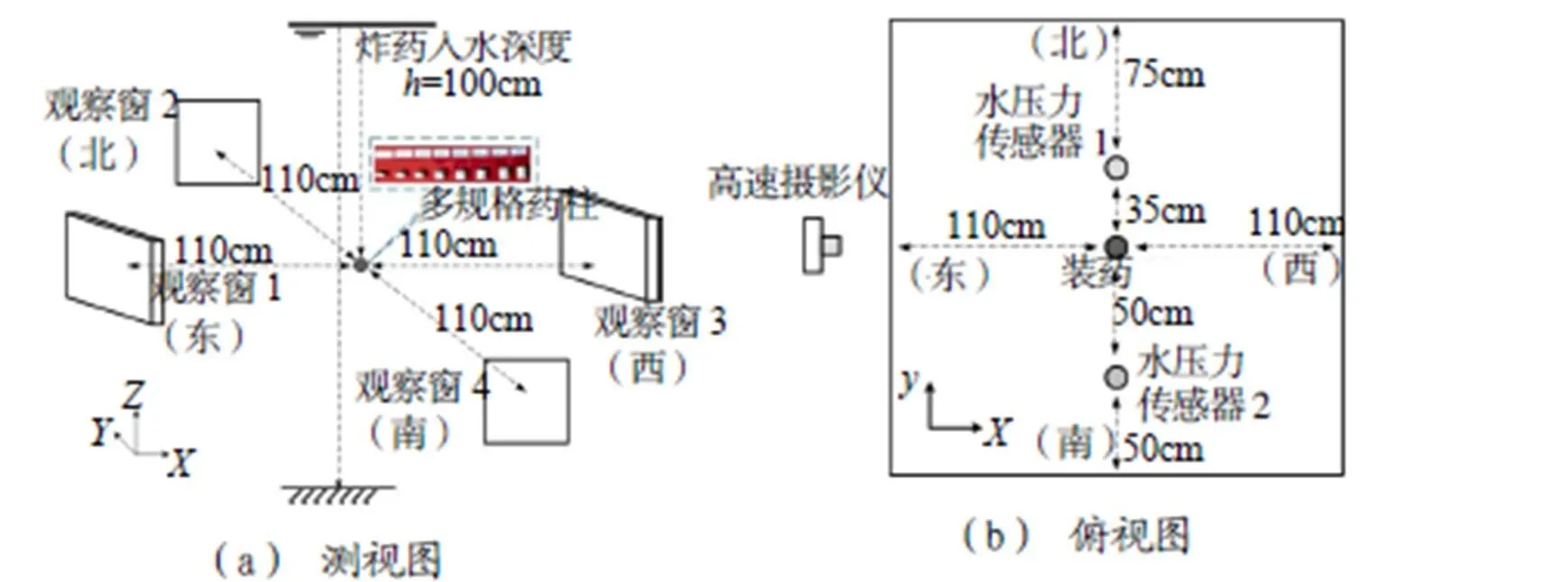
图2 装药及传感器布设

图2为装药及传感器的布设示意图，水箱注水深度为2.05m，装药入水深度1m，布设位置距各观察窗1.1m，2个PCB138A05水压力传感器分别沿组合装药中心水平位置布设在炸药两侧不同距离处（35cm和50cm），以获取不同位置处的冲击波数据。高速摄影设备垂直于主观察窗（观察窗1）布设，以观察气泡周期运动，获取相关数据。

3.2 试验结果

图3（a）和图3（b）分别为起爆元件（8#雷管和聚黑-14药柱）起爆及主装药为4.13gTNT的组合装药起爆后不同时刻的气泡脉动图像。

图3 不同工况下的气泡脉动

图4为主装药为4.96gTNT药柱的组合装药起爆后的压力——时程曲线。图5反映了不同质量TNT药柱的组合装药起爆后的水下爆炸输出能量，根据式(11)和式(12)，采用最小二乘法拟合得到炸药水下爆炸输出能量与TNT药柱质量的关系：

=4 039.29+9 062.31 （13）

其中参数的估值为4 032.29J/g，略小于TNT的理论值4 190J/g，而8#工业电雷管、聚黑-14药柱整体的TNT等效药量3约为2.24g。

表1 试验工况及试验结果

Tab.1 Experiment conditions and results

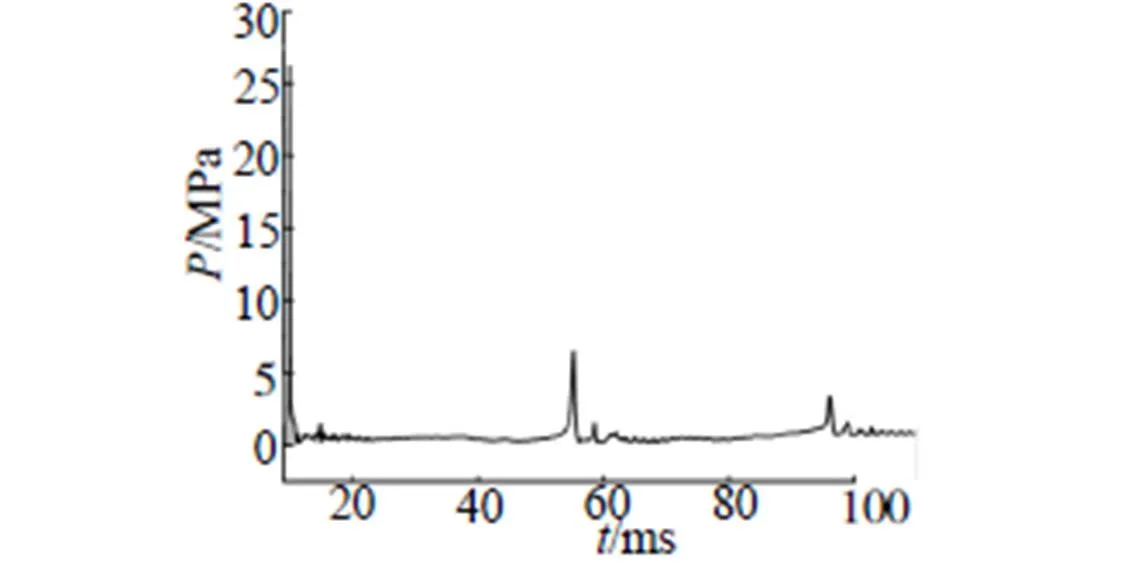
图4 组合装药（4.96gTNT）起爆后的压力测试曲线

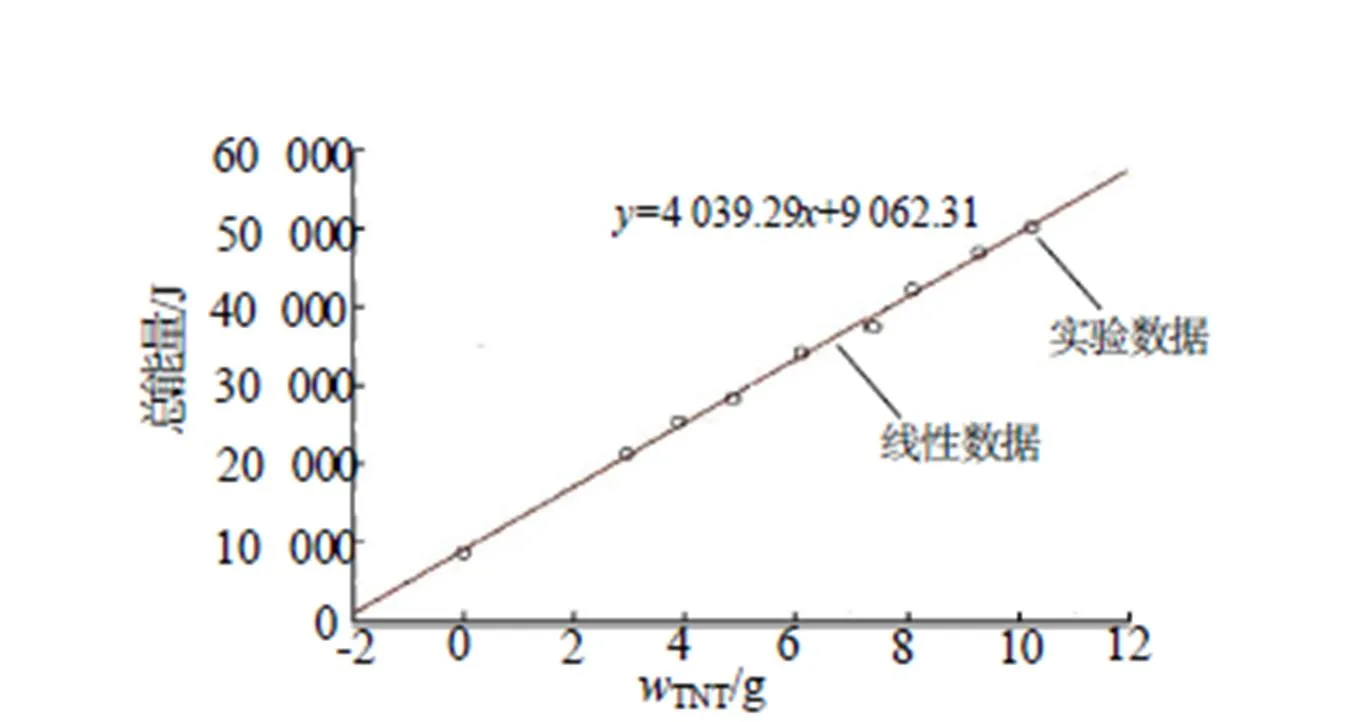
图5 水下爆炸输出能量和TNT药柱质量的关系

为了验证拟合得到的起爆元件TNT等效质量的可靠性，将等效药量3和TNT药柱质量作为组合装药整体的TNT质量，代入式（4）和式（10），计算得到有效比冲能及比气泡能的理论计算值与试验值，见表1。其中关于气泡运动周期和最大半径的计算参考Best拟合的经验公式[13]：

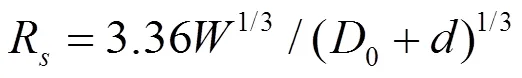
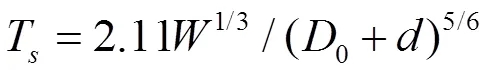
4 试验结果分析

由表1中试验和理论数据的对比可知，基于能量等效原理拟合得到的起爆元件等效质量具有较高的精度。在比气泡能的换算方面，当炸药量较大时（试验8和试验9），试验误差较大，均超过了10%。图6显示了理论和试验气泡半径的对比。由图6可以看出，当组合装药总药量较小时，试验测得的气泡最大半径及一次脉动的周期与Best拟合的经验值十分接近，而随着总药量逐渐增大，气泡最大半径的试验值与经验值仍相差不大，但气泡运动周期试验值与经验值之间的差距逐渐增大。

图6 理论和试验气泡半径时程变化比较

这是因为本文是基于自由场气泡最大半径计算气泡能并对起爆元件进行TNT等效转换，而尽管试验用爆炸水箱内壁考虑了边界面的反射问题，但当炸药量较大时，水箱内壁和自由水面不可避免地会对气泡的周期运动产生一定影响，而这种影响主要产生于气泡一次脉动膨胀后的收缩阶段[14]，因为气泡振荡（上浮，下沉或侧移）主要发生在这一阶段。

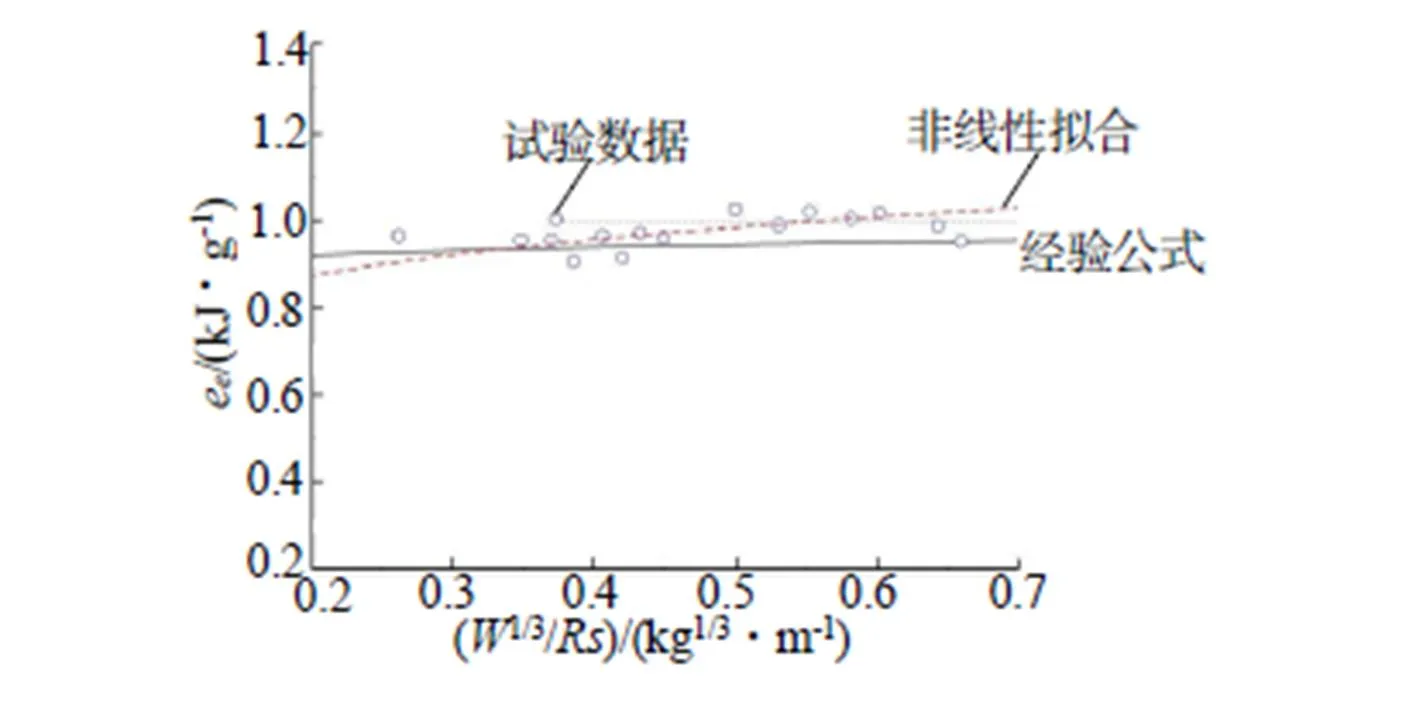
图7 有效比冲能的比较

文献[14]以爆心到边界的距离与气泡最大半径的比值作为判定标准，研究了不同边界条件对气泡脉动运动的影响，发现相对于气泡的脉动周期，气泡半径受边界条件的影响明显更弱，并指出对于近自由面和近刚性壁（或弹性结构边界），当分别满足＞2和＞3时，即可以不考虑边界对于气泡周期运动的影响。而就本文试验而言，除试验9外无论是近自由面还是近壁面均满足＞3，试验结果反映出了边界条件对于气泡最大半径的影响可以忽略不计，因此，就基于气泡最大半径的比气泡能计算而言，试验边界对拟合结果的影响在误差可接受的范围之内，但试验边界条件对气泡周期运动仍产生了一定影响，因为文献[14]仅考虑了单一边界对于气泡运动的影响。

将有效比冲击波能的试验结果和比例距离的关系进行拟合得到：

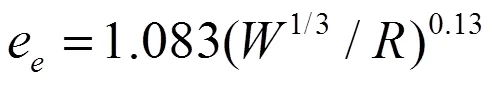
通过图7比较可以看出拟合曲线与经验公式反映出一致的变化趋势，即有效比冲能随比例距离的增大而减小，而其衰减速率增大。

5 结论

对由电雷管和扩爆药柱作为起爆元件的小型TNT药柱进行了水下爆炸测试，基于能量输出的等效原理，拟合得到了起爆元件整体的TNT等效药量。结果表明：（1）当主药量较小时，起爆元件对装药整体能量输出特性的影响十分明显，通过与炸药水下爆炸输出能量计算的理论值相比较，验证了本文提出的等效换算方法的可靠性。（2）针对本文的试验条件，边界条件对气泡最大膨胀半径的影响可以忽略不计，而随着组合装药整体药量增大，一次气泡脉动周期试验值与经验值的差距将会逐渐增大。

[1] 宗智,赵延杰,邹丽,等.水下结构毁伤的数值计算[M].北京:科学出版社,2014．

[2] 杨振,沈晓乐.爆破战斗部水中兵器爆炸威力评定方法研究[J].爆破,2015,32(2):51-54．

[3] 牟金磊,朱锡,李海涛,等.炸药水下爆炸能量输出特性试验研究[J].高压物理学报,2010,24(2):88-92．

[4] 秦健,艾东民,吴成,等.几种炸药水下爆炸能量损失特性分析[J].北京理工大学学报,2015,3(6):566-570.

[5] 王秋实,聂建新,焦清介,等.不同铝氧比六硝基六氮杂异伍兹烷基含铝炸药水下爆炸实验研究[J].兵工学报,2016,37(增刊2):23-28.

[6] 封雪松,田轩,冯博,等.纳米铝粉对炸药水下爆炸能量的影响研究[J].爆破器材,2016,45(3):1-4．

[7] 杨斐,罗一鸣,王建灵,等.铝氧比对DNTF/AP/AI炸药水下能量输出结构的影响[J].火炸药学报,2015,38(2):54-57．

[8] 万晓智,马宏昊,沈兆武,等.高铝含量铝箔膜炸药与铝粉炸药水下爆炸性能的对比分析[J].高压物理学报,2016,30(1): 42-48．

[9] Cole RH.Underwater explosions[M]. New York:Dover Pub Inc,1965．

[10] Kimura E, Qyumi Y. Thermal decomposition of BAMO copoly- mers[J].Propellants, Explosives,Pyrotechnics,1995(20): 322- 326.

[11] 苏华,陈网桦,吴涛,等.炸药水下爆炸冲击波参数的修正[J].火炸药学报,2004,27(3):46-48．

[12] C.F. Hung， P.Y. Hsu， J.J. Hwang-Fuu,et al. Elastic shock response of an air-backed plate to underwater explosion[J]. International Journal of Impact Engineering,2005(31):151-168．

[13] Best J P. The effect of non-spherical collapse on determination of explosion bubble parameters[R].ADA4078761,2002．

[14] 牟金磊,朱锡,张振华.近自由面水下爆炸气泡现象的数值仿真研究[J].舰船科学技术,2008,30(4):113-116．

Equivalent Evaluation of the Initiation Component of Small-sized Composite Charges Based on Underwater Explosion Energy Output

WU Jian-yu1,XIE Xing-bo1,ZHONG Ming-shou1,SONG Ge1,WANG Min1,LI Ying2

（1. College of Field Engineering, Army Engineering University, Nanjing, 210007；2.Naval Academy of Armament, Beijing, 100161）

In order to increase the reliability and accuracy of underwater explosion (UNDEX) test of small-sized composite charges used in model experiment, the underwater explosion parameters of TNT grain initiated by the initiation component composed of electric detonator and auxiliary booster grain were measured. Based on the equivalent of energy output, the TNT equivalent quality of initiation component was obtained. The results indicated that the initiation component will greatly affect the whole energy out when the main charge mass is very small, and the equivalent conversion method is proved to be effective by comparing with the empirical values of the UNDEX energy output. In the existing experimental conditions, the effect of the boundary conditions on the maximum bubble radius can be ignored, while the difference between the experimental and theoretical pulsation cycle will be significantly enlarged.

Underwater explosion；Initiation component；Shock wave energy；Bubble energy；Equivalent conversion

1003-1480（2018）03-0001-05

TJ45+3

A

10.3969/j.issn.1003-1480.2018.03.001

2017-12-04

吴建宇（1992 -），男，博士研究生，主要从事爆炸毁伤效应研究。

国家自然科学基金项目（51339006,51508569）；江苏省自然科学基金项目（Bk20151449）。