生活中的几何问题
文 /王华军

数学来源于生活,又服务于生活.下面以中考题为例,把生活中的几何问题归类如下,供你复习时参考.
一、解释现象
例1某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图1),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间线段最短.
B.两点确定一条直线.
C.垂线段最短.
D.经过直线外一点,有且只有一条直线与这条直线平行.
解析:剩下的银杏叶的周长比原银杏叶的周长要小,实质上就是剪掉的叶片两端点之间,线段的长度小,依据是“两点之间线段最短”.选A.
温馨小提示:“两点之间线段最短”用于缩短路程;“两点确定一条直线”用于“直”但不涉及到“长短”;“垂线段最短”适应于比较线段的大小.

图1
二、平行管道的对接
例2如图2所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°. B.100°. C.80°. D.60°.

图2
解析:两平行直线被第三条直线所截,同旁内角互补,因此,另一侧铺设的角度大小为180°-120°=60°.选D.
温馨小提示:这里应用平行线的性质,解决了铺设平行管道中的对接问题,体现了数学的应用价值.
三、生活中的对称图案
例3如图3,下面四个手机应用图标中,属于中心对称图形的是( )

图3
解析:只有B图形是中心对称图形.选B.
温馨小提示:判断一个图形是否是中心对称图形,关键是看在平面内能否找到一个点,把图形绕着这个点旋转180°,旋转后的图形是否能与原来的图形重合.
四、小巷的宽度
例4如图4,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米. B.1.5米. C.2.2米. D.2.4米.
解析:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,
∴BD2+A′D2=A′B′2,
∴BD2+22=6.25,∴BD2=2.25,
∴BD=1.5(米),
∴CD=BC+BD=0.7+1.5=2.2(米).选C.
温馨小提示:将勾股定理与方程结合是解几何题的常用方法,是数形结合思想的应用.
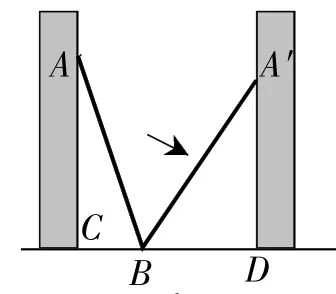
图4
五、景点的位置
例5如图5是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是_____.
解析:如图5,过点A作AD⊥x轴于点D,连接AC.
∵A(400,300),∴OD=400m,AD=300m.
∵AD⊥OD,CB⊥OB,∴∠ODA=∠ABC=90°.
∵AB=300m,BC=400m,由勾股定理得AC=500m.
在△AOD和△ACB中,∵AD=AB,∠ODA=∠ABC,DO=BC,
∴△AOD≌△ACB,∴∠CAB=∠OAD,AO=AC.
∵点B,A,O在一条直线上,∴点C,A,D也在一条直线上,
∴AO=AC=500m,∴CD=AC+AD=800m,∴C点坐标为(400,800).
温馨小提示:将实际问题转化为数学问题是解题的关键.若是解答题,要谨防默认“点C,A,D在一条直线上”而出现的错误.
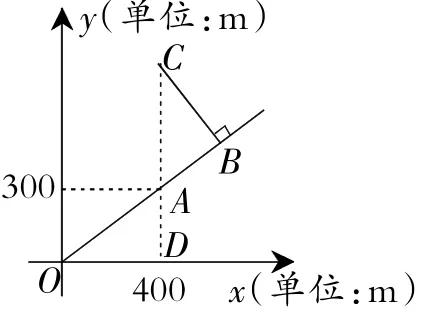
图5
六、工程质量的检验
例6如图6是某斜拉桥的剖面图.BC是桥面,AD是桥墩,设计大桥时工程师要求斜拉的钢绳AB等于AC.大桥建成后,工程技术人员要对大桥质量进行验收,由于桥墩AD很高,无法直接测量钢绳AB,AC的长度.请你用两种不同的方法检验AB,AC的长度是否相等.(检验工具为刻度尺;检验时,人只能在桥面上)
解析:测量一些数据后,可利用全等三角形证明AB=AC.
方法1:用刻度尺测量BD,CD的长度,若BD=CD,又AD⊥BC,所以∠ADB=∠ADC,AD是公共边,则△ABD≌△ACD,∴AB=AC.
方法2:如图6,在∠B的两边任取两点E,P,在∠C的两边取两点F,Q,使BE=CF,BP=CQ,再度量EP和FQ的长度,若EP=FQ,则AB=AC.
理由如下:在△BEP和△CFQ中,BE=CF,BP=CQ,EP=FQ,所以△BEP≌△CFQ,所以∠B=∠C,即AB=AC.
温馨小提示:利用等腰三角形的概念与判定方法,构造全等三角形,解决测量长度问题.
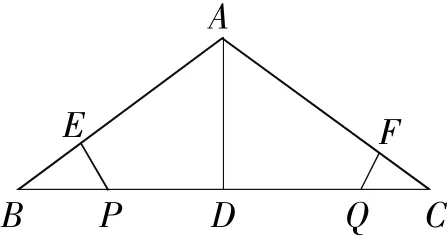
图6
七、行走的路程
例7如图7为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为______m.
解析:已知小敏行走的路程来求小聪行走的路程,就需要求出小聪行走的路程与小敏行走路程的关系.比较两人走的路线,小敏走的路程为AB+AG+GE=1500+(AG+GE)=3100,则AG+GE=1600m,小聪走的路程为BA+AD+DE+EF=3000+(DE+EF).下面关键是要寻找AG+GE与DE+EF的关系,这样就把实际问题转化为数学问题.
连接CG.在正方形ABCD中,∠ADG=∠CDG=45°,AD=CD.
在△ADG和△CDG中,∵AD=CD,∠ADG=∠CDG,DG=DG,
∴△ADG≌△CDG,∴AG=CG.
又∵GE⊥CD,GF⊥BC,∠BCD=90°,
∴四边形GECF是矩形,∴CG=EF.
∵∠CDG=45°,∴DE=GE,
∴小聪走的路程BA+AD+DE+EF=3000+(GE+AG)=3000+1600=4600(m).
温馨小提示:本题比较复杂,经过分解转化,问题得到了简化,即寻找AG+GE与DE+EF的关系,将问题转化为证明两条线段相等,从而找到了解决问题的途径.
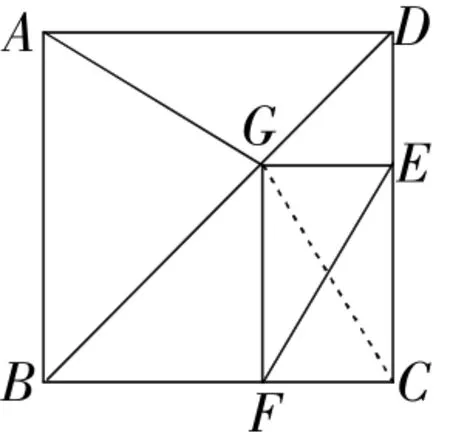
图7
八、几何体的表面积
例8如图8是某几何体的三视图,根据图中数据,求得该几何体的表面积为_____.
解析:由三视图可知,几何体是由圆柱体和圆锥体构成的,
温馨小提示:判断几何体的形状、确定圆锥的底面直径和高是解题的关键.
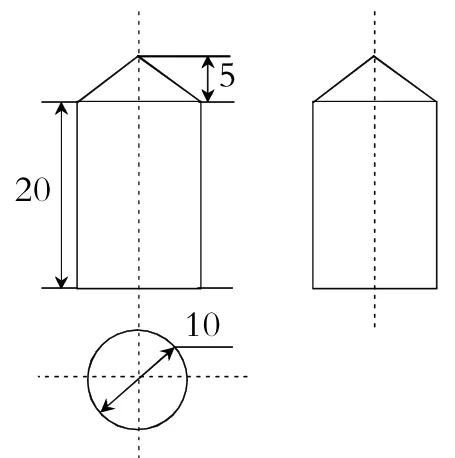
图8
九、求热水器的支架长
例9某太阳能热水器的横截面示意图如图9所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号)
解析:(1)在Rt△CDE中,∠CDE=30°,DE=80cm,
(2)在Rt△OAC中,∠BAC=30°,AC=165cm,
温馨小提示:本题主要考查解直角三角形的应用,将实际问题抽象为数学问题,构造直角三角形求解.
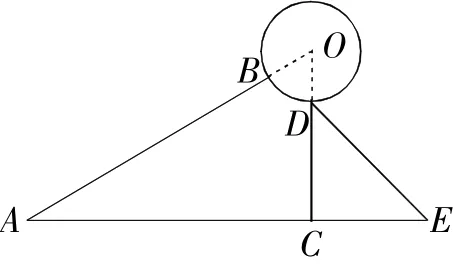
图9

