基于子空间投影的加权DOA算法*

王华奎,陈 峰,王 彪

(1.水声对抗技术重点实验室,广东 湛江 524022;2.江苏科技大学电子信息学院,江苏 镇江 212003)

一直以来,高分辨DOA估计都是阵列信号处理的热点问题,许多专家学者都对此进行了深入研究[1-3]。DOA估计算法大体可以分为以下两类:一类是以常规的CBF(波束形成)和MVDR[4](最小方差无畸变算法)等为代表的传统算法;一类是以MUSIC[5-6](多重子空间分类算法)、ESPRIT(旋转不变子空间算法)为代表的超分辨算法。相比于传统的波束形成算法,超分辨算法拥有更高的分辨率以及更精准的估计性能,但在低信噪比、小快拍条件下,此类算法的估计性能急剧下降甚至失效。为此文献[7-9]对MUSIC算法进行深入研究,文献[7]将加权之后的信号子空间引入传统MUSIC算法之中,充分利用信号子空间的抗噪性,提高了算法在低信噪比、小快拍下的稳健性。文献[8]提出一种利用加权伪噪声投影的MUSIC算法,利用伪噪声子空间的投影对基于噪声子空间投影的MUSIC空间谱进行加权处理,使得算法在小快拍和弱信号条件下的估计性能大幅提升。文献[9]利用峰值处符号的变化提出了一种基于二阶导数的空间谱函数,此方法在小角度差、低信噪比条件下依然可以得到了比较尖锐谱峰,在一定程度上提高了算法的分辨率。

以上这些算法,虽然都在一定程度上提高了算法的性能,但是却都没有充分利用数据矩阵的特征信息。因此,本文提出一种充分利用数据特征信息的加权MUSIC算法。算法首先利用噪声特征值对噪声子空间投影进行加权,然后结合加权子空间投影算法,形成一种新的空间谱算法。此算法既保留了MUSIC算法的高分辨特性,同时引入了信号子空的抗噪性,使得此算法更加适用于低信噪比、小快拍的条件。最后文章对所提算法联合MVDR进行估计,经过计算机仿真实验说明了所提算法的优越性。

1 MUSIC算法信号模型

假设远场波导条件下有k个窄带信号源入射到M个水听器组成的均匀线阵上,其入射角度为θ,θ={θ1,θ2,…θk},每个阵元之间的距离为d,故其阵元接收数据模型如下:

X(t)=A(θ)S(t)+N(t)

(1)

式中,

A(θ)=[a(θ1),a(θ2),…,a(θk)]

(2)

a(θk)=[1,e-j2πdsin(θk)/λ,…,e-j2π(M-1)dsin(θk)/λ]T

(3)

(4)

N(t)=[n1(t),n2(t),…nM(t)]T

(5)

假设每个阵元上的噪声均为零均值的高斯白噪声,且相互独立,接收数据的协方差矩阵用R表示,则R可由下面表达式求得

R=E[X(t)XH(t)]

=E[A(θ)S(t)SH(t)AH(θ)+N(t)NH(t)]

=A(θ)RSSAH(θ)+σ2I

(6)

其中,符号H表示共轭转置运算。由式(6)知,可将R看作是由信号子空间和噪声子空间构成,其表达式:

(7)

其中,ΛS=diag(λ1,λ2,…,λk)是由较大的特征值构成的信号特征值矩阵,ΛN=diag(λk+1,λk+2,…,λM)是由较小的特征值构成的噪声特征值矩阵,在理想的情况下认为λk+1=λk+2=…=λM,但是实际情况下,由于快拍数有限,噪声特征值不可能相等,即λk+1>λk+2>…>λM。US=[e1,e2,…,ek],span(US)=span(A)称为信号子空间,UN=[ek+1,ek+2,…,eM],span(UN)称为噪声子空间。由于span(US)⊥span(UN),所以可以得到span(A)⊥span(UN),故而AHUN=0,R. Schmidt利用这个性质构建了经典MUSIC算法空间谱:

(8)

2 改进算法描述

众所周知,经典MUSIC算法是基于信号相互独立的前提下提出,然而在实际的声场环境下,相干源的存在是一个不可避免的问题,在相干源条件下的MUSIC算法性能急剧下降甚至失效。为获得目标方位角,实现解相干,涌现出了许多解相干方法。其中SSMUSIC、FBSS、MMUSIC是几种最常用的解相干方法,前两种方法都属于降维方法,它们都以损失阵列的有效孔径为代价来实现解相干,相对于MMUSIC来说，估计性能略差。MMUSIC算法具体步骤如下。

假设对式(1)进行变形:

Y=JX(t)*

(9)

其中X*(t)表示为X(t)的复共轭,J为M×M维置换矩阵,其副对角线上元素均为1,其余各元素均为0的矩阵,表达式如下:

(10)

由此可求得样本Y的协方差矩阵Ry=E[Y(t)YH(t)]=JR*J,令RR=R+Ry=R+JR*J,用RR来取代原算法中R进行MUSIC算法运算,便可实现对两个相干源的分辨。MMUSIC实质是FBSS的一种特殊形式,它以本身作为一个子阵进行前后平滑,保证了阵列的有效孔径不会减小,使得算法的分辨率优于FBSS算法。为了进一步提升MUSIC算法的解相干能力,本文提出了一个新的平滑方式：

Rxy=E[X(t)YH(t)]+Jconj(E[X(t)YH(t)])J

(11)

Rxx=E[X(t)XH(t)]+Jconj(E[X(t)YH(t)])J

(12)

Ryy=E[Y(t)YH(t)]+Jconj(E[X(t)YH(t)])J

(13)

=RR+E[X(t)YH(t)]+3Jconj(E[X(t)YH(t)])J

(14)

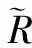
假若式(8)是一个理想的空间谱,理论上是可以进行对任何小角度差的信源进行估计,然而实际中,由于快拍数的有限使得UN并不能获得精确值,因此算法估计性能有所下降,为此文献[10]算法利用噪声特征值的幂数级对相应的UN加以修正:

(15)

(16)

虽然此算法可以在一定程度上提高算法的分辨率,但是却没有给出效果最好时的n值。通过查阅文献和大量的仿真实验,得知0<|n|≤1时,此算法的分辨率较高。n过大,整体空间谱值会变小,可能产生欠估计问题。式(16)的算法在一定程度上提高了算法的分辨率,但是依然没有摆脱MUSIC算法的局限性,算法的实质依旧是利用噪声子空间在导向矢量上的投影来构造空间谱,没有考虑信号子空间的信息,在低信噪比条件下,估计性能依旧不佳。这是由于噪声子空间在小快拍、低信噪比的条件下受影响起伏较大,而信号子空间在此种条件下受影响较小,为此,本文选取一种加权信号子空间的投影方式:

(17)

由上式可得,当m取不同值时,所对应的物理意义不一样,当m=-1时,表示采用主特征值的倒数对信号子空间的投影进行加权,其实质是弱化了最大特征向量的投影,使得其他方向信号的特征向量投影得以加强,从而提高小角度下的信源分辨性能。与之相反,当m=1时,表示采用主特征值对信号子空间的投影进行加权,其实质是放大了最大特征向量的投影,从而使得此方向上的空间谱值更加突出。当m=0时,表示对直接采用信号子空间在A(θ)上的投影,对每个信号的特征向量均用1进行加权。为了获得更加明显的空间谱值,本文选取m=1来构建式(17),然后结合式(16)来构建一种新的空间谱函数

(18)

由式(18)可知,新的空间谱函数是利用功率谱对式(16)的整体加权。式(17)取m=1其物理意义就是信号的功率谱。因此式(17)在m=1可被用来做功率估计。

依据MVDR的本质是在整体功率最小的情况下,让信号处的增益最大,为了让式(18)优势更加明显,稳健性更强,本文使用MVDR空间谱函数和式(18)进行联合估计。为此得到式(19)：

(19)

由上式的物理意义知,相比于式(18)利用式(19)进行DOA估计时信号增益方向将被进一步增强,峰值将会更加尖锐,而旁瓣将会被进一步压制,说明此方法的稳健性更强。仿真实验对算法优越性进行了验证。

3 算法复杂度分析

本文将所提的基于子空间投影加权的加权MUSIC算法式(18)称为算法1、它的联合估计谱式(19)称为算法2,对三种算法复杂度进行分析。

MMUSIC算法复杂度:计算协方差矩阵RR=R+Ry=R+JR*J其运算复杂度为O(L(M2+2M))其中L代表快拍数,计算R复杂度为O(LM2)对其进行特征值分解其运算量为O(M3),故而其总运算量为O(M3+LM2+2LM)。

所提算法2,较之于算法1增加了一个矩阵求逆过程,算法2复杂度增加O(M3),故而算法2的总复杂度可以表示为O(2M3+2LM2+2LM)。

4 仿真实验

4.1 三种算法的对比实验

假设3个等强度的信源入射到12元均匀线阵上,三个信源入射角度分别为0°、30°、60°,其中0°和60°是两个相干源,本文取信噪比为0 dB,快拍数为100、n=1,阵元间距为半波长,进行三种算法空间谱对比实验,其结果如图1所示。从图1中可以看出三种算法均可在波达角方向形成尖锐的谱峰,但是,与算法1相比,算法2谱峰更加尖锐,增益更大,从而说明算法2较之算法1有更好的DOA估计性能,旁瓣压制更低,说明所提的方法拥有更好的鲁棒性。而MMUSIC算法相比于另外两种算法增益较小,说明MMUSIC在无论是相干源的估计还是独立信号的估计上,估计性能整体弱于另外两种算法。

4.2 三种算法的成功率分析

实验条件:3个等强度的信源入射到12元均匀线阵上,三个信源入射角度分别为0°、30°、60°,其中0°和60°是两个相干源,本文取信噪比从-10 dB按2 dB的间隔增加至10 dB,快拍数为100、n=1,阵元间距为半波长,进行100次独立计算机仿真实验,当偏差在1°内认定算法成功,得到三种算法在不同信噪比下的成功率,其结果如图2所示。从图2中可以得出,三种算法在信噪比等于-10 dB时,成功率都为0,但是随着信噪比的提升,三种算法的成功概率也随之提升,但是在除-10 dB外的任何一个信噪比条件下,算法2的成功率均高于其他两种算法。由此说明算法2性能最优、算法1性能次之,侧面说明所提两种算法更加适用于低信噪比条件下。

保持上述实验条件不变,取快拍数从10按20的间隔增加至200,设置信噪比为0 dB进行100次独立计算机仿真实验,其结果如图3所示。从图3可以得出,在小快拍条件下三种算法的成功率都随着快拍数的增加而增加,在快拍数200时三种算法成功率大致相同。但是在其他快拍数时,三种算法中算法2的成功率最高,MMUSIC算法成功率最低,说明所提两种算法更加适用于小快拍的条件下。

接下来分析阵元数对三种算法的影响,取快拍数为100,信噪比为0 dB,阵元数由4个每次增加2个阵元一直增加到16个阵元,其他实验条件保持不变,对其进行分析,其结果如图4所示。由图4可知,随着阵元数目的增加,三种算法的成功率也随之增加,但是明显可知,算法2的成功率明显高于MMUSIC算法,说明算法2性能是优于MMUSIC,从而说明所提两种算法有一定优越性。

4.3 三种算法的偏差分析

实验条件:3个等强度的信源入射到12元均匀线阵上,三个信源入射角度分辨为0°、30°、60°,其中0°和60°是两个相干源,取信噪比从-10 dB按2 dB的间隔增加到0 dB,快拍数为100、n=1,阵元间距为半波长,进行100次独立计算机仿真实验,其结果如表1所示。由表1可知三种算法的标准差都随着信噪比的增大而减小,其中算法2在三种算法中标准差是最小的,MMUSIC是最大的,说明所提两种算法优于MMUSIC。

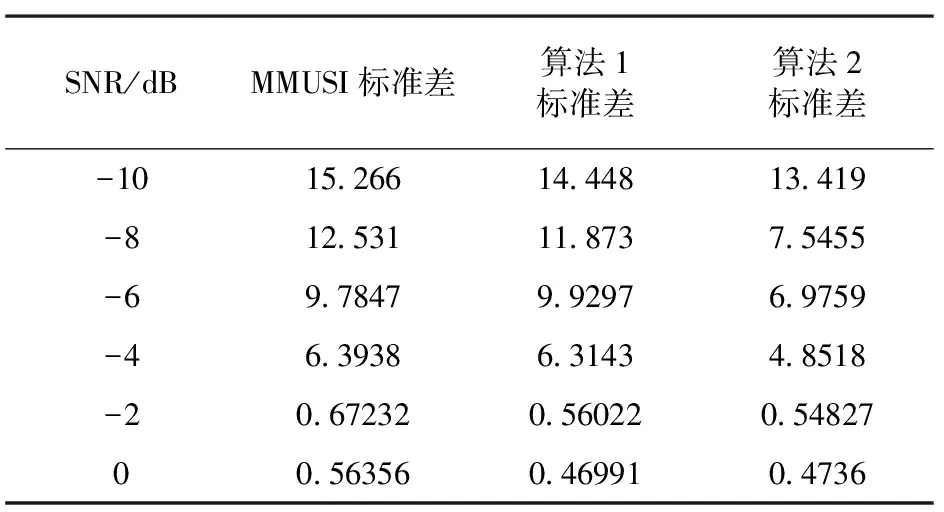
表1 三种算法在不同信噪比下的标准差

保持上述条件不变,将信噪比设置为0 dB,快拍数由120按20的间隔增加到220,其结果如表2所示。

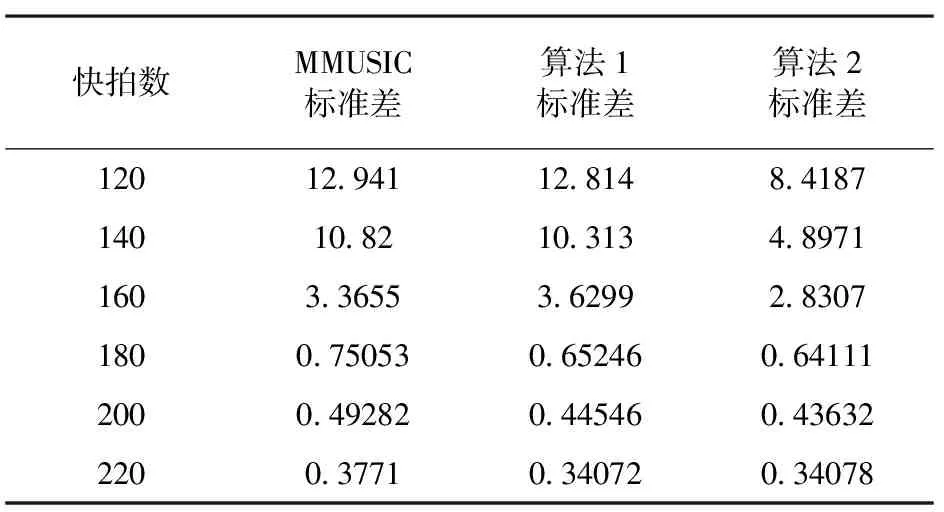
表2 三种算法在不同快拍下的标准差

4.4 三种算法的复杂度分析

假设M=12,快拍数L从1开始每次增加50至301时,三种算法复杂度其复杂如图5所示。从图中可以算法1和算法2运算量相当,随着快拍数的增加算法1和算法2的计算量间的差值将会越来越大。

假设快拍数L=100,阵元数由8变化到20时,三种算法的运算量如图6所示,算法1和算法2运算量相当,对比图6和图5可知,阵元数对计算量的大小是起决定性作用,因为阵元数和复杂度是呈立方关系。虽然本文所提的两种算法的复杂度都随着快拍数和阵元数的增加而增加,但是结合图3、4、5、6可知在阵元数14,快拍数140时,算法1、2性能远高于MMUSIC,而此时本文所提两种算法的复杂度和MMUSIC算法相当。侧面反映了相较于MMUSIC算法,本文所提算法在阵元14、快拍140时能取得最优工作状态。

5 结束语

为了解决传统的MUSIC算法在小快拍、低信噪比的条件下估计性能急剧恶化的问题,本文利用噪声所对应的特征值对噪声子空间进行加权,并将利用主特征值加权信号子空投影和加权后的噪声子空间投影进行结合,构造一种新的空间谱函数,利用MVDR算法对信号有最大增益的特点,对所提算法与MVDR空间谱进行联合DOA估计。为了使算法能够适用于相干源条件下,进而提出一种新的解相干方法,将这种解相干方式与所提的两种算法相结合,有助于提高解相干性能。最后通过计算机仿真实验证明:本文所提两种算法信噪比在-10 dB至4 dB时,性能是优于MMUSIC; 本文所提两种算法阵元数在6至16时,性能是优于MMUSIC。