邻域粗糙集属性约简方法研究

傅 凡，李京政，窦慧莉

（1.江苏省光电子技术中心江苏镇江212000；2.江苏科技大学计算机学院，江苏镇江212003）

经典Pawlak粗糙集模型是建立在等价关系基础上的，适用于处理离散型数据，不适用于直接处理现实中广泛存在的数值型数据，而将数值型数据离散化会导致数据信息的丢失。鉴于此，众多学者提出了多种粗糙集拓展模型[2-6]，例如模糊粗糙集，邻域粗糙集等，其中，邻域粗糙集从使用距离构建邻域的角度出发，其直观简洁的形式以及广泛的应用范围得到了很多学者的关注。

在粗糙集的研究进程中，属性约简[7-13]一直是重要研究内容。所谓属性约简，就是依据粗糙集理论中的某种评价函数设置一个约束条件，使得删除数据中的无关/冗余属性后能够满足这一约束，其目的是简化后续问题处理、加速问题求解或提升学习模型的泛化性能。目前在粗糙集理论中常用的评价函数有近似质量[14]、条件熵、近似分布[15]等，约束条件一般有保持度量不变或使得度量指标的变化在给定阈值范围内。可以知道，基于一种评价函数的属性约简求解出的属性子集可以保证对应的度量指标在约束条件内。从多准则，多视角考虑，评价函数的多样性会对约简结果产生的影响也是研究的主要问题，基于一种评价函数的属性约简求解出的属性子集是否能满足其它度量指标的约束条件，这也为考虑多个评价函数的属性约简提供一个新的方向。

1 邻域粗糙集与邻域分类器

在邻域粗糙集中，一个决策系统可以表示为二元组DS=＜U，AT∪D＞，其中U是非空有限的样本集合，AT是所有条件属性集合，D={d}表示决策属性的合集且AT∩D=ϕ。∀xi∈U，d（xi）是样本xi的类别标记。邻域是通过给定半径考察样本的邻居。不妨假设M=（rij）n×n为论域上的距离矩阵，rij表示样本xi与xj之间的某一种距离度量，给定参数δ∈[0，1]，∀xi∈U，xi的邻域半径为：

δA（xi）表示在样本xi邻域半径内的所有样本。

定义1 令DS=＜U，AT∪{d}＞为一决策系统，∀A⊆AT，根据属性集合A可以得到所有样本之间的距离矩阵，∀xi∈U，∀X⊆U，X的邻域下近似集与上近似集分别定义如下：

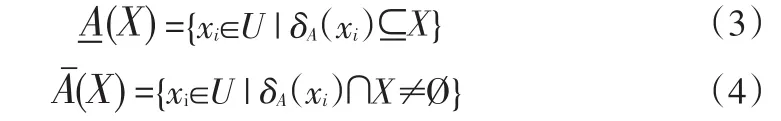
定义2给定一个决策系统DS，∀A⊆AT，∀X⊆U，X相对于A的近似质量为：

其中|X|表示集合X的基数。

在邻域粗糙集的基础上，文献[16]设计出邻域分类器进行分类学习研究，算法1给出了邻域分类器的详细流程。

算法1：邻域分类器

输入：决策系统DS，待预测样本xi，邻域半径参数δ。

输出：样本的预测类别标记PAT(xi)。

步骤1：∀xj∈U，计算δAT(xi)；

步骤 2：∀Xp⊆U/IND({d})，计算Pr(Xp,δAT(xi))=；

步 骤 3：Xq=arg max{Pr(Xp,δAT(xi))| ∀Xp∈U/IND({d})}；

步骤4：PAT(xi)=q，输出ρAT(xi)。

利用邻域分类器，相应的，文献[16]进一步给出了邻域决策错误率的概念，以下是邻域决策错误率的形式化定义。

定义3令DS为一决策系统，决策系统的邻域决策错误率为：

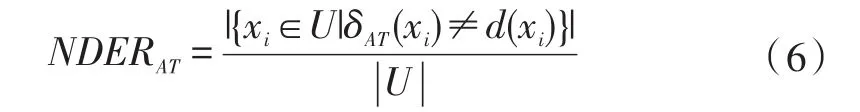
显然，这是一种留一验证方法。从分类学习的视角来看，邻域决策错误率越低，表明分类性能越好。

2 属性约简

定义4给定一决策系统DS，∀A⊆AT，A被当作约简当且仅当f（A，D）=f（AT，D）且∀B⊂A，f（B，D）≠f（AT，D）。

定义4所示的属性约简定义是一个能够保持决策系统中某种度量不发生变化的最小属性子集，其中，f（A，D）表示利用属性集合A的评价函数，以此求得在属性子集上的某种度量指标，这种度量指标可以是近似质量，邻域决策错误率等。进一步考察属性的重要度，∀B∈AT且对于任意的a∈AT-B，如果f（B∪{a}，D）=f（B，D），那么就表明属性a对于计算某种度量没有带来任何贡献，a是冗余的；如果f（B∪{a}，D）≠f（B，D），那么就表示加入属性a后对于计算这种度量产生了影响。可构建如下所示的属性重要度：

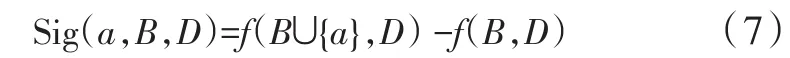
根据上述属性重要度，算法2构建了一个启发式求解属性约简的过程，其目标是获得以定义4为依据的约简。

算法2：启发式算法

输入：邻域决策系统DS=＜U,AT∪D＞。

输出：约简red。

步骤1：令red←Ø；

步骤2：若f(red,D)≠f(AT,D)，则执行以下循环，否则执行步骤3；

(1)∀ai∈AT-red，计算 Sig(ai,red,D)；

(2)选择aj，满足 Sig(aj,red,D)=max{Sig(ai,red,D)|∀ai∈AT-red}，令red=red∪{aj}，返回步骤 2；

(3)计算f(red,D)；

步骤3输出red。

3 实验分析

利用算法2，在求解属性约简的过程中使用了近似质量与邻域决策错误率两种度量准则，分别记为近似质量约简（AQR），邻域决策错误率约简（NDERR）。实验中选取了6组UCI数据集，表1列出了它们的基本信息。使用欧氏距离构造样本之间的距离矩阵，邻域半径参数δ分别设定为0.1、0.2、0.3。在此基础上进行了2组实验，分别比较了利用算法AQR与NDERR求得的近似质量和邻域决策错误率。

表1 实验数据的基本信息

表2列出了利用近似质量约简与邻域决策错误率约简求得的近似质量的对比；表3列出了利用近似质量约简与邻域决策错误率约简求得的邻域决策错误率的对比。

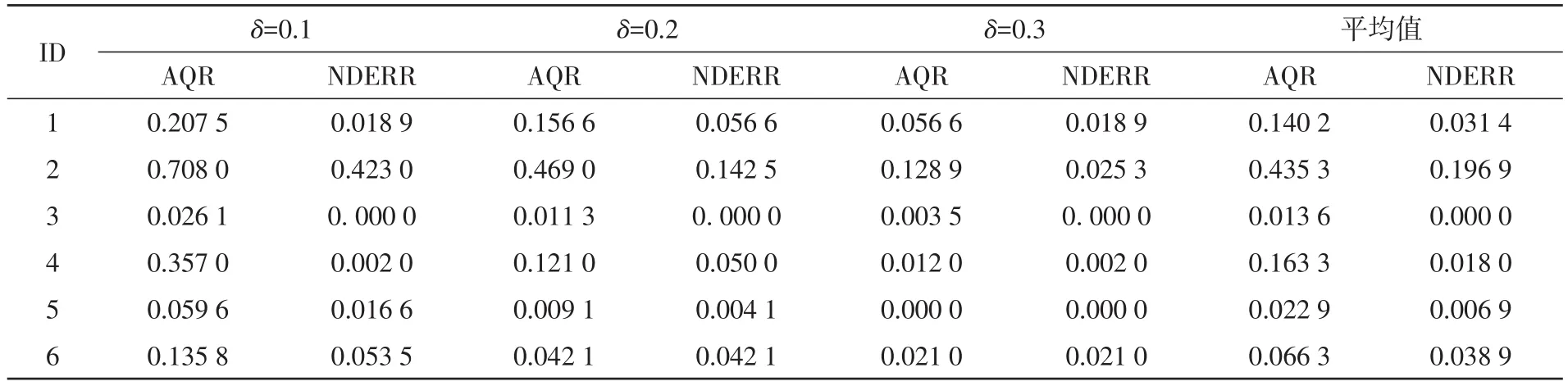
表2 两种约简在近似质量的对比

观察表2与表3可以得到如下结论，在大多数数据集上，由近似质量约简求得的近似质量都要高于由邻域决策错误率约简求得的近似质量，平均要高0.09左右。相应的，由邻域决策错误率约简求得的邻域决策错误率要低于由近似质量约简求得的邻域决策错误率，平均要低0.03左右，除了在数据Diabetic Retinopathy Debrecen上两者相等以外。也就是说，近似质量约简并不能保证约简结果在邻域决策错误率上能够满足约束条件，邻域决策错误率约简也不能保证约简结果在近似质量上能够满足约束条件。

4 结 论

在邻域粗糙集上考虑基于一种评价函数的属性约简结果可以满足相应度量指标的约束条件，不能够保证在其他度量指标的约束条件。一方面，我们证实了传统属性约简的有效性；另一方面，由于基于一种评价函数的属性约简在度量指标的单一性，考虑多个评价函数的属性约简方法也成为一个新的研究方向。