圆端形钢管混凝土柱设计方法对比分析
吴启恂 林泽宗 郑艳莲 陈昭南 王志滨
(福州大学土木工程学院 福建福州 350116)
1 概述
钢管混凝土构件已被大量应用于建筑结构和桥梁结构中。与钢筋混凝土结构、钢结构相比,该类结构具有承载力高、质量轻、延性好、工期短等特点。钢管混凝土构件的截面形式,主要包括圆形、矩形、椭圆形和圆端形(图1),圆端形钢管混凝土具有较大的横向刚度,适合用作桥墩。
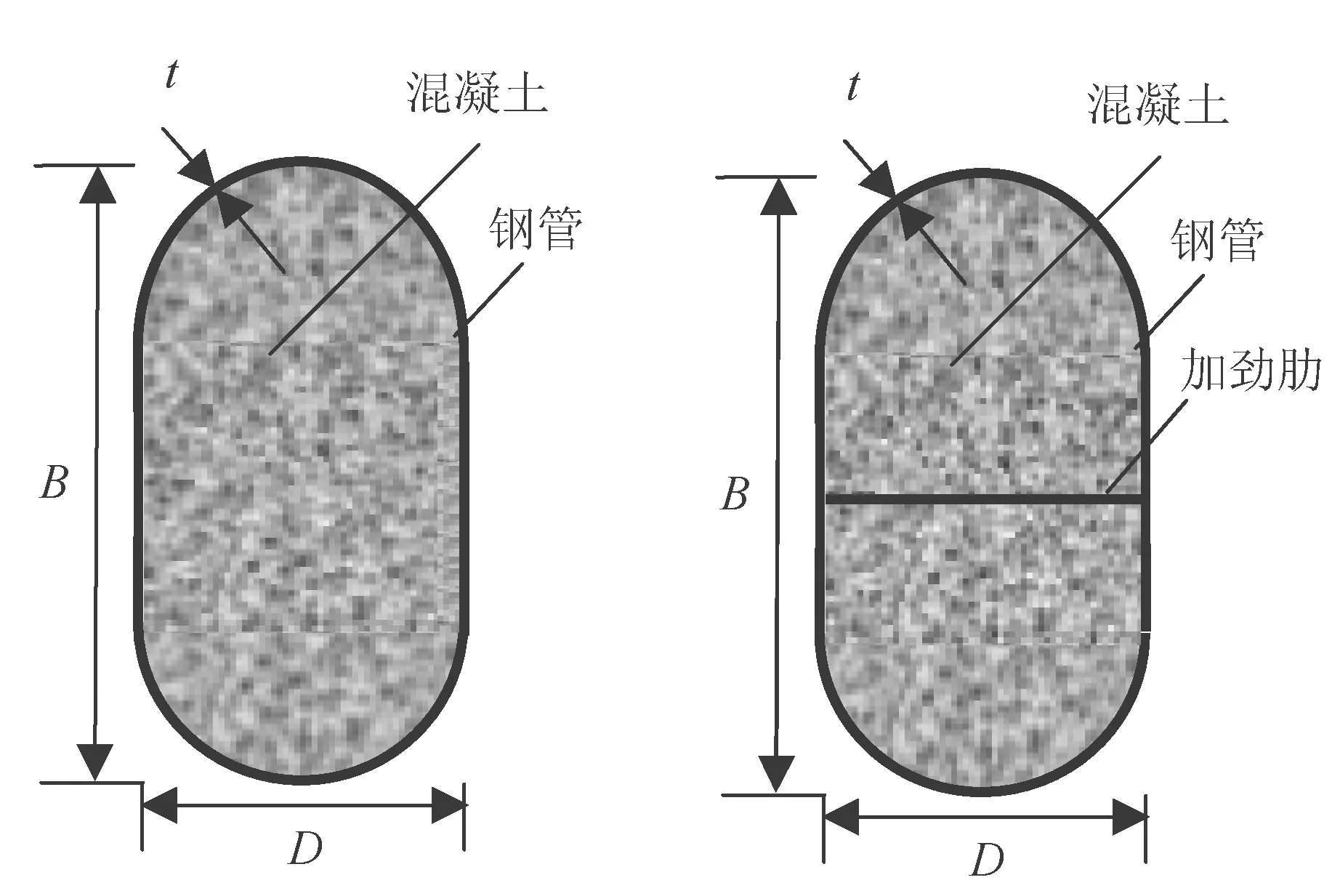
(a) (b)图1 构件截面尺寸图
圆端形截面和椭圆形截面较为相似,但是和圆端形钢管混凝土柱力学性能相关的研究仍不多见。文献[1]通过17根圆端形钢管混凝土轴压短柱的试验,研究高宽比、含钢率、构造措施对力学性能的影响。其研究表明,圆端形钢管对核心混凝土的约束效果和矩形钢管相似,矩形钢管混凝土轴压短柱的设计公式可用于预测圆端形钢管混凝土轴压短柱的承载力。文献[2]进行了10根圆端形钢管混凝土轴压短柱试验,并开展了参数分析。基于有限元模型,文献[3]开展了圆端形钢管混凝土偏压构件的工作机理分析,分析表明钢管的约束作用主要集中在圆弧段。文献[4]和文献[5]进行了15根圆端形钢管混凝土柱的偏压试验,并进行机理分析和参数分析。
到目前为止,现有的规范中并未建议圆端形钢管混凝土柱承载力的简化设计公式。考虑到圆端形钢管的约束作用和矩形钢管、椭圆形钢管较为接近,本文基于现有的圆端形钢管混凝土柱试验结果,验证现有规范[6-9]中的矩形钢管混凝土柱和椭圆形钢管混凝土柱承载力简化设计公式的预测精度,以及验证相关研究文献[2]、[5]中建议的圆端形钢管混凝土承载力简化设计公式的预测精度。以期达到服务工程实践的目的。
2 设计公式介绍和对比
2.1 轴心受压构件
(1)DBJ/T13-51[6]建议了如下矩形钢管混凝土短柱承载力计算公式:
N=fscyAsc+fsyAs,s
(1)
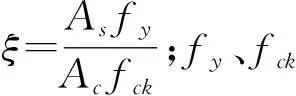
(2)CECS 159[7]也建议了如下矩形钢管混凝土短柱的承载力计算公式:
N=fyAs+fcyAc
(2)
(3)GB 50936[8]建议了如下椭圆形钢管混凝土短柱承载力计算公式:
N=(1.212+Bθ+Cθ2)fck·Asc
(3)
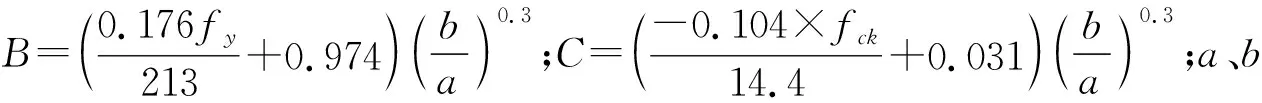
(4)EC4[9]建议了如下矩形钢管混凝土短柱承载力计算公式:
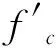
(5)文献[2]中建议了如下圆端形钢管混凝土短柱承载力计算公式:
N=Ac·fck·[1+(0.8+0.9D/B)·ξ]
(5)
2.2 偏心受压构件
(1)DBJ/T13-51[6]建议了如下矩形钢管混凝土偏压构件稳定承载力计算公式:
当N/Nu≥2φ2η0时:
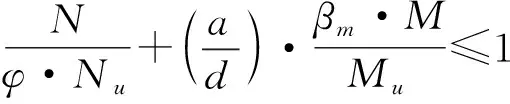
当N/Nu<2φ3η0时:
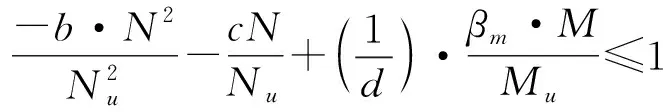
其中,βm为等效弯矩系数;φ为轴心受压构件稳定系数;
η0=0.1+0.13·ξ-0.81;NE为欧拉临界力,NE=π2·Esc·Asc/λ2;Esc为组合弹性模量;λ为钢管混凝土柱的长细比。
(2)CECS 159[7]建议了如下矩形钢管混凝土偏压构件的稳定承载力计算公式:
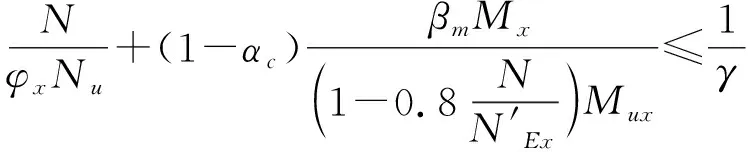
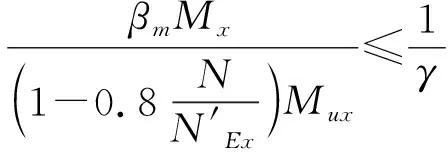
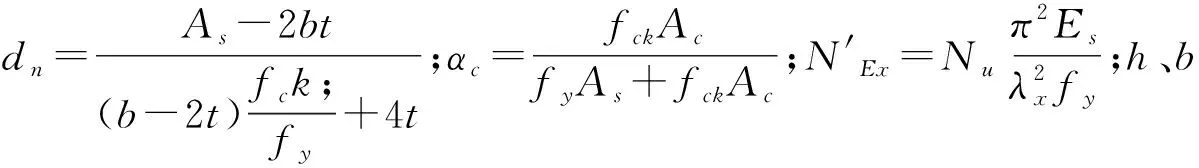
(3)GB 50936[8]建议了如下椭圆形钢管混凝土偏压构件的承载力设计公式:
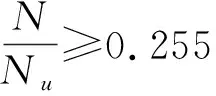
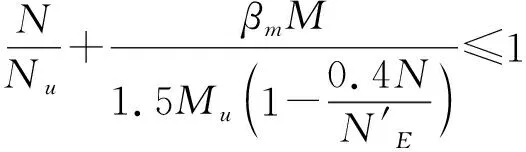
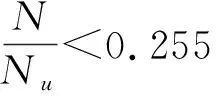
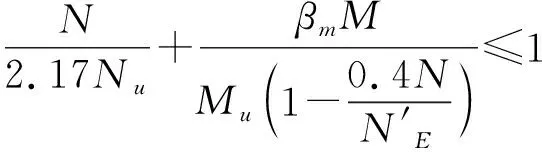
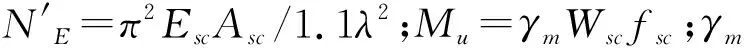
(4)EC4[9]建议了如下钢管混凝土偏压构件的3段相关方程:
Np≤N≤Ncr时:
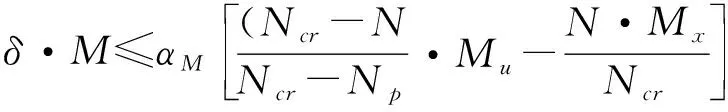
0.5Np≤N≤Np时:
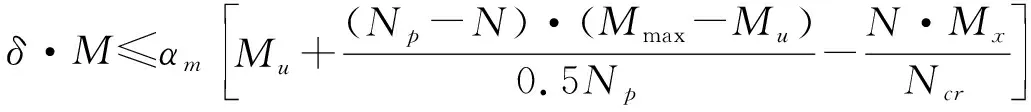
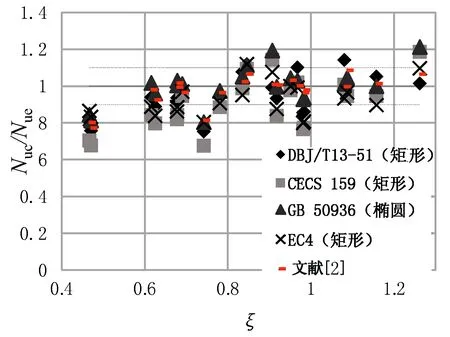
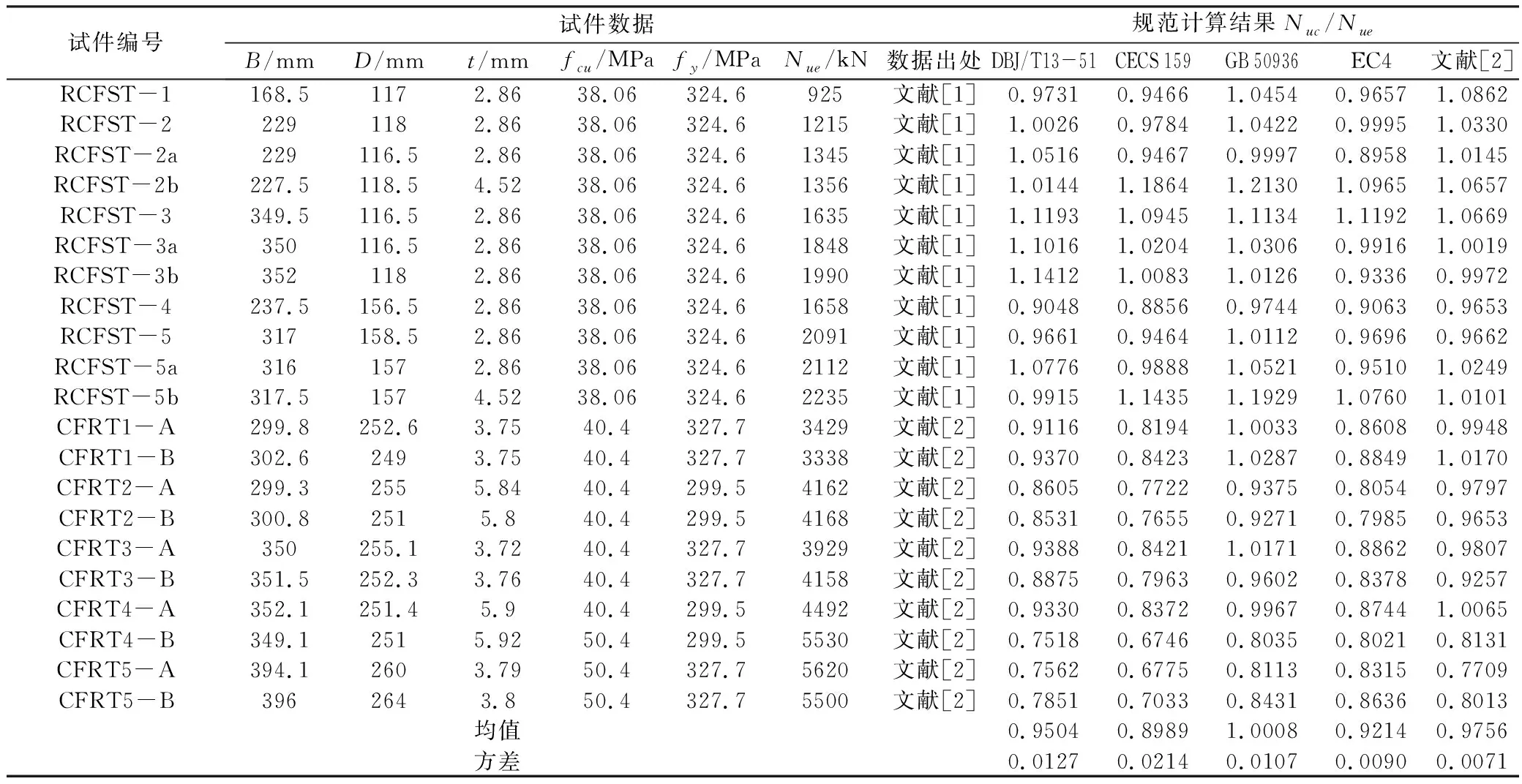
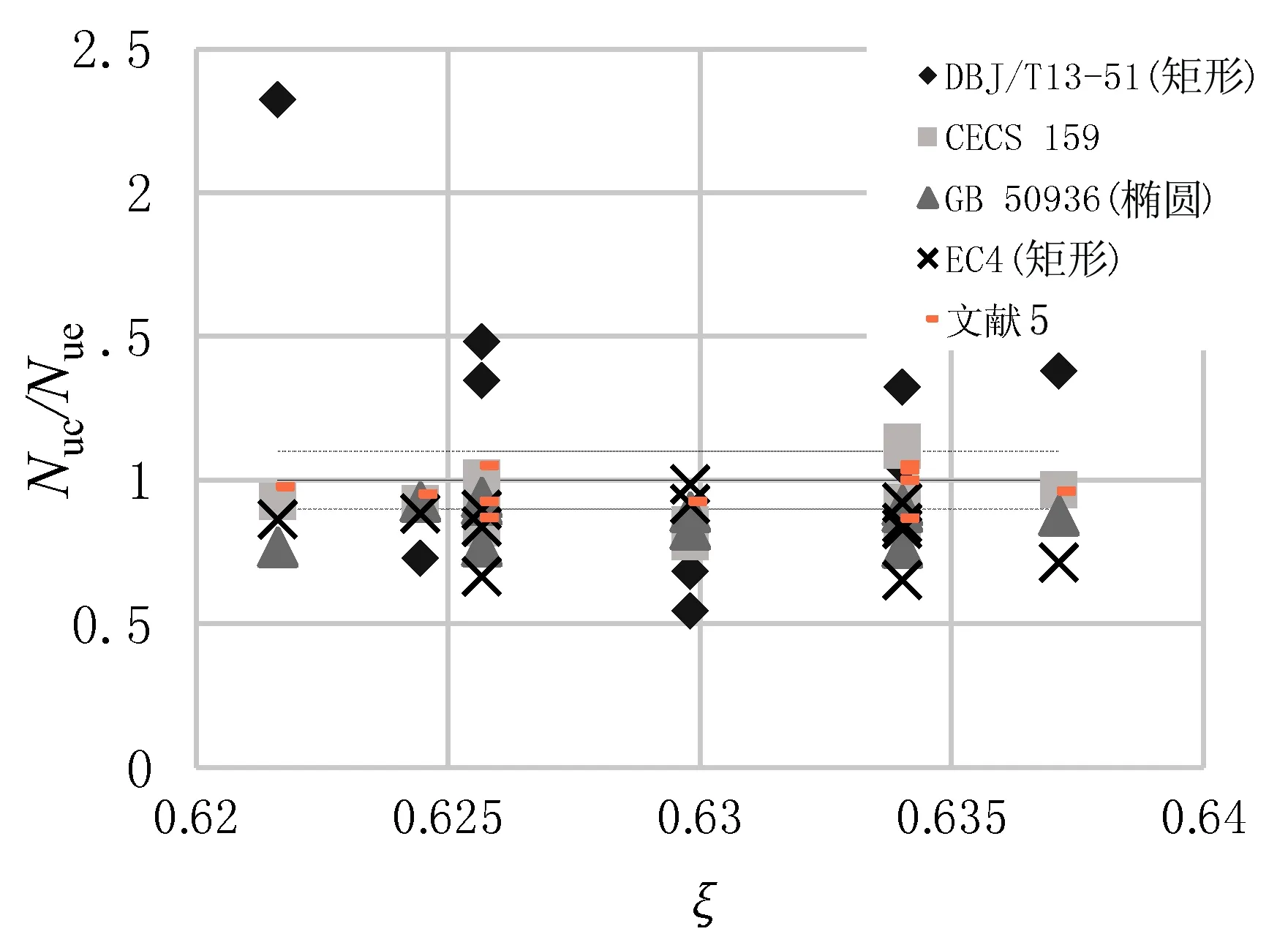
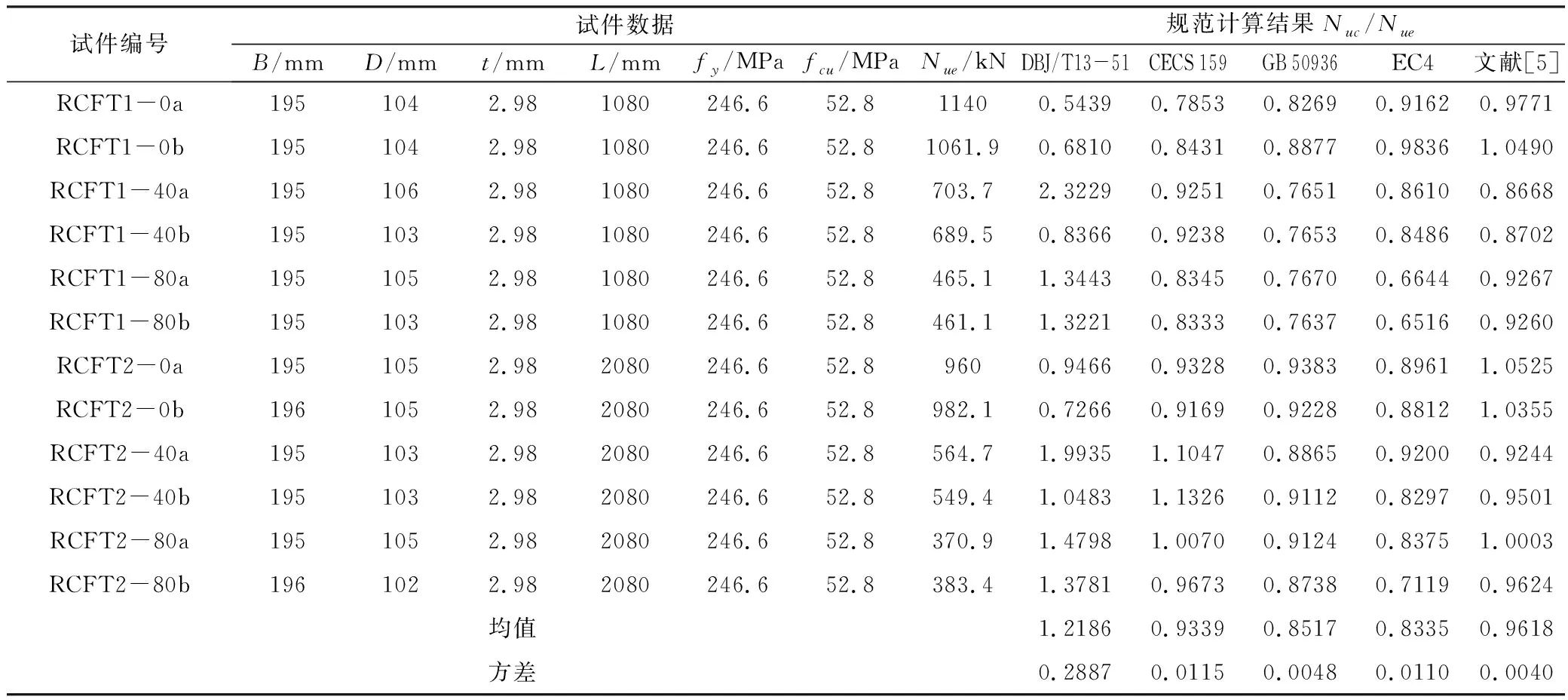
0 (5)文献[5]建议了如下圆端形钢管混凝土偏压构件的承载力设计公式: 表1中给出了本文收集的21根圆端形钢管混凝土柱轴压试件数据[1-2]。表中,B为构件截面高度,D为构件截面宽度,t为钢管壁厚,L为构件长度,fcu为实测混凝土立方体抗压强度,fy为钢材屈服强度,Nue为构件破坏时实测承载力,Nuc为简化计算公式预测的承载力。其中试件RCFST-2a、RCFST-2b、RCFST-3a、RCFST-5a、RCFST-5b中设置了1道纵向加劲肋(图1b),试件RCFST-3b中设置了2道纵向加劲肋。 采用以上5种轴压计算模型预测的圆端形钢管混凝土构件的承载力和实测值的比值Nuc/Nue均列于表1和图2中,同时还给出了Nuc/Nue的均值和方差。可发现DBJ/T13-51[6]、CECS 159[7]和EC4[9]均低估了圆端形钢管混凝土构件的承载力;GB 50936[8]和文献[2]的预测精度最高,且文献[2]的预测结果偏于安全。 图2 轴压短柱承载力计算值与实测值对比表1 试件数据及计算结果表 试件编号试件数据规范计算结果Nuc/NueB/mmD/mmt/mmfcu/MPafy/MPaNue/kN数据出处DBJ/T13-51CECS 159GB 50936EC4文献[2]RCFST-1168.51172.8638.06324.6925文献[1]0.97310.94661.04540.96571.0862 RCFST-22291182.8638.06324.61215文献[1]1.00260.97841.04220.99951.0330 RCFST-2a229116.52.8638.06324.61345文献[1]1.05160.94670.99970.89581.0145 RCFST-2b227.5118.54.5238.06324.61356文献[1]1.01441.18641.21301.09651.0657 RCFST-3349.5116.52.8638.06324.61635文献[1]1.11931.09451.11341.11921.0669 RCFST-3a350116.52.8638.06324.61848文献[1]1.10161.02041.03060.99161.0019 RCFST-3b3521182.8638.06324.61990文献[1]1.14121.00831.01260.93360.9972 RCFST-4237.5156.52.8638.06324.61658文献[1]0.90480.88560.97440.90630.9653 RCFST-5317158.52.8638.06324.62091文献[1]0.96610.94641.01120.96960.9662 RCFST-5a3161572.8638.06324.62112文献[1]1.07760.98881.05210.95101.0249 RCFST-5b317.51574.5238.06324.62235文献[1]0.99151.14351.19291.07601.0101 CFRT1-A299.8252.63.7540.4327.73429文献[2]0.91160.81941.00330.86080.9948 CFRT1-B302.62493.7540.4327.73338文献[2]0.93700.84231.02870.88491.0170 CFRT2-A299.32555.8440.4299.54162文献[2]0.86050.77220.93750.80540.9797 CFRT2-B300.82515.840.4299.54168文献[2]0.85310.76550.92710.79850.9653 CFRT3-A350255.13.7240.4327.73929文献[2]0.93880.84211.01710.88620.9807 CFRT3-B351.5252.33.7640.4327.74158文献[2]0.88750.79630.96020.83780.9257 CFRT4-A352.1251.45.940.4299.54492文献[2]0.93300.83720.99670.87441.0065 CFRT4-B349.12515.9250.4299.55530文献[2]0.75180.67460.80350.80210.8131 CFRT5-A394.12603.7950.4327.75620文献[2]0.75620.67750.81130.83150.7709 CFRT5-B3962643.850.4327.75500文献[2]0.78510.70330.84310.86360.8013 均值0.95040.89891.00080.92140.9756方差0.01270.02140.01070.00900.0071 文献[5]进行了12根圆端形钢管混凝土柱的偏压试验,其详细参数列于表2中。 采用以上5种偏压计算模型预测的承载力和实测值的比值Nuc/Nue均列于表2和图3中,同时还给出了Nuc/Nue的均值和方差。可发现GB 50936[8]和EC4[9]低估了圆端形钢管混凝土构件的承载力;DBJ/T13-51[6]则高估了圆端形钢管混凝土构件的承载力;CECS 159[7]和文献[5]的预测精度最高。 图3偏压柱承载力计算值与实测值对比 表2 试件数据及计算结果表[5] (1)对于圆端形钢管混凝土轴压短柱,DBJ/T13-51[6]、CECS 159[7]和EC4[9]均低估了圆端形钢管混凝土构件的承载力;GB 50936[8]的预测精度最高。GB 50936[8]和文献[2]建议的简化公式的计算结果与实测承载力吻合最好。 (2)对于圆端形钢管混凝土偏压柱,GB 50936[8]和EC4[9]低估了圆端形钢管混凝土构件的承载力;DBJ/T13-51[6]则高估了圆端形钢管混凝土构件的承载力;CECS 159[7]和文献[5]的预测精度最高。 建议在此结论基础上进一步开展机理分析和参数分析,优化设计公式,进一步提高圆端形钢管混凝土柱承载力的预测精度。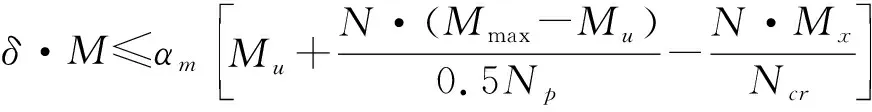
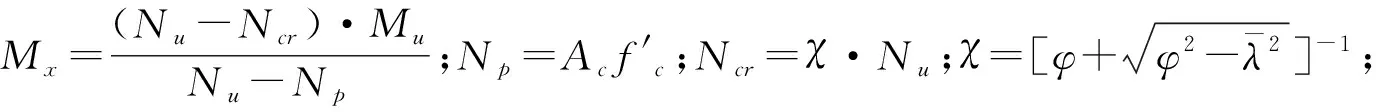
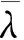
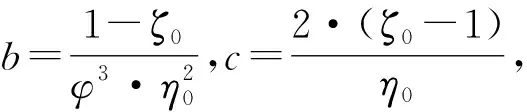
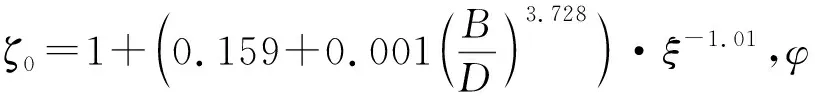
3 简化模型验证
3.1 轴压承载力
3.2 偏压承载力
4 结论

