高中文科学生数学计算能力提升的教学策略
张 玲
(广东省广州市第四十四中学,广东 广州)
数学运算能力是三大数学能力的基础,纵观全国各地的高考试卷,涉及运算的题目所占比重不小,说明这个能力也是高考考查的重点。但笔者在近几年的高中数学文科班教学中发现:高中文科学生的数学运算能力存在着很大的问题,在分析问题时,都以为是“粗心”导致的计算错误,从而让“粗心”掩盖了所有问题。
国内多项研究发现,影响高中生数学运算能力发展的因素主要有以下几点:(1)基础知识和基本方法因素,学生对基础知识和基本方法的掌握影响着运算能力的发展;(2)数学思想方法因素,数学思想方法在数学运算中有着重要作用,学生在学习中对数学思想方法的忽视影响着数学运算能力的发展;(3)学生数学学习的非智力因素,学生的数学学习习惯、学生的意志品质和心理素质影响运算能力的发展;(4)教师教学因素,教师传统的教学观念和陈旧的教学方式影响着数学运算能力的发展。
近几年高考全国卷对文科学生计算能力的要求难度加大。比如:(2015高考新课标全国卷Ⅰ,文6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有 ( B)
A.14斛 B.22斛 C.36斛 D.66斛

解析:设圆锥底面半径为r,
因为米堆底部弧长为8尺,
所以米堆的体积为
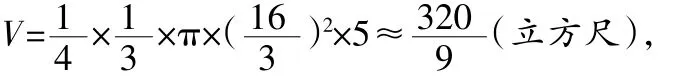
又1斛米的体积约为1.62立方尺,
多数学生对知识点熟悉,一看就会,一做就错。学生特别是文科生在计算方面存在缺陷。具体分析文科学生在计算方面出错的原因大致为:
①概念不清,性质不熟。
②先天计算能力差,没有遇到清楚详细的示范。
③公式理解不够,记错公式。
④审题不清,练习机会少。
⑤方法不对,没有考虑到长远解决此系列问题的方法。
⑥估算能力的培养不够。
教师在教学中应如何提高文科学生的计算能力?
1.注重学生错题过程的研究,收集学生错题,建立错题档案库,针对性讲解,对症下药,指出问题所在,提炼复习基础知识。注意学生的计算小错误,不可轻视,往往是计算性质用错,形成习惯,顽疾不清,永成恶患。如比较常见的学生错误是:除法分配律葬÷(遭+糟)=葬÷遭+葬÷糟,符号的计算-(-1)3=-1,函数去分母错误地去分母等。这样的错误,教师一旦发现,就要立刻纠正,否则就会变成学生的习惯性错误。
2.讲解例题或推导公式中,遇到计算复杂的过程,不要一带而过,先练后讲,有必要演示整个计算求解过程。比如:由椭圆定义推导椭圆标准方程,不要让学生自己看书本了事,一定要带着学生一步一步算一遍,让学生体会推导的过程。
3.学习新公式,设置情境,让学生在理解的基础上推导公式,并找出公式特点,帮助记忆。如:教学等差数列的定义及性质时,可以采用形象教学法,让学生切身体会到等差数列的规律,才能理解掌握好定义和性质。初次出现的计算,带着学生做一遍,示范一次,找到又快又准的方法演练一次。
4.注重通法和巧法,掌握计算技巧,如:有理式混合运算过程中不化简,因为可乘除约分,最后结果才化简。解二元一次方程组时用代入法消元后,可用跟踪系数法,又快又准地得到一元二次方程。
5.给学生纠错的空间、时间。同桌间、同学间互相找错误。除了思维的整理、学习,剩下就是计算的过程。讲得多,听得多,不如练得多。熟能生巧,由量变到质变。多练基础重要的计算,重要公式多练多记。如:解一元二次方程,多处要用,有空就练;配方法,求圆的标准方程,不用死记公式;点到直线的距离公式等。
6.初高中结合,从长远计算角度出发,采用适当方法。如:不用配方法解方程,而用公式法和因式分解法,目的是以后学会解一元二次不等式。不用最值公式求二次函数的最值,而用配方法或代入对称轴求最值,因为文科学生记公式难,容易错。
7.针对选择题,提高文科学生的估算能力,教会他们用特殊值法、排除法解题,可以在最短时间内得到正确的结果。例如:2017年高考全国卷1卷第8题:函数的部分图象大致为( )
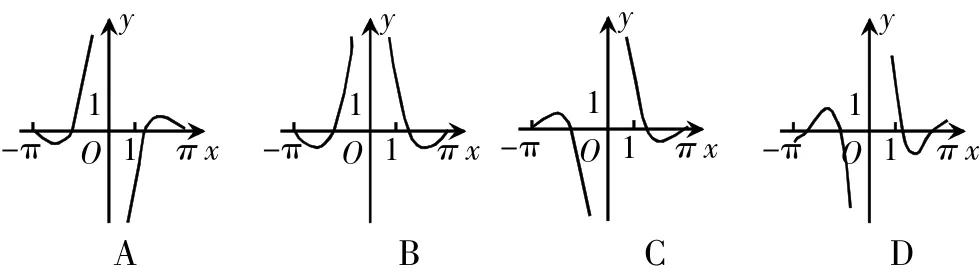
此类题教会学生用特殊值法估算:取曾=1,-1,π估算赠值的正负即可。再例如:(2017·全国Ⅰ卷,文 12)设粤,月是椭圆长轴的两个端点,若悦上存在点M满足∠粤M月=120°,则m的取值范围是 (A)
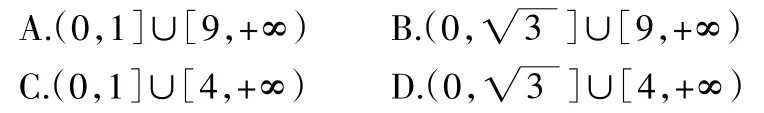
8.鼓励学生,常练基础题,提高学生自信心。每天让学生练习适量基础题,让他们在练习中体会成功的喜悦,提高自信心。
虽然这两年全国高考文科数学平均分很低,但只要教师引导学生抓住基础公式的理解和运用、注重基本解题思想的使用,再让学生多注意计算技巧和解题方法,文科数学并不会那么难学。

