鸭嘴开合控制机构张角误差分析
焦灏博,刘姣娣,曹卫彬
(石河子大学 机械电气工程学院,新疆 石河子 832000)
0 引言
移栽机作业一般是由鸭嘴开合控制机构扎穴植苗来完成穴盘苗的移栽,栽植鸭嘴在闭合接苗、扎穴入土、张开植苗过程中[1-7]反复张合,磨损严重,造成栽植鸭嘴机构开合幅度变小,钵苗无法落入植苗穴孔中,致使移栽植苗失败问题,加大了钵苗移栽的漏苗率[8]。因此,以鸭嘴开合控制机构的工作过程为基础,以机构关节布局和关节运动位移为切入点,研究移栽机鸭嘴开合控制机构移栽钵苗精度是很有必要的。许多学者对鸭嘴开合控制机构做了大量的研究,如栽植鸭嘴曲面优化,栽植鸭嘴控制机构的杆件参数优化设计等。陈建能等[9]针对钵苗在栽植嘴内运动时间过长而无法及时落入苗沟或穴坑造成的栽植失败问题,将钵苗相对栽植嘴的运动分为与栽植嘴壁面碰撞、平面运动和沿栽植嘴壁面下滑3个阶段,分别建立了各阶段钵苗的运动微分方程。金鑫等[10]对膜上移栽钵苗栽植机构进行了运动分析和参数优化,得到了一组符合膜上移栽钵苗直立度较高和不撕膜的农艺要求的最优参数值。刘姣娣等[11]为了减少移栽机在移栽钵苗过程对钵苗基质的损伤,对其执行机构进行了参数设计优化和试验分析。胡建平等[12]提出了一种行星轮多转臂式栽植器,阐述了其结构及工作原理,建立了栽植器末端运动轨迹方程,并引入特征系数λ,得出不同λ时的栽植器末端动轨迹。赵匀等[13]基于双曲柄五杆水稻钵苗移栽机的结构形能下降,针对重要传动部件进行改进,开发了基于B样条拟合曲线的轻简化水稻钵苗移栽机构——拟合齿轮五杆水稻钵苗移栽机构。由于栽植鸭嘴反复张合,造成磨损严重,使得鸭嘴开合控制机构开合幅度变小[14-15],钵苗在栽植嘴无法落入苗穴,导致移栽时漏苗现象出现。因此,利用参数优化的方法虽然改善机构的工作性能,但由于机构长时间运动,使得工作部件磨损,尤其是高副关节部件的磨损使得机构参数改变,造成机构工作性能变差。本文通过研究鸭嘴开合控制机构中高副关节位移变化,将其高副产生的微小位移融入相邻低副关节尺寸中,以消除高副关节产生的微小位移与高副关节磨损产生的微小间隙相互抵消的缺陷,使鸭嘴开合控制机构的设计精度得以保持,工作寿命得以延长。
1 鸭嘴开合控制机构原理
鸭嘴开合控制机构如图1所示。该结构与栽植机构串联,原理如图2所示。其中,构件①与构件④构件构成移动副,同时构件①与构建②构成线面接触的高副;构件②与构件④构成转动副,同时构件②与构件③构成线面高副;构件③与构件④构成转动副。鸭嘴开合控制机构的运动过程:构件①水平移动时推动构件②绕构件④转动,同时构件②使得构件③绕构件④转动,鸭嘴片1、2分别固定在构件②和构件③上,构件②和构件③的夹角变化量为鸭嘴片1、2的张角大小。同时,定义BH的长度为l1,BC杆长为l2,其变化量为△l2;CD杆长为l3,DE杆长为l4,其变化量为△l4;CE杆长为l5, ∠ABC为β1,其变化量为△β1;DE杆与竖直方向的夹角为β2,其变化量为△β2;∠CDE为β3,其变化量为△β3;CD杆与竖直方向的夹角为β4,其变化量为△β4;∠BCD为θ。通过对机构的原理和运动过程分析进一步的探究发现:现有的鸭嘴开合控制机构中,高副关节之间的构件产生相对运动的位移量很小(微小位移),微小位移过小,长时间作业将会与高副关节磨损的间隙相互抵消,导致鸭嘴开合的角度变小,移栽钵苗无法落入植苗穴孔, 造成钵苗移栽失败。本文将高副关节位移转移到低副关节尺寸中,使高副关节与低副关节位确保鸭嘴栽植开合角度大小的稳定性,解决鸭嘴开合控制机构堵苗问题[4]。

图1 鸭嘴开合控制机构Fig.1 Opening and closing mechanism of the planting-duck
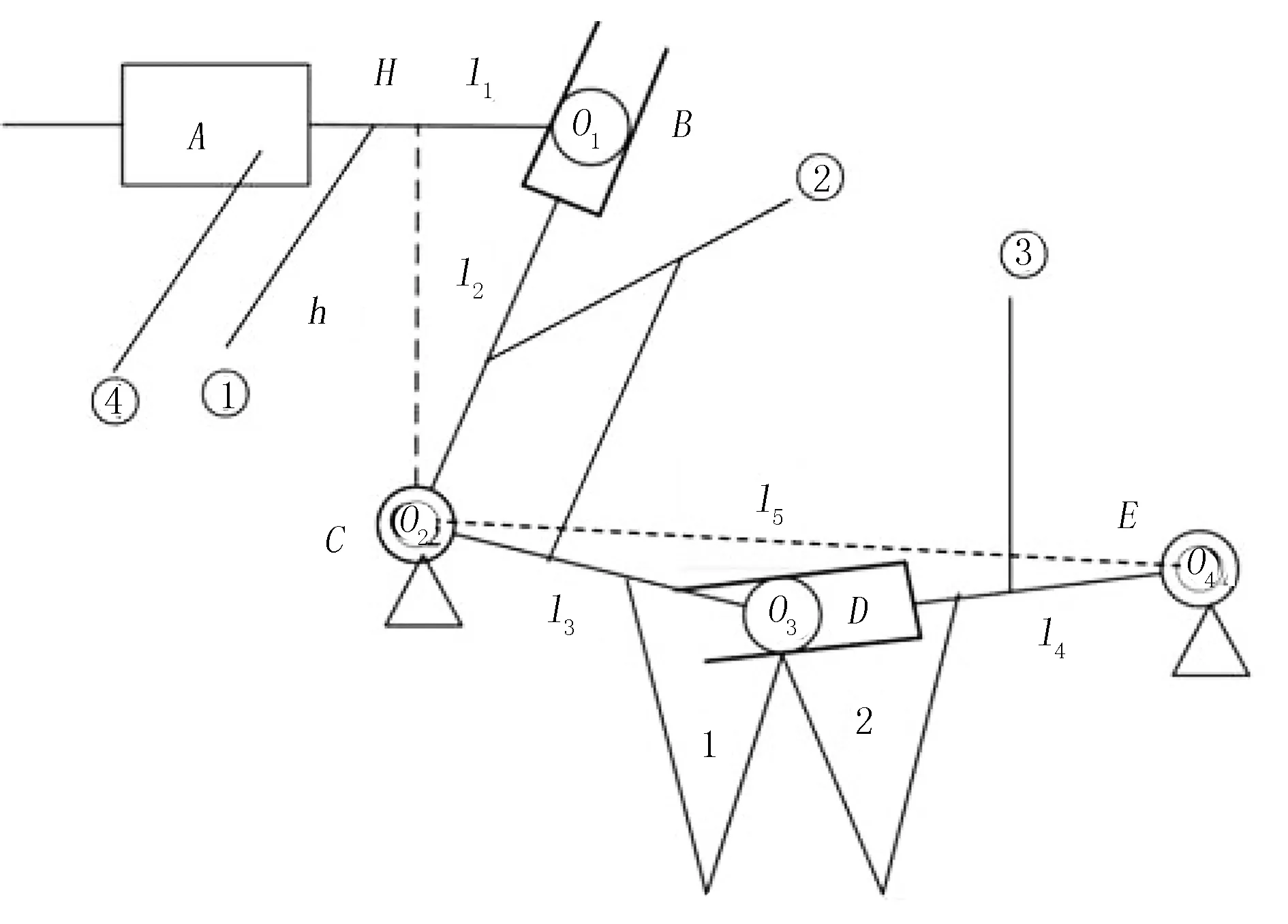
图2 鸭嘴开合控制机构原理
2 高副关节位移数学模型
鸭嘴开合控制机构的高副关节产生微小位移的大小直接影响鸭嘴栽植的开合角度大小。采用高副关节微小位移融入低副关节尺寸,其微小位移越小,机构的稳定性越好[15],因此需要对微小位移进行量化分析和参数优化。建立鸭嘴开合控制机构的高副关节构件的位移参数数学模型,以其构件运动位移最小为优化目标函数,在约束区域内寻求目标函数的最优解,求取最优解对应的设计变量值。由于设计要求鸭嘴栽植张角变化范围为0°~60°[11],图1中构件①与构件②之间l2、构件②与构件③之间l4的末端高副关节位移都存在微小变化,需要对产生位移进行数学建模与影响位移变化的参数进行分析优化。
2.1 鸭嘴张开与闭合位置l4位移变化数学模型
当鸭嘴处于闭合状态时,l3,l4,l5构成三角形,由正弦定理可得
(1)
整理(1)式得
(2)
鸭嘴在张开与闭合过程中,鸭嘴张角变化量为△β3,当鸭嘴处于张开时,由正弦定理可得
(3)
由式(2)、式(3)得杆件l4的长度变化量△l4为
图1中,存在垂直方向平行关系,则
β3=β2+β4
(5)
△β3=△β2+△β4
(6)
由于构件②和构件③成对称分布,按左右对称关系得
β2=β4
(7)
△β2=△β4
(8)
由式(5)~式(8)得
β3= 2β2
(9)
△β3=2△β2
(10)
通过机构的空间布局的几何分析得
β2∈(0,90°),β3∈(0,180°)
由鸭嘴开合控制机构的工作空间分析得l5的取值范围为0≤l5≤100 mm。通过以上分析得出,l4的位移变化△l4的数学模型为
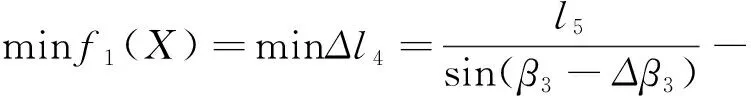
优化参数的约束条件如下:g1=-β3≤0,g2=β3-180≤0,g3=l5-100≤0,g4=-l5≤0。
△l4的数学模型的设计变量为X=[β3l5]T。基于软件MatLab建立△l4数学模型如图3所示。杆件l5长度对△l4的数值影响显著,而β3角位移变化对△l4的影响不明显,通过坐标值分析确定l5与β3的最优值。根据优化目标△l4的数学模型得出:当β3角位移一定时,△l4目标函数与设计变量l5呈线性关系,因此杆件l5长度小有利于减小l4的变化量△l4。由图3坐标值分析得出,当β3=163.48°时,l4的位移变化△l4取得最优值,将角位移β3代入l4的位移变化量△l4数学模型,得出△l4=-0.0023l5。根据鸭嘴开合控制机构的运动空间,初步取l5=50mm,此时l4的位移变化量△l4=-0.1132 mm。其中,△l4为负值时表明该高副关节的作用点O3沿着l4减小的方向运动。
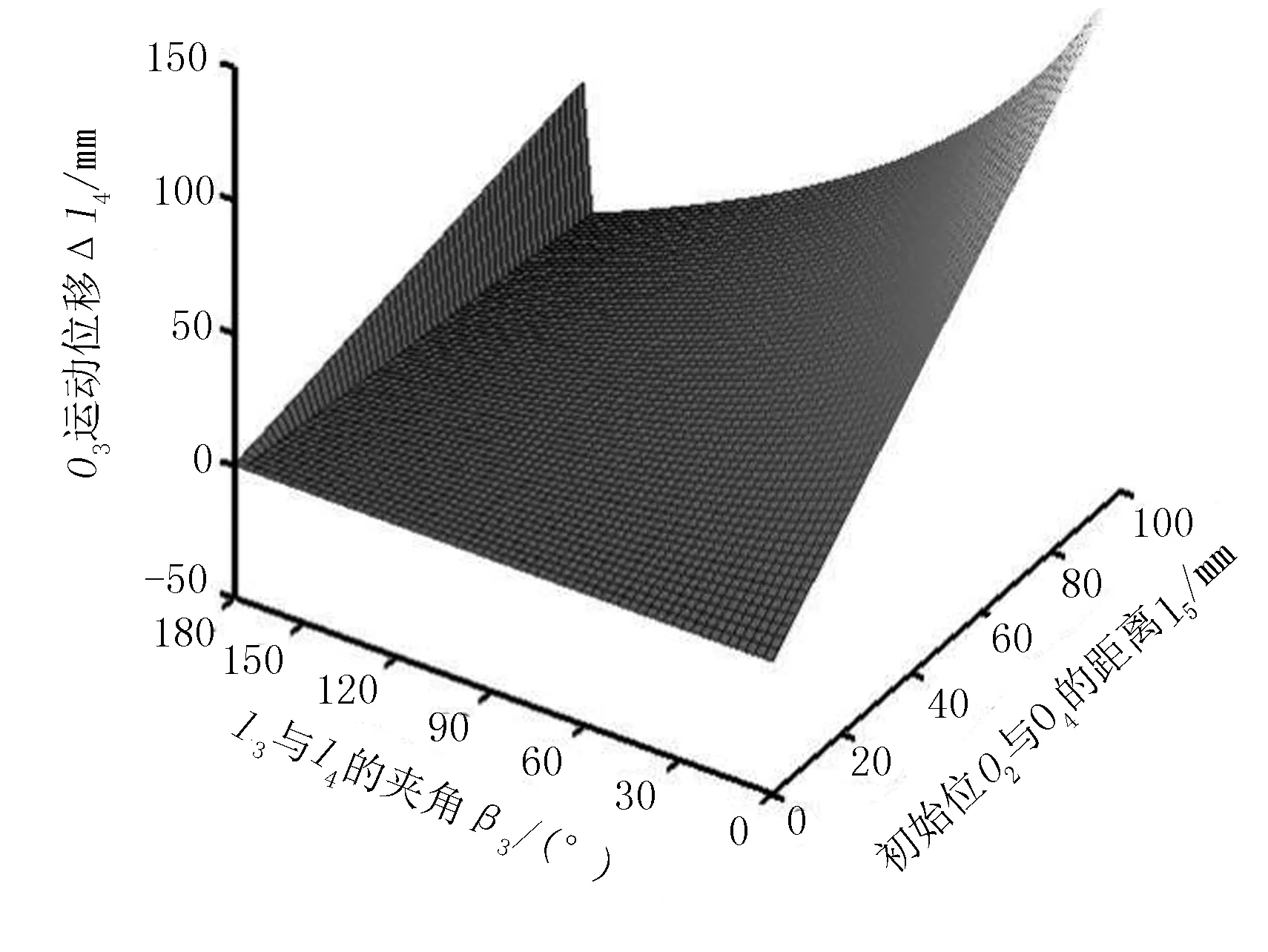
图3 △l4的数学模型
2.2 鸭嘴张开与闭合位置l2位移变化数学模型
当鸭嘴处于闭合状态时,h、l2、l1构成三角形,由正弦定理可得
(11)
鸭嘴在张开与闭合过程中,鸭嘴张角变化量为△β1,当鸭嘴处于张开时,由正弦定理推出

l2的长度变化量△l2为
△l2=l2-1-l2
(13)
由式(11)~式(13)得
图1中,鸭嘴开合控制机构存在几何关系为
β1=θ+β2-90°=98.52°
β1-△β1=θ+β2-△β2-90°=83.52°
由图1的工作空间分析可得θ∈(0,180°),且O1与O2的垂直距离h不宜过长,h范围为0≤h≤100mm。
由以上分析得出l2的位移变化△l2的数学模型为
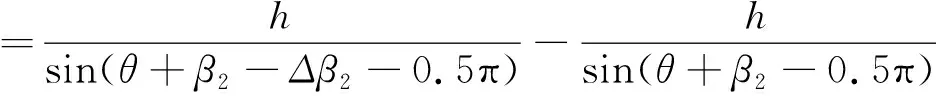
确定优化参数的约束条件如下:g1=-θ≤0,g1=-θ≤π,g1=-h≤0,g1=h-100≤0。
l2的位移变化△l2的数学模型的设计变量为X=[θh]T,基于MatLab建立△l2数学模型如图4所示。O1与O2的垂直距离h长度对△l2的数值影响显著,而θ角位移变化对△l2的影响不明显,可通过坐标值分析确定h与θ的最优值。由优化目标△l2的数学模型得出:当θ角位移一定时,△l2目标函数与设计变量h呈线性关系,因此O1与O2的垂直距离h长度小有利于减小l2的变化量△l2。由图3分析得出:当θ=106.78°时,l2位移变化△l2取得最优值。将角位移θ代入l2的位移变化量△l2数学模型,得出△l2=-0.004 7h。根据鸭嘴开合控制机构的运动空间,初步取h=30 mm,此时l2的位移变化量△l2=-0.1419 mm。其中,△l2的负号表明该高副关节的作用点O1沿着l2减小的方向运动。

图4 △l2的数学模型
综上所述,鸭嘴开合控制机构的两个高副关节均存在微小位移。因此,鸭嘴开合控制机构长时间工作,两处高副关节的磨损间隙将会与产生的微小间隙相互抵消,导致鸭嘴张角变小,钵苗无法顺利落到苗穴。为此,将微小位移融入低副关节,消除鸭嘴开合控制机构的高副位移产生微小位移对移栽钵苗成功率的影响。
3 微小位移融入与误差分析
将鸭嘴开合控制机构高副微小位移融低副关节尺时,其低副关节的选择是研究的关键点。融入的低副关节选择是否合适关系到鸭嘴开合机构运动的稳定性,具体体现在:①从工作性能角度考虑,影响鸭嘴开合的轨迹、移栽钵苗直立度与鸭嘴对地膜的干涉[17-19];②从动力学角度考虑,关节选择不当会出现关节磨损严重,需要提高材料性能来降低磨损[20-23];③从机械误差角度考虑,关节选择不当会明显加大栽植鸭嘴张角的误差,鸭嘴张角控制性能降低[24];④从振动学角度考虑,关节选择不当,关节间隙使机械振动强度增大,影响移栽机其他部件传动精度[25]。因此,选择鸭嘴开合控制机构高副微小位移融低副关节尺寸的原则是:将鸭嘴开合控制机构高副微小位移融低副关节尺寸,且保持融入关节原来的传动关系。
3.1 微小位移融入关节与融入量的确定
由于移动关节作水平运动时,添加垂直方向的移动不影响其水平运动;而转动关节在绕其轴转动时,添加沿着径向移动使关节转动位置改变。结合鸭嘴开合控制机构高副微小位移融低副关节尺寸的原则,选择移动关节作为鸭嘴开合控制机构高副微小位移的融入关节。图1表明:△l4产生变化的相邻关节O2与O4都为转动关节,不能将微小位移融入到转动副关节尺寸,因此选择l2的变化量△l2在垂直方向的分量位移进行融入,将其融入到构件①和④的移动关节的垂直方向尺寸中,其融入量记为△s。△s融入该移动关节的方法如图5所示。由投影定理得
△s=△l2sin(β1-△β1)
β1-△β1= =83.52
由此得出:△s=-0.1410 mm,取△s=-0.15 mm。图5中,由于鸭嘴开合控制机构构件l1产生融入量△s,杆件l1出现微小倾斜,产生位置误差2δ,由投影定理得
(15)
微小位移融入关节尺寸之后的机构原理如图6所示。其中,构件①与构件③构成的关节存在平动与微小的转动,应按高副计算,包括低副数PL=3 ,高副数PH=2, 活动构件数N=3,得出自由度F=1。因此,将鸭嘴开合控制机构高副微小位移融入低副关节尺寸,可以有效减少关节磨损,使鸭嘴开合控制精度稳定。
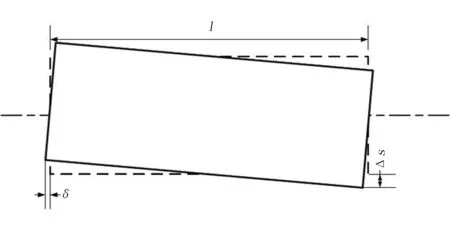
图5 △s融入移动关节方法

图6 改进后鸭嘴开合控制机构原理
3.2 微小位移融入关节后的误差分析
鸭嘴张角误差的大小影响鸭嘴控制机构的运动规律,采用机构位置误差传递矩阵法分析栽植机构末端鸭嘴张角误差[26],则
n11=C01C12[1 0]T
(16)
n21=C03[1 0]T
(17)
其中,n11为构件②对构件③作用线的方向向量,n21为构件②相对于构件③的运动线方向向量,C01、C12、C03为坐标变换矩阵。由图7得:鸭嘴完全张开为鸭嘴开合终了位置,θ0=0°。
(18)
(19)
(20)
由式(18)~式 (22)得:l3=27.21 mm,l2=30.20 mm,l6=46.12 mm,θ1=58.28°,θ2=arcsin(l3sin(β3)/l5)+△β2=23.52°。
构件①按图5的方法进行微小位移融入后,当l=100 mm时,杆件产生的位置误差2δ=[4.02×10-40]T。
σ=E1·(C01δ)
(22)

(23)
由式 (16)、式(17)、式(23)、式(24)得出传递到杆件l4的误差σ为
σ=[1.74×10-40]T
将杆件l4的误差σ转化为鸭嘴张角误差为R(△β3),即
通过鸭嘴张角的理论误差分析得出:在微小位融入关节尺寸后,鸭嘴张角误差很小,仅为0.035°,对鸭嘴机构的开合影响几乎不存在[9]。因此,将高副关节微小位移融入低副关节尺寸的方法,可以有效减小执行机构末端的位置误差。
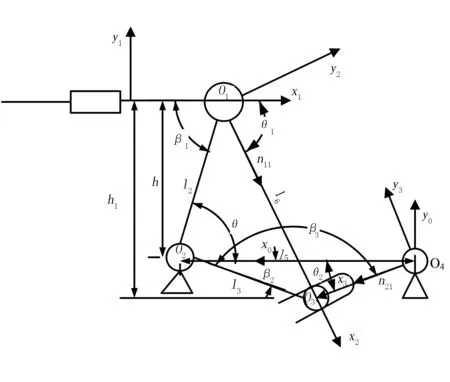
图7 鸭嘴开合控制机构的局部坐标系
4 结论
1) 鸭嘴开合控制机构的高副关节产生微小位移直接影响鸭嘴栽植的开合角度大小,用高副关节微小位移融入低副关节尺寸,消除机构磨损间隙,对微小位移进行量化分析和参数优化,建立鸭嘴开合控制机构的高副关节构件的位移参数数学模型。基于MatLab对△l4数学模型分析得出:杆件l5长度对△l4的数值影响显著,而β3角位移变化对△l4的影响不明显。
2)构建l2的位移变化△l2的数学模型,h长度对△l2的影响显著,而θ角位移变化对△l2的影响不明显。根据优化目标△l2的数学模型得出:当θ角位移一定时,△l2目标函数与设计变量h呈线性关系;当h=30mm,θ=106.78°时,l2位移变化取得最优值△l2=-0.1419mm。
3)利用MatLab优化与误差传递矩阵的理论进行融入误差分析计算得出:高副关节微小位移融入低副关节尺寸时,鸭嘴张角产生的误差为0.035°,对鸭嘴机构的开合影响几乎不存在。因此,将高副关节微小位移融入低副关节尺寸的方法,使机构末端执行构件的设计精度保持稳定和工作寿命得以提高,同时为存在高副机构的优化设计提供新的方法,为机构高低副关节的最优布局提供一种新的思路。

