场地膜秆分离装置的数值模拟研究
张姚斌,王春耀,刘梦霞,罗建清
(新疆大学 机械工程学院,乌鲁木齐 830047)
0 引言
地膜覆盖技术可以提高地温,加快根系生长,适合微生物的增殖,使无机盐的转化速度大大提高,使农作物产量提高,具有诸多优势,因此广泛被农业生产者使用[1-3]。然而,地膜技术的应用为农业生产带来巨大经济效益的同时也产生了很大的负作用,即残留的地膜破坏土壤结构,影响耕地质量与透气性,不同程度地抑制了农作物的生长发育,造成减产。残留地膜降低了土壤微生物的活性,阻碍了土壤矿化释放及肥力提高,所以对地膜的回收和分离迫在眉睫[4]。本文采用了数值模拟的研究方法,对不同工况下的膜秆分离装置进行模拟仿真,分析腔体内流场的压力及速度分布,从而为膜秆分离装置选择了合适的风选参数范围。
1 方法
1.1 风选过程的工作原理
膜秆分离装置的基本原理是根据不同密度的物料所具有的悬浮速度差来进行分离。质量较大、密度较大、悬浮速度较大的粗细棉秆在自身重力作用下依次下落,而密度小、质量轻、悬浮速度较小的地膜随着水平向前的气流输送到较远的物料出口,从而地膜与粗细棉秆进行了分离,其风选原理如图1所示。本文采用悬浮实验台测量膜杂的悬浮速度,得到粗棉秆的悬浮速度为8~10m/s,细棉秆的悬浮速度为6~8m/s,地膜的悬浮速度为2m/s。由此可见,地膜与棉秆的悬浮速度相差较大,因此利用其悬浮速度差分离出地膜[5-7]。其悬浮试验台如图2所示。
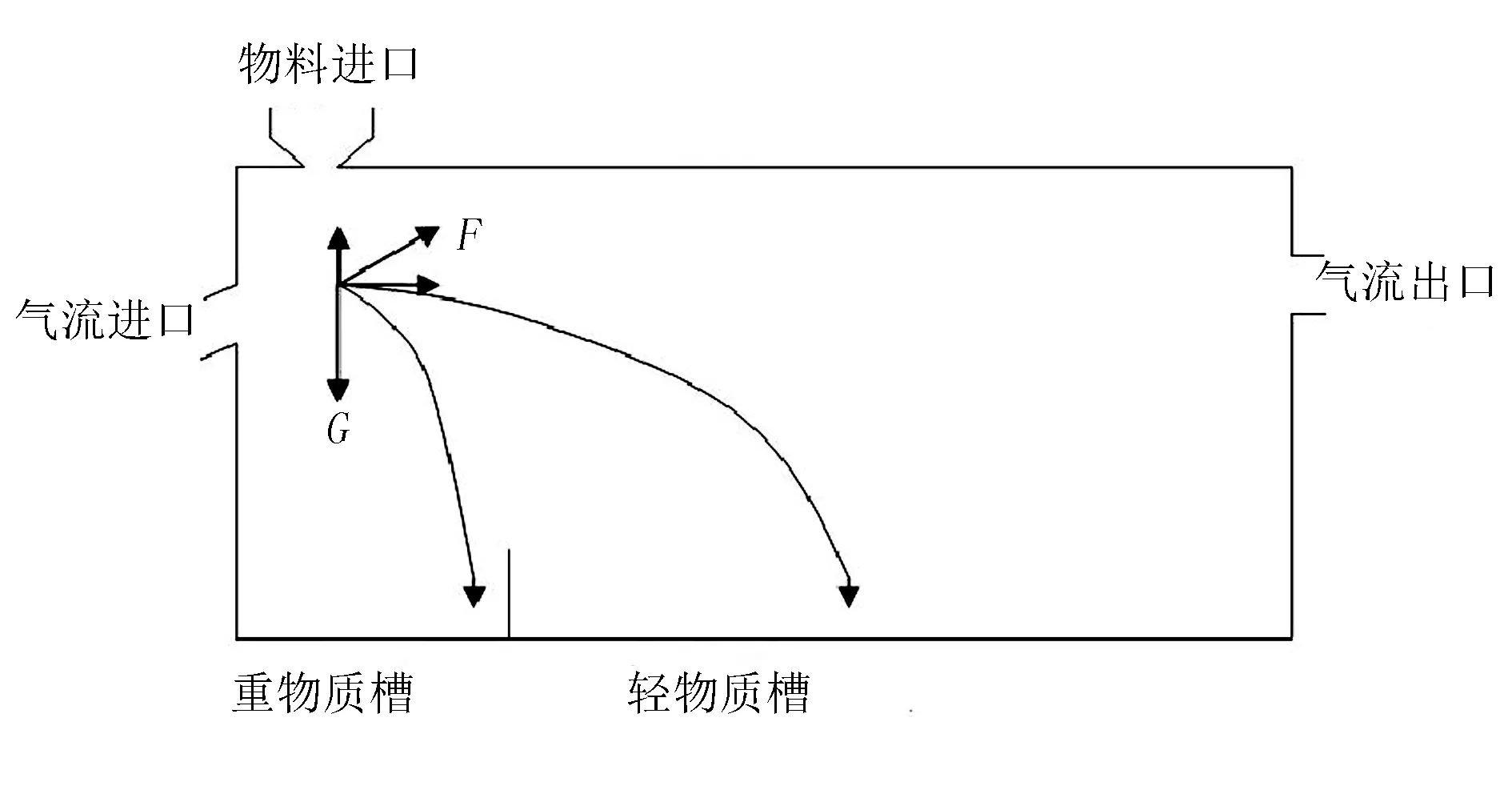
图1 膜秆分离装置气流分选原理示意图

图2 悬浮试验台
1.2 数学模型
本文通过改变送风速度、送风角度和进料口的位置来分析其流场内部的速度和压力分布,找到一种较佳的风选参数范围。
流体在腔体内的流动为湍流流动[8-9],膜秆分离装置内部流场遵守质量守恒定律及牛顿第二定律,定义腔体内部的流场是不可压缩流场,湍流流动采用k-ε模型,在直角坐标条件下的各个控制方程如下:
1)质量守恒方程为
(1)
对于不可压缩的流体,密度ρ设定为常数,那么式(1)可化简为
(2)
2)动量守恒方程(即N-S方程)为
(4)
(5)
3)k-ε湍流方程为
模型中的常数按照文献[10]选取C1ε=1.44,C2ε=1.92,σk=1.0,σε=1.3,建立完整的数学模型,进一步进行数值模拟分析。
1.3 网格划分和边界条件
1.3.1 网格划分
对膜秆分离装置风选流场进行数值模拟研究,求解的几何区域为膜秆分离装置的几何空间体。筒体的前侧面设置有进料口和送风口,筒体的后侧面和筒体上的孔洞设置为出风口,采用UG建模其简化图如图3所示。模型的尺寸参数设置如下:
滚筒直径/mm: 1 200
滚筒长度/mm:4 000
送风口尺寸/mm:600×150
进料口尺寸/mm:400×200
膜秆分离装置几何模型的网格划分类型采用适用性很好的Tgrid混合网格。Sizing的设置中,Relevance Center设置为Fine,Interval size Seed 设置为 Active Assembly,Smoothing 设置为Medium ,Transition 设置为Slow ,Span Angle Center设置为Fine ,共划分了 15 890个节点、79 622 个单元、164 291个面。划分后的网格如图4所示。

图3 膜杆分离装置简化图

图4 场地膜秆分离装置的网格划分
1.3.2 边界条件
根据地膜分离装置腔体的特点,设置送风口为Velocity-inlet,送风速度为10m/s,出风口为Outflow,Flow Rate Weighting为 1;物料是连续送入模型,忽略气流的散失,因此进料口设置为Wall;其余壁面的边界条件设置为Wall。
2 数值模拟与结果分析
2.1 初始模型的模拟分析
运用ANSYS的Fluent模块对膜秆分离装置进行流场分析,得到整个内部的压力和速度分布。图5的横坐标代表腔体的长度,单位为mm;纵坐标代表流场压力,单位为Pa。图6的横坐标代表腔体的长度,单位为mm;纵坐标代表流场速度,单位为m/s。
分析图5和图6可以看出:模型内部的压力先减小然后逐渐增大,在送风口下端及模型前端顶部存在低压区,且压力值变化较大;在模型长度X<0.25m范围内,压力值减小,最小压力为2.12Pa;在模型长度X>0.25m范围内,压力值逐渐增大,最大值为15.30Pa。流场压力在模型后端逐渐稳定,利于膜杂分离。即模型内部的压力呈现先减小后增大的趋势,且压力值在模型后端变化不大;腔体内的流体速度逐渐减小,且流体的速度在腔体的前半部分分布不均匀,各点的速度比较分散,不够密集,在后半部分速度分布较为均匀。在X>350mm范围内,速度基本保持在2m/s以下。
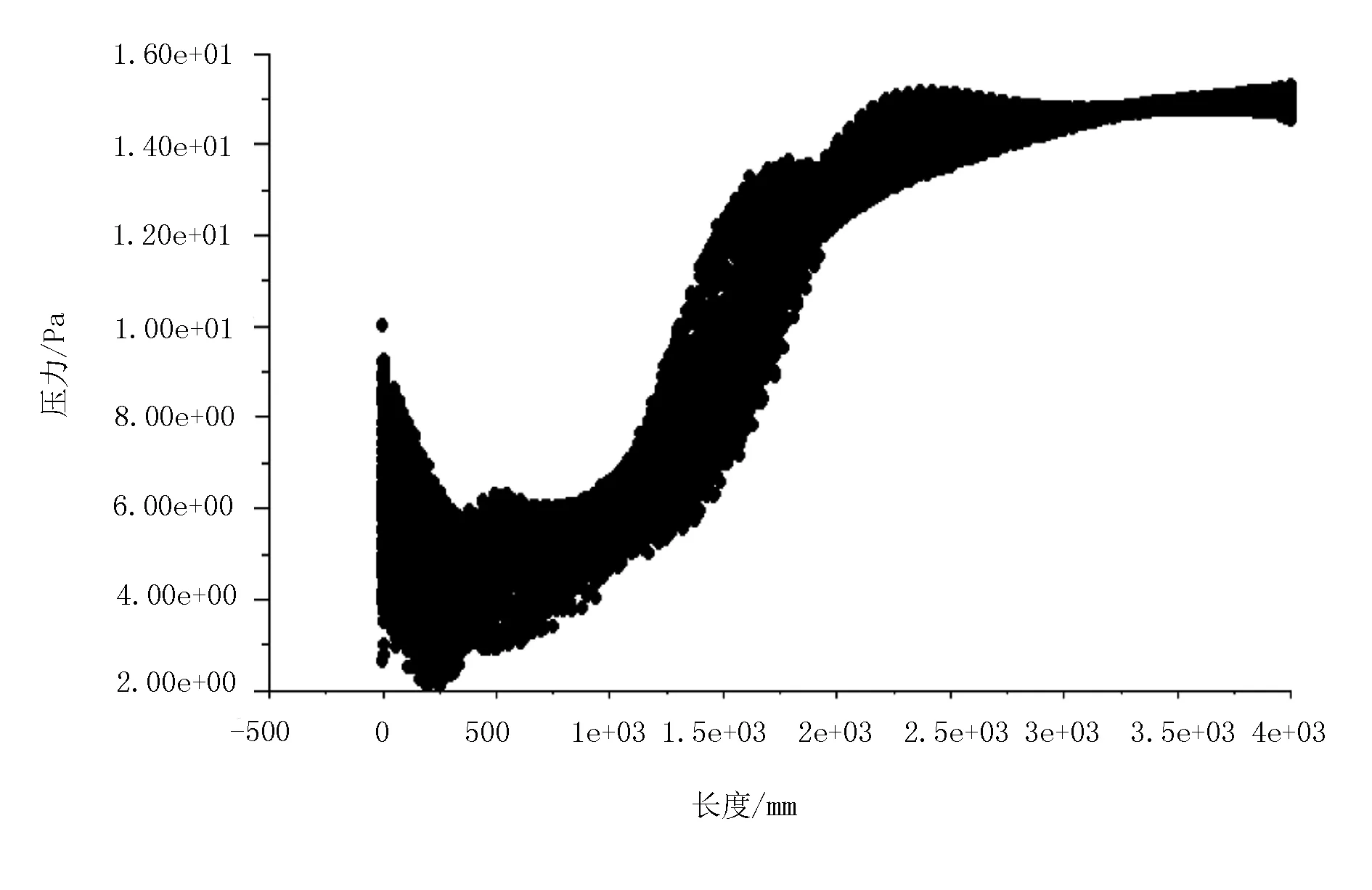
图5 流场的压力分布
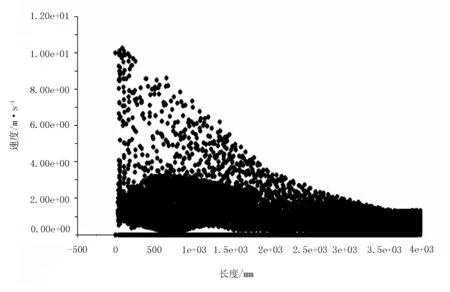
图6 流场的速度分布
2.2 送风速度的模拟分析
初始设备的送风速度为10m/s,不足以合理地分离粗细棉秆和地膜,因此增加送风速度为12、14、16、18、20m/s,分析送风速度的改变对膜秆分离装置内部流场和风选效率的影响。在膜秆分离装置的腔体水平方向上每隔100mm选出一个截面,共计选出40个截面,计算得到每个截面的压力及速度平均值,并绘制曲线。分析送风速度的改变对腔体内部流场的压力和速度分布的影响。图7为当送风速度改变时流场内部压力沿着腔体的改变,图8为当送风速度改变时流体速度沿着腔体的改变。
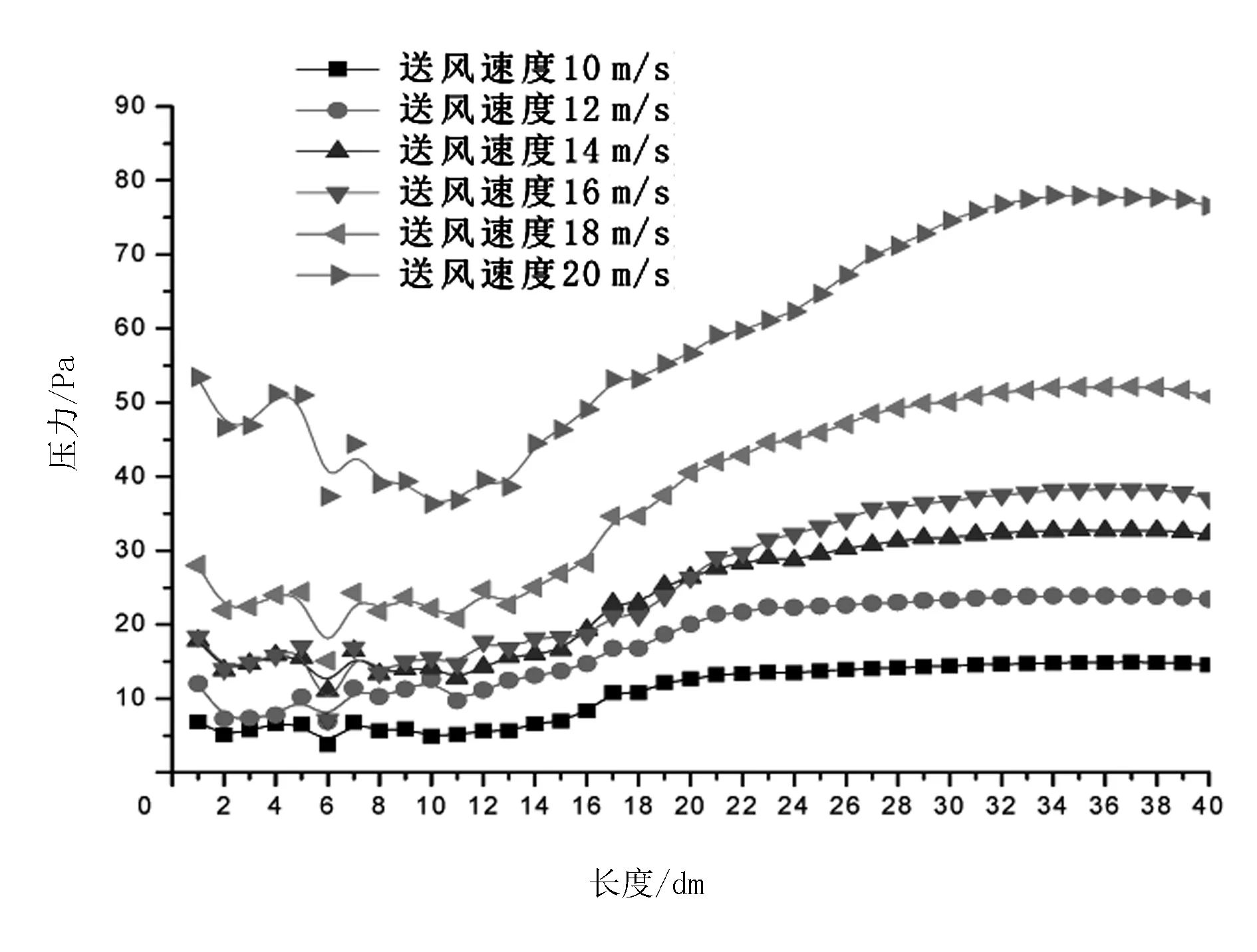
图7 送风速度改变压力的模拟分析
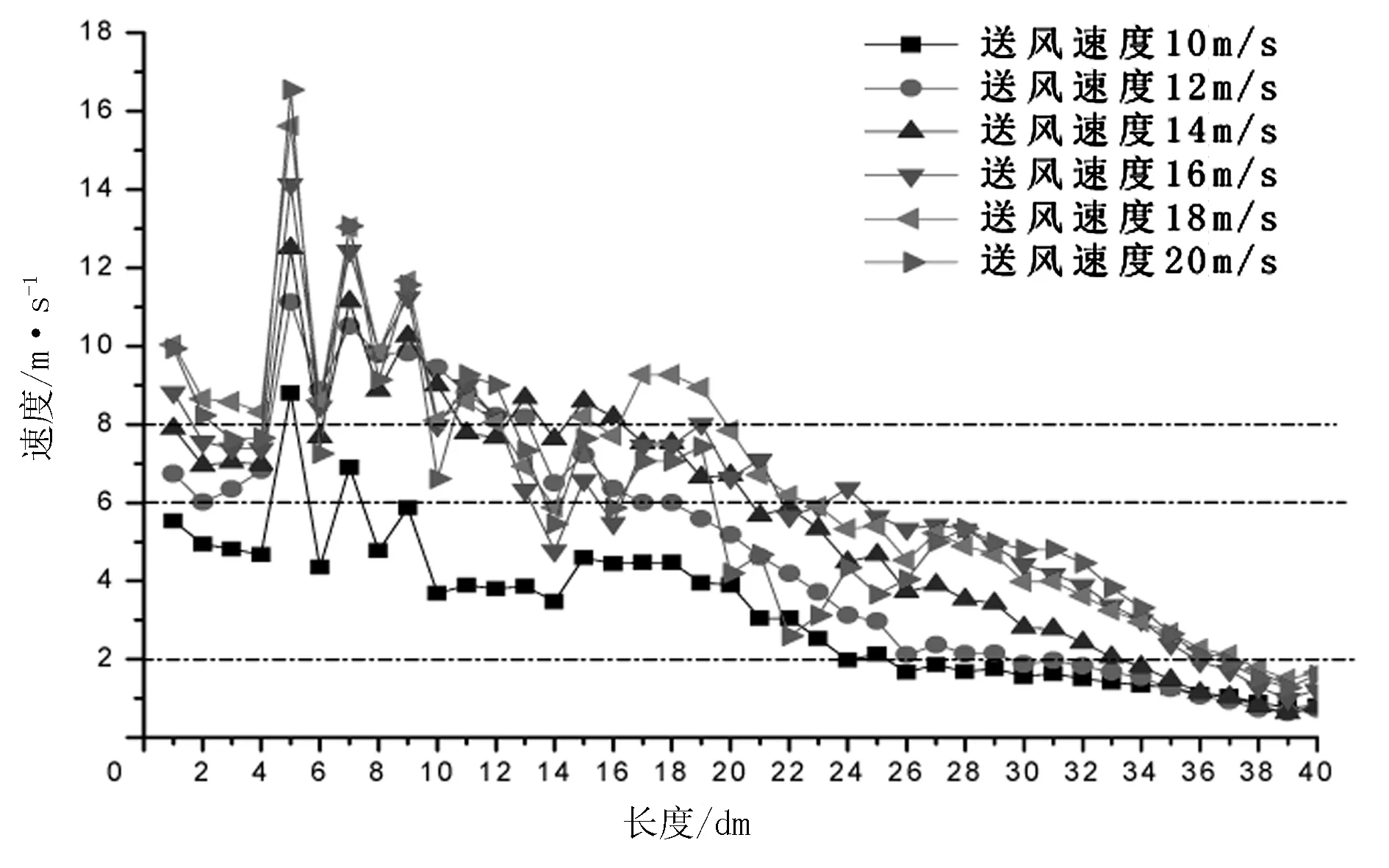
图8 送风速度改变速度的模拟分析
分析图7可知:随着送风速度的增加,模型内部流场压力均值变大;送风速度大于14m/s时,流场压力均值明显增加;送风速度大于18m/s,流场压力均值过大,且随着模型水平方向一直增加,其压力不稳定,不利于地膜的分离。
综上所述,当送风速度为14~16m/s时,模型内部流场压力稳定增加,且流场压力变化平缓,是较为适宜的风选速度。
分析图8可知:初始设备中,模型内部流场速度过小,模型内部基本无大于8m/s的区域;流场速度6m/s 综上所述,送风速度为16m/s较为合理。 初始设备模型的送风方向为水平送风(即无偏角度送风),通过改变送风上偏角度,将送风角度分别设置为送风角度上偏5°、10°、15°、20°,分析送风角度的改变对流场的影响。取截面方法与前面相同,计算得到的每个截面的压力及速度平均值,并绘制曲线,分析送风角度改变时对流场的压力和速度分布的影响。图9为当送风角度改变时流场压力沿着腔体长度的改变,图10为当送风角度改变时流体速度沿着腔体长度的改变。 图9 送风角度改变压力的模拟分析 图10 送风角度改变速度的模拟分析 分析图9可知:初始模型内各个截面的压力均值为正压;当送风角度上偏时,模腔体内部出现负压区,且随着送风角度的增加,负压值增大,负压区范围增大;送风角度为上偏5°时,负压区范围占整个模型的80%;当送风角度大于5°,模型内的流场压力均值为负值;送风口上偏15°时,流场负压值较其他工况条件为最大,最大负压为-25Pa;送风角度为20°时,模型内部的压力均值减小。 分析图10可知:随着送风上偏角度的变大,腔体内部的流体速度最大值变大;当送风角度上偏5°时,流场速度6m/s 综上所述,当送风角度为5°时,流场压力分布及速度分布较优。 设置模型的初始进料口位置为距离模型中心为400mm的位置,通过改变进料口的位置,即进料口上移30mm、进料口上移50mm、进料口下移40mm、进料口下移60mm,分析膜秆分离装置内部流场和风选效率的影响。取点方式不变,计算得到每个截面的压力及速度平均值,并绘制曲线,分析进料口位置的不同对流场的压力和速度分布的影响。图11为当进料口位置改变时流场压力沿着腔体的改变,图12为当进料口位置改变时流体速度沿着腔体的改变。 图11 进料口位置改变压力的模拟分析 图12 进料口位置改变速度的模拟分析 分析图11可知:进料口位置上移30mm时,流场内压力从负压区过渡到正压区,负压区范围较其他进料口位置为最大,约占整个模型的42.5%;进料口位置继续上移50mm时,流场压力从负压区过渡到正压区,负压区范围占整个模型的40%,负压值减小,进入正压区后,压力变大;随着进料口位置的上移,负压区范围减小且负压值变小;进料口位置下移40mm时和进料口位置继续下移60mm时,其腔体内部的正压区压力值小于初始模型的压力值。 分析图12可知:进料口位置上移30mm时,流体速度波动性很大,且流场速度V>6m/s的范围很小; 进料口位置上移50mm时,流场速度波动性大,流场不稳定,其流场速度V>6m/s的范围变化不大,流场速度2m/s 综上所述,当进料口位置下移60mm(进料口中心位置距离模型中心位置为340mm)时,为相对合理的进料口位置。 1)分析不同送风速度对膜秆分离装置内部流场和风选效率的影响,结果证明:送风速度为16m/s时为适宜风选膜杂的条件。 2)分析不同送风角度对膜秆分离装置内部流场和风选效率的影响,结果表明:送风角度上偏5°时,其风选效率较好。 3)分析不同进料口位置对膜秆分离装置内部流场和风选效率的影响,结果表明:当进料口中心位置距离模型中心位置为340mm时为合理的进料口位置。2.3 送风角度改变的模拟分析


2.4 进料口位置改变的模拟分析
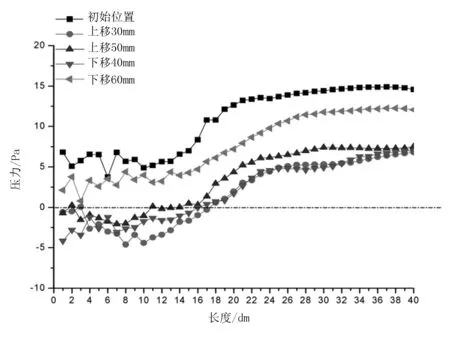
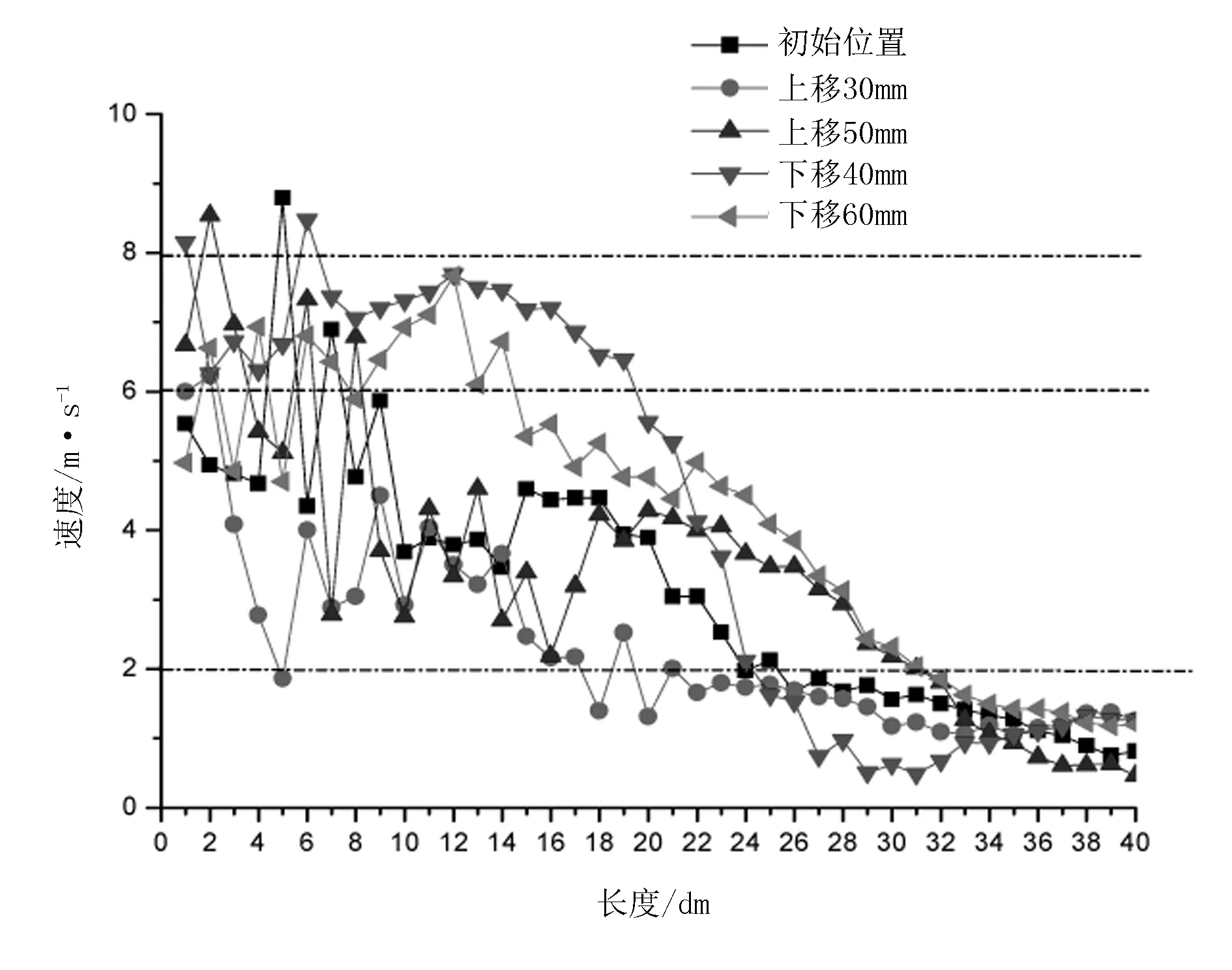
3 结论

