城市轨道交通网络的优化模型
王国宇 张嘉琪 张永利 丁明明 吕文英 纪楠
摘 要:本文以城市轨道交通网络建设问题为研究对象,将交通线路合理性和可达性作为限制条件,建立交通网络的多目标优化模型。此模型以总出行时间最少、线路总长度最小以及总换乘次数最少为目标建立多目标函数,并对模型进行求解。该模型可对可能的轨道交通线路进行筛选,得到最优的线路网络布局。
关键词:城市轨道交通 优化模型 多目标函数
中图分类号:U239.5 文献标识码:A 文章编号:1672-3791(2018)03(b)-0023-02
随着科技的进步,城市轨道交通在公共交通中的重要性越来越高。20世纪至今,国内城市纷纷开展轨道交通的研究,取得了不错的研究成果。本文通过分析轨道交通的特点,构建模型优化轨道交通的线路布局。
1 模型建立
1.1 模型目标及限制条件
1.1.1 模型目标。
目标Ⅰ:总轨道交通出行时间最少,即
式(1)中,为地区和之间的客流;为在其路径上所需时间。
目标Ⅱ:总的轨道交通线路长度最小,即
式(2)中:为交通线路;为二进制变量;1代表选择线路,0则不选。
目标Ⅲ:总换乘次数最少,即
式中:为总的换乘次数。
本文采取线性加权方法求解多目标规划模型,此目标函数则为:
其中:为线路总长度的权重;为总换乘次数的权重。
1.1.2 限制条件
将轨道交通的线路合理性和可达性考作为限制条件。
(1)轨道交通线路合理性。
其中:和分别为线路总长度最小值和最大值。
(2)任意两主要交通区域之间可达性:
1.2 路径
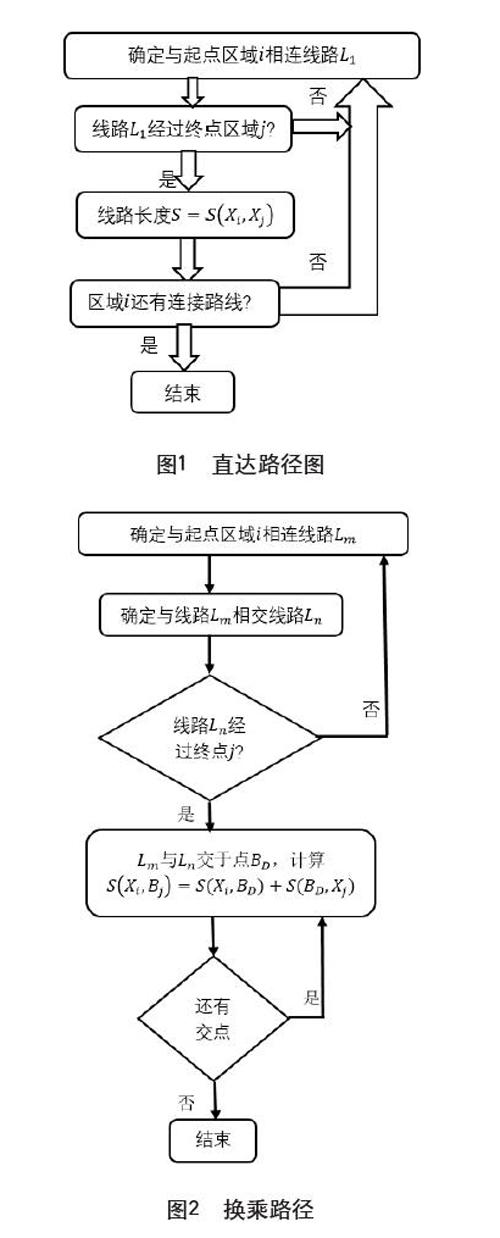
(1)直达路径如图1所示。
(2)换乘路径如图2所示。
2 模型求解
对此模型选取遗传算法求解。
2.1 编码与解码
采用0-1编码,假设备选轨道线路有条,代码依次为,染色体长度为。用“1”表示选择该线路,”0“表示不选该线路。
2.2 适应度函数
令为适应度函数。为第个个体的适应度,为目标函数最大值,为第个个体目标函数值。
2.3 限制条件处理
从群体中挑选两个个体,按以下规则进行比较。
(1)两个体均为可行解,适应度更大的更大概率进入下一代。
(2)两个体为一可行解和不可行解,可行解更大概率进入下一代。
(3)两个体均为不可行解,更接近最大适应度值的更大概率进入下一代。
2.4 遗传算法流程
(1)初始化种群数目、染色体长度、迭代总代数、交叉概率和变异概率。
(2)随机产生初始种群,迭代次数设为1。
(3)得出各个个体對应的解,代入模型中得到对应的路径二进制码,解码后再计算每个个体的适应度。比较个体适应度值,若迭代次数,则输出适应度值最小个体,否则进入下一步。
(4)使用精英机制,直接选择前代最优个体。
(5)两个不同的染色体根据交叉概率按照某种方式交换其部分基因。
(6)基因根据变异概率,进行变异,迭代次数,得到新种群,并转到第三步。
3 结语
以总出行时间最少、出行线路总长度最小及总换乘次数最少为优化目标,将交通线路合理性和可达性做为限制条件,建立了城市轨道交通网络优化模型。该模型为多目标优化函数,为城市轨道交通网络的优化提供了理论建议。
参考文献
[1] 胡汪源.基于时空网络的城市轨道交通乘务排班优化模型与算法[D].北京交通大学,2017.
[2] 叶青.城市轨道交通网络脆弱性分析与客流协同控制研究[D].西南交通大学,2016.
[3] 张旻沁.基于拓扑结构的城市轨道交通网络连通可靠性分析与优化[D].东南大学,2016.
[4] 李丽.基于复杂网络理论的城市轨道交通网络可靠性研究[D].北京交通大学,2015.
[5] 吕晓东.城市轨道交通列车运行交路问题研究[D].西南交通大学,2012.

