不等式解题中的“36计”

安徽省无为县牛埠中学(238351) 朱小扣

广东省兴宁市第一中学(514500) 蓝云波

不等式一直是高考和竞赛的重点,其解题方法千变万化,解题规律也难掌握.犹如行军打仗,唯有依计谋可胜.正所谓“上兵伐谋”.同样在不等式的解题中同样需要谋略.现列举几种解不等式题的计谋,以期抛砖引玉.

1.远交近攻

例1 设A,B,C是△ABC的三个内角,求证:sinA+

证明若A=B=C=60°,则若A,B,C不全相等,不妨设A＞60°,B＜60°,f(A,B,C)=sinA+sinB+sinC,则

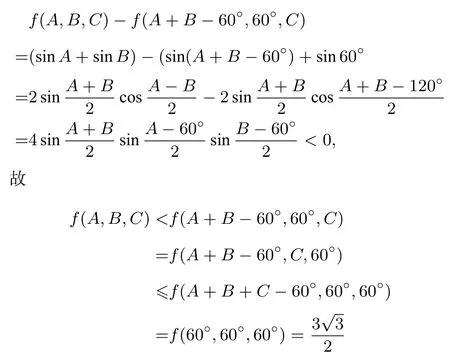
(显然A+B−60°,C中有一个大于或等于60°;有一个小于或等于60°).综上,可得

评析远交近攻是为了达到某个最优目标,从某个固定点出发,先近后远地分别调整各个部分,使每次更接近目标,进而顺利解题.

2.借刀杀人

例2a,b,c＞0,abc=1,求证:a4+b4+c4≥a3+b3+c3.

证明因为x＞0时,

再由常见不等式x−1≥lnx得:

a4+b4+c4−(a3+b3+c3)≥lna+lnb+lnc=ln(abc)=0,故a4+b4+c4≥a3+b3+c3.

点评利用x4−x3≥x−1及x−1≥lnx(x＞0)证明了不等式,实际就是利用借x−1这把“刀”去解题,达到“化曲为曲”.

3.借尸还魂

例3 (2015年山东省预赛第5题)已知x,y∈[0,+∞)且满足x3+y3+3xy=1,则x2y的最大值是___.

解将z看成−1,利用公式

而x2+y2+1−xy+y+x≥ 2xy+1−xy+y+x=xy+x+y+1＞0,故x+y=1,于是,

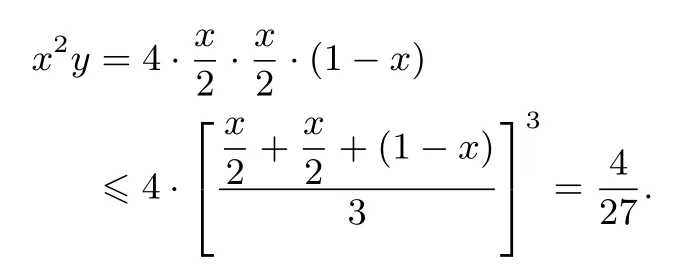
评析此类题着重考察化归能力,题目对部分同学来说很难.如果不会灵活运用公式,就不能解决好此类题.所以,解决此类题,必须要懂得“借尸还魂”,

4.李代桃僵

例4 已知x,y∈R且x2+xy+y2=1,求x2+3xy+2y2的范围.

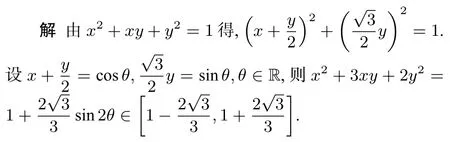
点评通过元与元之间的转化过渡,“李代桃僵”使问题能由繁变简,由难变易,通过换元能让学生更加体会数学中的千变万化的美.

5.釜底抽薪

例5 已知x,y,z＞0,求的最小值.

解令a=y+3z,b=4x+8z,c=3x+2y,则

于是

除了用分母换元法外,有时还可以用乘积换元法.

点评利用分母换元法,可以将复杂的分母简化,进而运用均值不等式使得问题能简单的解决.分母换元法在解决此类问题中均达到了“釜底抽薪”的效果.

6.无中生有

例6 设a,b,c∈R+,求证

简证不妨设a+b+c=1,则原不等式化为由切线法易得:需证即可.

点评因为左边式子是齐次的,故只需考虑a+b+c=1,因为假设a+b+c=s,则可设a=sa′,b=sb′,c=sc′,代入原不等式,即和a+b+c=1的情形一样.也就是利用换元法将非条件不等式问题转化成条件不等式,“无中生有”.

7.金蝉脱壳

例7 已知a,b∈R+,且3a+4b=1,求的最小值.

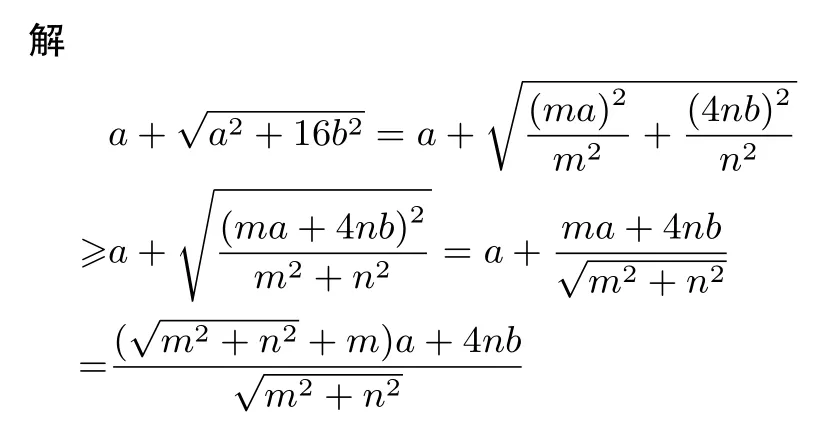
例8 (数学通讯问题309)已知a,b,c,d为正数,且a+b+c+d=1,试求的最大值.

点评通过权方和不等式(或其他不等式)将根号去掉,“金蝉脱壳”.使无理不等式有理化,进而求解.

8.上屋抽梯

例9 (文[1])已知x＞y＞0,xy=1,求的最小值.

解设则k就是所求的最小值,即3x3+125y3≥k(x−y),也即3x3+125y3+ky≥kx.由于xy=1,

例10 (2016年青年组)已知a＞0,b＞0,求的最小值.

令a+b=t,则

点评利用k值法可以将分式转化为整式,“上屋抽梯”,使得问题简化,从而能够顺利求解.

9.瞒天过海

例11 设a,b,c＞0,且21ab+2bc+8ca=12,求的最小值.

解令则问题转化为:在7xy+3yz+5xz=15的条件下,求的最小值.因为即x6y5z4≤ 1,所以

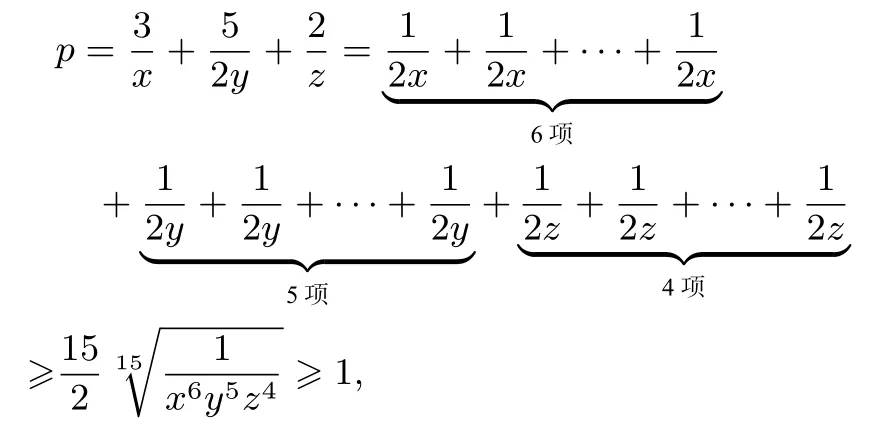
以上文[2]中的解法让人叹为观止,同时也让人摸不着头脑.受张艳宗老师的指导启发,笔者发现上解看似巧妙,实际上是先暗中运用了拉格朗日乘数法,确定了极值点,进而优化解法,使得解法简洁巧妙.

另解令

点评本种方法看似简洁玄妙,实则先利用拉格朗日乘数法求出最优解,然后用换元法使得解法简洁,“瞒天过海”.知道这些,就能了解很题配凑的技巧.类似题,像数学通报2080问题等.

总结古书有云:“兵者,诡道也”.用兵之道在于千变万化,在于出其不意.同样不等式的解题方法也是这样的.水无常形,兵无常势,唯有知其道,晓其法,笃其行,方能百战不殆,在不等式的解题中取得成功.限于水平,以上仅列举了八种不等式得解题计谋,期待各位不等式专家推广与总结.