一种基于数字音频信号的加密算法

张晓峰，贾晓强

（1.渭南职业技术学院机电工程学院，陕西渭南714000；2.渭南师范学院网络安全与信息化学院，陕西渭南714099）

在人们日常生活中，语音和图像是与听觉和视觉相关的信息，语音识别和图像处理和我们的生活息息相关。随着社会的进步、高科技的进步以及现代数字信号处理技术的飞速发展，语音和图像中的重要部分和复杂部分几乎都可以用数字信号处理手段来处理。语音信号的一系列处理步骤从理论到实际的产品开发经历了很长的一段时间，在这个过程中取得了巨大的进步。语音信号的一系列处理正间接与不同的行业与领域相融合，例如：工业流程中的语音监测、通讯系统的自动拨号、医疗卫生方面的生存援助系统等。在这些应用领域，为了提高语音信号的安全性，往往要对信息执行加密。

1 数字音频加密算法的概述

数字语音信号的加密，从字面意思简单理解为信息在传输过程中，容易被一些人轻易截取，加密，无疑就是发送者给一段原本清晰的语音信号（载体信号）加入一些复杂信号（嵌入信号），使原始信号不会轻易的被人获取。待接收者接受之后，对接收信号进行解密，恢复为原始信号，从而完成了语音信号的加密过程。

2 数字语音信号加密的设计方案

2.1 设计思路

根据具体语音情况对语音信号进行加密解密处理，并与原始信号进行对比分析。具体思路为：

1）对原始语音信号进行采样、嵌入语音信号的傅里叶变换；

2）进行语音加密，做变量不等量的叠加运算；

3）对叠加后的信号进行逆运算，原始语音信号的提取，恢复原始语音信号；分析恢复的语音信号和原始语音信号的的异同；

4）对原始语音信号进行抗噪声处理，并与原始信号作对比分析。

2.2 音频信号的嵌入与提取

1）音频信号的采集与嵌入

录制两段清晰的语音，时间不宜太长，分别定义为“chengdu.wav”和“tonghuazhen.wav”，将前者作为原始信号，后者为嵌入信号。

2）原始音频信号的时域及频域分析

将保存好的语音信号“chengdu.wav”文件利用相关函数在MATLAB软件中读出，如：

[x，fs，nbits]=wavread（'E:workchengdu.wav'）；

运行程序代码可得到原始语音信号的时域波形图，为了更方便直观的观察，并给出了原始语音信号时域图的三维立体图，如图1所示。

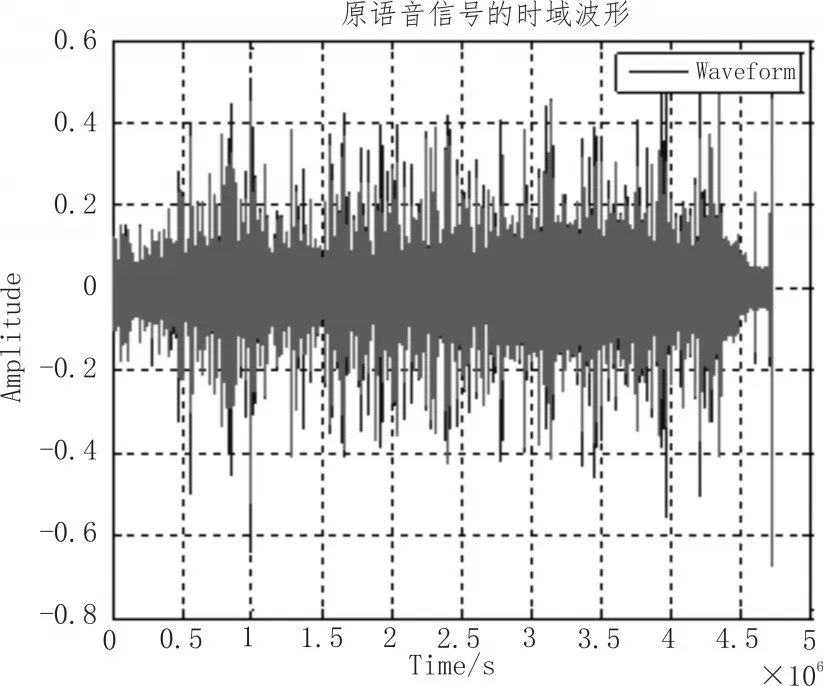
图1 原语音信号时域图

画出原始语音信号“chengdu.wav”的时域波形图，对原始语音信号进行傅里叶变换转换到频域，从而得到原始语音信号的频谱特性。为了更好地分析原始语音信号的频谱特性，并给出了原始语音信号频谱图的三维立体图，如图2所示。

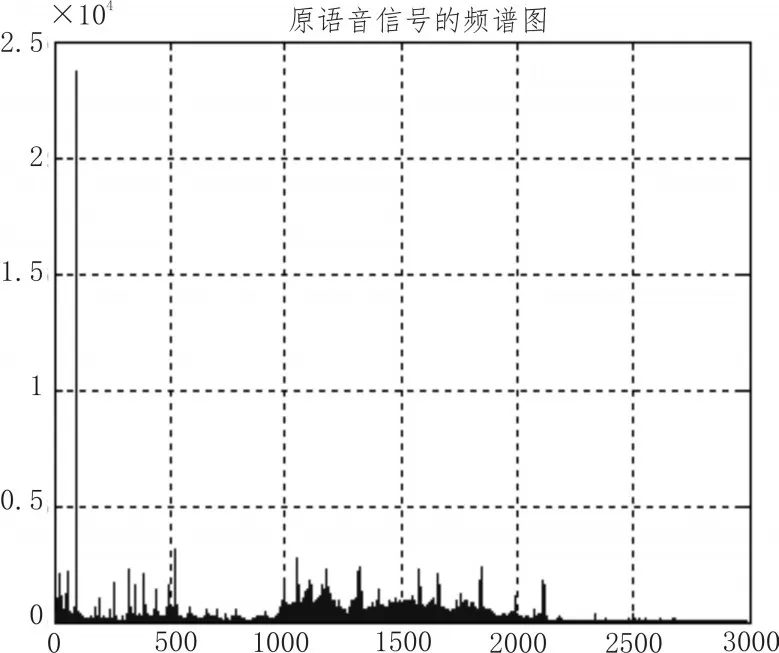
图2 原语音信号频域图

3）嵌入音频信号的时域及频域分析

将保存好的语音信“tonghuazhen.wav”文件在MATLAB软件中利用相关函数读出，如：

可得到嵌入语音信号的时域波形图如图3所示。

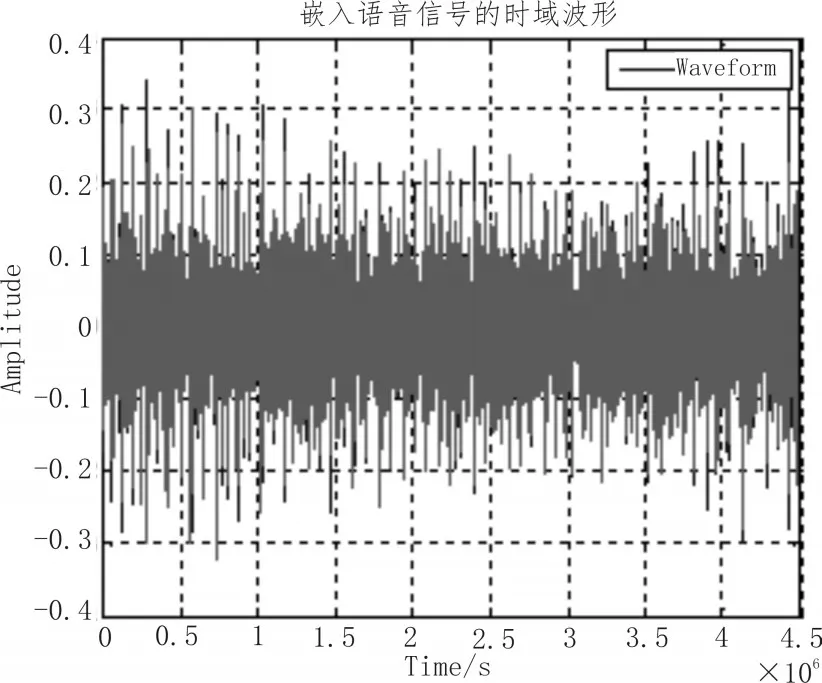
图3 嵌入语音信号时域图

画出嵌入语音信号“tonghuazhen”的时域波形图，对嵌入语音信号进行傅里叶变换转换到频域，可以得到嵌入语音信号的频谱特性。在MATLAB软件中运行相关程序如：

可得到嵌入语音信号的频谱图，如图4所示。

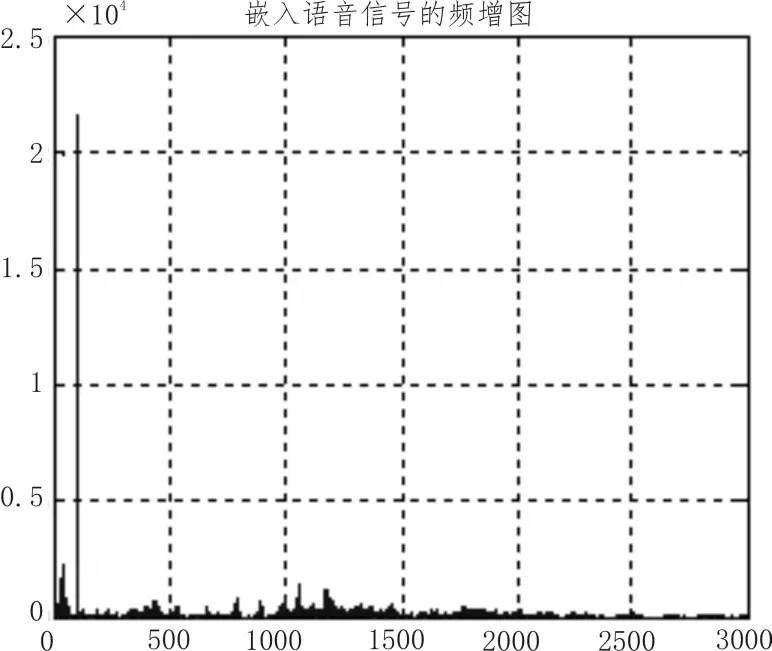
图4 嵌入语音信号频域图

4）加密语音信号时域及频域分析

将原始语音信号与倍乘后的嵌入语音信号相叠加后形成的语音信号。论文中采用的是嵌入语音信号的0.5倍。两段长度相同的语音信号能够直接相加，可是，两段程度不同的语音信号相互叠加，要利用resample函数实现语音信号的长度相等。

假设原始语音信号x的长度n1，嵌入语音信号y的长度为n2，且n1＞n2，有两种方法来处理：

方法一：将短信号y（长度为n2）重新采样成长度n1

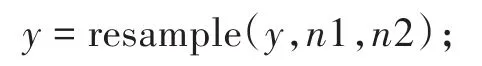
方式二：将长信号x（长度为n1）重新采样成长度n2

其中，x为原始语音信号，y为嵌入语音信号，alpha为相关系数，s为加密语音信号。用到的加密语音信号的主要函数及代码如下：

n1，n2分别为原始语音信号和嵌入语音信号的长度，回放叠加后的语音信号，会发现成功的将嵌入语音信号叠加到原始语音信号中，并且得到加密语音信号的时域波形图，如图5所示。

图5 加密语音信号时域图

画出加密语音信号的时域波形，对加密语音信号进行傅里叶变换转换到频域，得加密语音信号的频谱特性如图6所示。

5）数字音频信号的提取

数字音频信号的嵌入过程可以简单理解为音频的加密，那么相反的逆运算，数字音频信号的提取过程也可以理解为音频的解密，即恢复原始音频信号的过程。

将加密的信号进行相关处理，调用格式为：h=salpha*y；

其中，s为加密语音信号，alpha为相关系数，y为嵌入语音信号，h为恢复原始语音信号。

在MATLAB软件中运行有关音频信号的提取过程的程序代码，如：

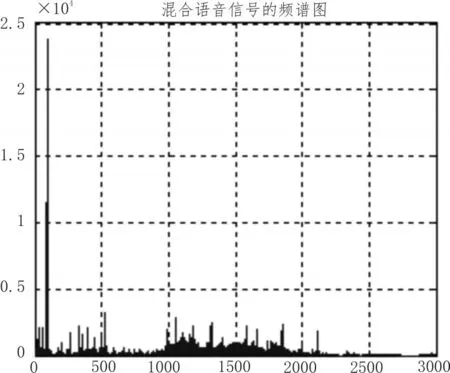
图6 加密语音信号频域图

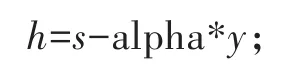
回放恢复后的语音信号，和原始语音信号相差不大，并且可得到恢复原始语音信号的时域波形图，如图7所示。

图7 恢复后语音信号时域图

做出解密后原始语音信hengdu.wav的时域波形图，然后对解密后的原始语音信号进行傅里叶变换转换到频域，可以得到解密后的原始语音信号的频谱特性。在MATLAB软件中运行相关程序如：

可得到恢复原始语音信号’chengdu.wav’的频谱图，为了更好地分析提取后的原始语音信号的频谱特性，并一道给出了提取后原始语音信号频谱图的三维立体图，如图8所示。

至此，利用MATLAB软件完成了数字语音信号的加密和解密过程，分析对比原始语音信号和恢复后的语音信号的异同，得出结论，阐明原因。

6）噪声信号的时域及频域分析

对原始语音信号进行抗噪性能分析，必须先人为构造一段随机高斯噪声信号，随机高斯噪声信号为：noise=0.005*randn（a，2）；即利用randn函数产生2列a行的随机高斯噪声，a为原始语音信号’chenhdu.wav’的长度。

在MATLAB软件中运用相关函数播放人为构造的随机高斯噪声并画出它的时域波形图及频谱图，运行有关随机高斯噪声的程序代码将会获得所加的随机高斯噪声的时域波形图和频谱图如图8所示。

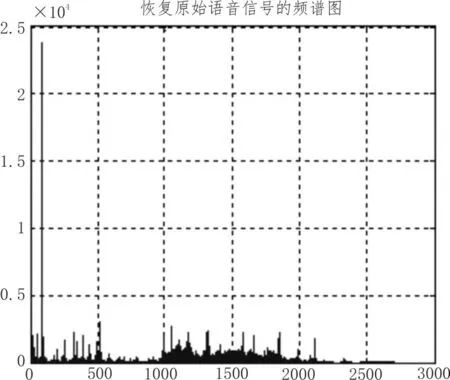
图8 恢复后语音信号频域图

由图9中的噪声信号的频谱图我们可以看出，所加的随机高斯噪声为高频噪声，且在整个区间都分布着，从回放的语音中，我们也可以清楚的听到所加的随机高斯噪声。

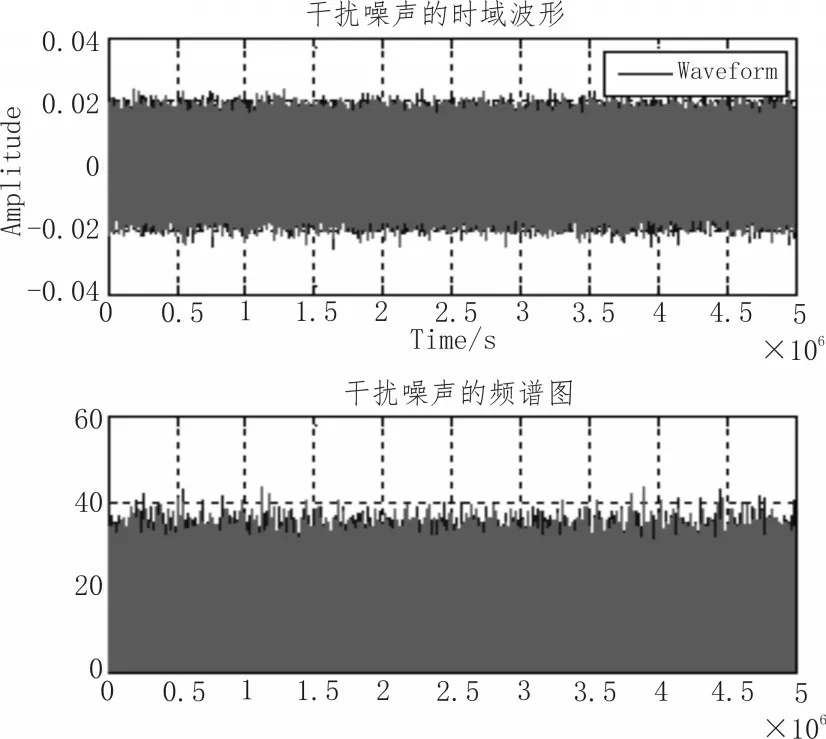
图9 噪声信号时域及频域图

在MATLAB软件中将原始语音信号与随机高斯噪声信号进行矩阵加法运算，并对经过加法运算的语音信号进行播放，利用plot有关函数进行绘制加噪语音信号的时域波形图，然后在MATLAB软件中能够运用函数FFT对语音信号进行快速傅里叶变换，继续对加入噪声后的语音信号进行频谱分析，绘制频谱图。

7）加噪语音信号的时域及频域分析

将原始语音信号x与人为构造的随机高斯噪声信号noise进行叠加，调用的形式为：w=x+noise；

公式中，w为加噪信号。

在MATLAB软件中实现在原始语音信号中加入构造的随机高斯噪声并绘制出加噪语音信号的时域波形图，播放加过随机高斯噪声后的声音信号。可以在MATLAB软件中运行有关程序代码如：

w=x+noise；

将会获得叠加噪声后的语音信号的时域波形图及频谱图如图9所示。

从回放的语音中我们可以听到原始语音信号以及所加的高斯噪声，从图10的时域波形图中可以看出噪声加入后时域波形都有明显的波形变化，对比原始语音信号和加噪后的语音信号可知，所构造的随机高斯噪声成功的叠加到了原语音信号上。

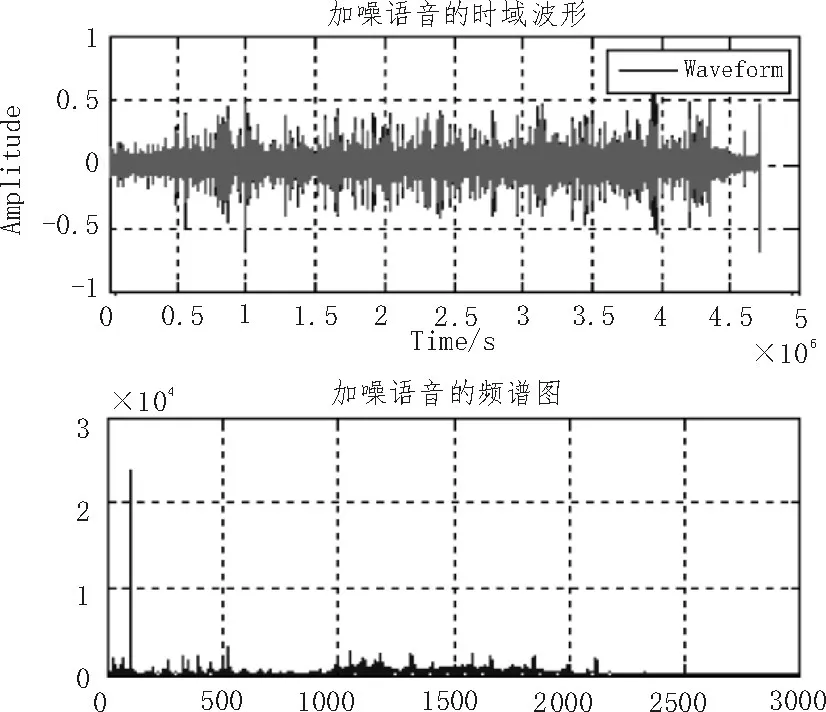
图10 加噪语音信号时域频域图

8）数字音频信号的去噪处理

对加入的噪信号进行逆运算，也就是把加噪语音信号与随机高斯噪声信号进行矩阵的减法运算，并对经过减法运算之后的语音信号进行回放，然后对去噪语音信号进行快速傅里叶变换并进行频谱分析，绘制频谱图。

将加噪语音信号w与随机高斯噪声语音信号noise进行矩阵减法运算，其调用的形式为：p=wnoise；

公式中，p代表的是去噪信号。

得到去噪语音信号的时域波形图及相应的频谱图如图11所示。从回放的语音中我们可以清楚的听到原始语音信号，从图11的时域波形图中可以看出明显的波形，对比原始语音信号和去噪后的语音信号可知，所构造的随机高斯噪声成功的脱离了加噪语音信号上，恢复了原始语音信号。

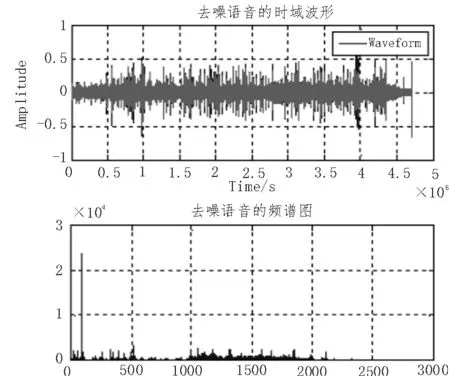
图11 去噪语音信号时域及频域图

3 结束语

对一段语音信号进行嵌入、提取、以及加噪处理，进而成功实现对数字音频信号的加密，通过对比加密前后的数字音频进行时域和频域的分析后，并通过听取声音的杂乱无章来辨别。经过算法的逆运算，成功的恢复原语音信号，恢复的信号与原始信号差别不大。将来根据需要在同一段音频信号中嵌入较多的密钥，使得信号恢复得更精准，从某种程度上提高了信息的安全性。