基于信号重构的伪随机跳频引信信号处理技术

涂友超，叶 涛,李 萌

(1.信阳师范学院 物理电子工程学院，河南 信阳 464000；2.信阳高级技工学校，河南 信阳 464000)

0 引言

在现代战争中，无线电引信对抗、通信对抗、雷达对抗和光电对抗，已成为电子对抗领域的重要组成部分[1-3].随着引信干扰技术的发展，无线电引信面临的战场电磁环境日益复杂，早期的无线电引信，如脉冲多普勒引信[4，5]、调频连续波引信[6]等，容易受到干扰而导致早炸和失效，在复杂的战场电磁环境中，如何有效地检测出目标回波信号、实时提取目标的距离和速度信息是伪随机跳频引信工程化的关键[7]. 文献[8]利用目标回波信号的频率、幅度和增幅速率三个特征量，提出了一种采用幅度检测、增幅速率检测和带外干扰信号检测的伪随机跳频引信信号处理方法，算法虽然具有严苛的判决条件，但该算法是建立在回波信号具有较高信噪比的基础上，当回波信号信噪比较低时，幅度检测和增幅速率检测都将失效，从而会严重影响引信的正常工作.文献[7]提出了一种基于匹配滤波的定距方法，算法虽然能够进行精确的定距处理，但当弹目间相对运动速度较大时，多普勒失配问题将严重影响伪随机跳频引信的定距功能.

为此，本文提出一种基于信号重构的伪随机跳频引信信号处理方法.该算法首先利用伪随机跳频引信的发射信号重构一组用于匹配滤波的本地参考信号，然后将这组信号分别与目标回波信号进行相干积累，其中任一通道相关值超过预设门限时，即可判定为伪随机跳频引信定距成功.

1 伪随机跳频引信工作原理

伪随机跳频引信原理框图如图1所示.在时序发生器的控制下，伪随机序列发生器产生一个伪随机序列作为选频码，控制频率合成器产生频率不断跳变的伪随机跳频信号，经功率放大器放大、匹配网络匹配后由发射天线辐射出去；接收天线接收到目标反射的回波信号后，经低噪声放大器放大后与本地载波信号混频，混频输出信号在同步系统的作用下由数字信号处理电路进行放大、匹配滤波处理，提取出目标距离信息和多普勒信息，当满足起爆条件时，执行级产生起爆信号.

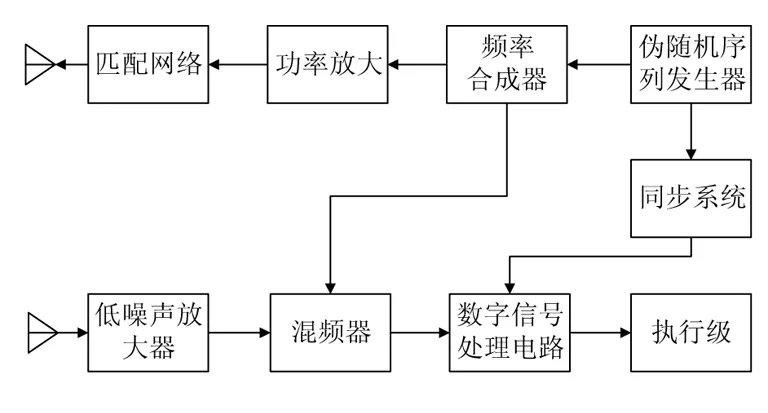
图1 伪随机跳频引信原理框图Fig. 1 Principle diagram of PRFH fuze

2 基于信号重构的伪随机跳频引信定距

伪随机跳频引信发射信号的表达式为

u(t)=cos(2π(f0+m(t)Δf)t).

(1)

式(1)中：f0为载波频率；Δf为跳频频率；m(t)为伪随机序列，可表示为

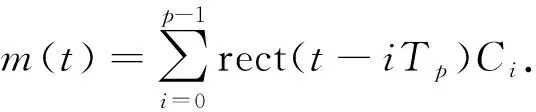
(2)

式(2)中:rect(·)为矩形窗，Tp为码元宽度，p为码长，{Ci}={+1,-1}为双极性二进制伪随机序列.

设短时间内弹目间相对运动状态为匀速直线运动，初始距离为R0，相对运动速度为v，由式(1)可知，目标回波信号为

ur(t)=cos(2π(f0+

(3)

式(3)中：R(t)=R0-vt为弹目间瞬时距离，c为电磁波传播速度.

式(3)可改写为

(4)

在对伪随机跳频引信信号处理之前，首先需将回波信号变换至基带信号.由于针对的是跳频这一特殊体制引信，其在进行基带变换时需进行两次混频操作.

一次混频本地参考信号为

s1(t)=cos(2πf0t)

.

(5)

将式(4)与式(5)相乘经低通滤波滤除高频分量后，即可得一次混频后的结果

(6)

二次混频参考信号为

s2(t)=cos(2πΔft).

(7)

将式(6)与式(7)相乘经低通滤波滤除高频分量后得到二次混频后的信号

(8)

由式(8)可以看出，当多普勒较小时，需积累多个伪随机序列才能准确测频，从而影响定距的实时性；另外，由于伪随机跳频信号是多普勒敏感信号，当多普勒失配时将严重影响引信的定距精度.

为此，本文提出了一种基于信号重构的伪随机跳频引信匹配滤波定距方法.首先利用本地伪随机序列重构一组用于匹配滤波的本地参考信号，重构示意图如图2所示.图2中，Δfd覆盖了目标回波信号多普勒可能存在的范围，若不进行多普勒估计，直接采用匹配滤波法会产生严重的定距误差.本文将多普勒范围Δfd划分为若干个小的多普勒区域，阈值分别为fd1、fd2、…、fdN，利用这些多普勒阈值重构一组用于匹配滤波的本地参考信号，可表示为

(9)

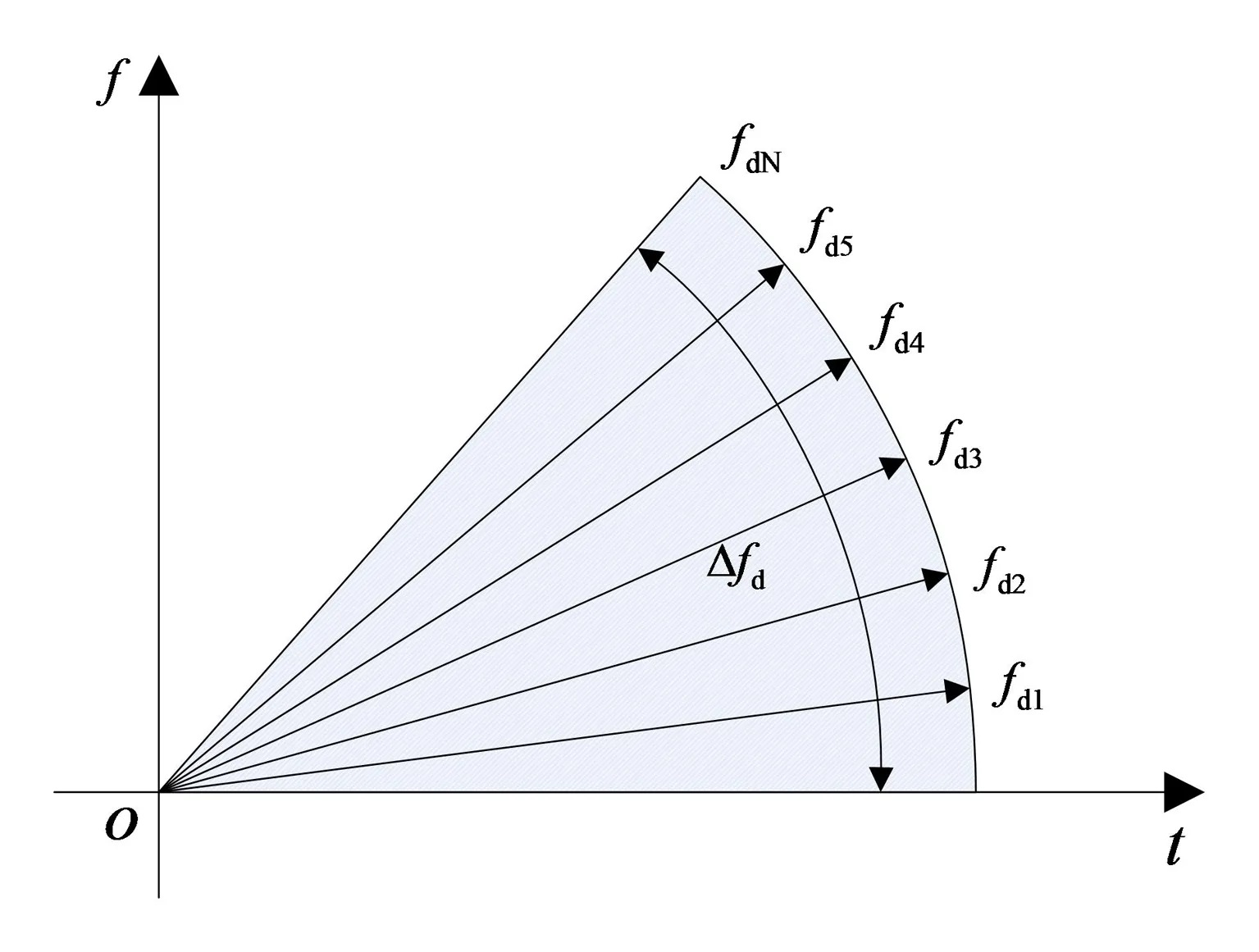
图2 信号重构示意图Fig. 2 Sketch diagram of signal reconstruction

将二次混频后的基带回波信号输入重构滤波器组的各通道进行匹配滤波，匹配滤波器组各通道输出结果为

fdi)(t-τ)))dt.

(10)

由于重构的滤波器组覆盖了目标回波信号多普勒可能存在的范围，因此，无论弹目间的瞬时速度如何，匹配滤波器组都会有一路输出将超过预设门限，从而实现对目标的精确定距，避免了多普勒失配导致定距误差大以及预设门限设置偏低引起的虚警概率升高等问题，增强了伪随机跳频引信的可靠性和抗干扰性能.

为更清楚的说明信号重构思想，本文进行了仿真分析.设弹目间相对速度v=0～1000 m/s，伪随机序列码长p=63，载波频率f0=3.3 GHz，跳频频率Δf=100 MHz，多普勒频率Δfd=0～22 kHz，将多普勒范围Δfd划分为7个小的多普勒区域，阈值fdn分别为1.65、4.95、8.25、11.55、14.85、18.15和21.45 kHz.目标回波信号与匹配滤波器组各通道相关峰值与多普勒频率之间的关系如图3所示.由图3可知，当预设启动门限为80 dB时，只要多普勒频率处于预设范围内，至少会有一个通道将超出启动门限，输出启动信号驱动执行级.若不进行多普勒估计，本地直接采用伪随机序列与回波信号相关，需设置启动门限为30 dB左右，这将大大增加伪随机跳频引信的虚警概率，削弱引信的可靠性和抗干扰性能.

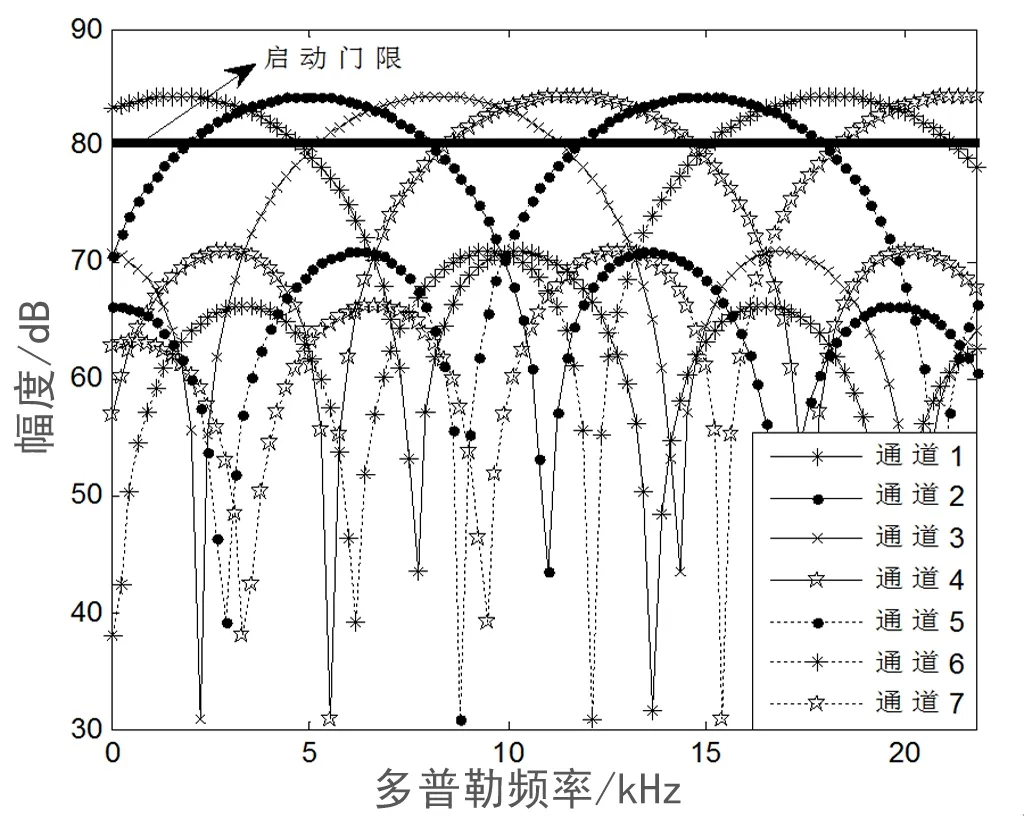
图3 相关峰值与多普勒关系图Fig. 3 Relationship between output maximumsDoppler frequency

3 实验验证及测量结果

为进一步说明本文定距方法的可行性，选取一点目标对伪随机跳频引信的定距原理进行仿真分析，仿真参数如表1所示.多普勒阈值的设置和前一节一致.

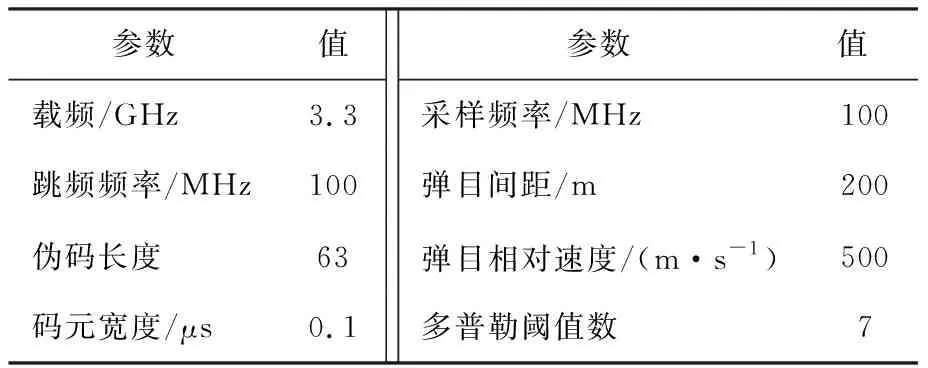
表1 仿真参数Tab. 1 Simulation parameters

接收到的目标回波信号经二次混频后的基带信号时域波形和频谱如图4所示.由图4可知，由于跳频频率的存在，基带回波信号中含有两个多普勒信号,另外由于伪随机跳频引信频率随机跳变，敌方很难通过捕获信号频率的方式来实施干扰，因此该体制引信本身具备强的抗干扰、抗截获能力.

图4 基带回波信号及其频谱Fig. 4 Based-band eco and its frequency spectrum

将二次混频后的基带回波信号输入至本文重构的匹配滤波器组，各通道输出结果以及采用原始相关定距法定距结果分别如图5所示.设启动门限为80 dB，如图中红线所示，只有通道4将输出起爆信号，其他各通道由于多普勒失配问题，相关峰值较小，均未能产生起爆信号.因此，采用本文方法在完成定距的同时，还可粗略估计目标回波信号的多普勒频率为11.55 kHz，与实际的11 kHz有略微差别.同理，原始相关定距法由于多普勒失配问题也未能产生起爆信号，发现概率较低，引信可靠性差.若将引信启动门限降低，虽然会提高引信的发现概率，但同时也大大提高了其虚警概率，特别在噪声较大时更为明显.

图5 本文定距法与原始相关定距法结果图Fig. 5 Fixed distance results of method proposed in this paper and traditional method

图6为信噪比为15 dB时，本文定距方法与原始相关定距法的结果图.从图中可以明显看出，该信噪比条件下，原始相关定距法已经基本失效，而本文定距方法通道4依然可以输出对应的起爆信号，因此本文提出的基于信号重构的定距方法具有更高的可靠性及更强的抗干扰能力.

图6 信噪比为-15 dB时本文定距法与原始相关定距法结果图Fig. 6 Fixed distance results of method proposed in this paper and traditional method whenSNR=-15dB

4 结论

本文提出的伪随机跳频引信信号处理方法能够对目标区域进行精确探测，有效地解决了传统相关定距法中多普勒失配引起的定距精度差、虚警概率高等问题；另外，该算法无须进行任何回波信号参数估计，算法简单易于工程实现.该研究成果在目标探测与识别、精确制导等领域中具有应用价值.