具非瞬时脉冲收获单种群动力学模型的控制阈值研究

焦建军，李利梅,刘兰兰，聂星屹

(贵州财经大学 a.数学与统计学院;b.继续教育学院，贵州 贵阳 550004)

0 引言

许多生命现象可以用动力学建模的方法来建立相应的数学模型，通过研究这类数学模型来进一步研究生物动力学问题,以使人们对生态学乃至生命科学有更加深入的了解.近年来，人们发现许多生命现象的发生以及人们对生命现象的优化控制，并非一个连续的过程，不能单纯地用微分方程与差分方程来描述.周期的脉冲微分方程在生命科学中的应用[1],开始于医药科学，研究药物在人体中的二分部，口服、注射药物常常是以脉冲形式使药物进入人体的，因此描述药物在人体(包括血液、脏器、肌肉等)中浓度变化情况，应用周期脉冲微分方程则显得更为合理；研究癌细胞的化疗中，癌细胞组织的变化过程也是类似的，因为打针、吃药、化疗都是周期的脉冲行为；研究传染病的防疫，进行免疫接种方式的过程中，发现免疫接种方式也是一种周期性的脉冲行为.周期脉冲微分方程的另一类应用包括可再生资源的开发与害虫的综合治理.可再生资源开发，也常常是周期性的脉冲行为;在农业害虫治理过程中，实施农药、投放天敌也常常是周期性脉冲行为.同时许多学者运用了脉冲微分方程理论来研究种群脉冲出生与收获、传染病的控制、淡水生态系统的管理、人体血糖的控制等问题[2-9]，为现实的生物资源管理提供了可靠的策略依据.

焦建军等[2]研究了具脉冲出生与脉冲收获阶段结构单种群动力学模型：

(1)

其中:x1(t) 和x2(t)分别表示种群幼体与成体的密度；a>0 表示种群的脉冲出生系数；d1>0表示种群幼体的死亡系数；c>0表示种群幼体向成体转化的系数；d2>0表示种群成体的死亡系数； 在t=(n+l)τ时刻对种群成体进行脉冲收获； 在t=(n+1)τ时刻种群脉冲出生；μ表示种群成体的收获系数，且0<μ<1；τ表示种群的脉冲出生周期，也就是种群成体的收获周期. 考虑到实际上种群幼体的死亡率比种群成体死亡率大，所以可以假设d1>d2.

而事实上，种群的出生应当包含着瞬时脉冲收获时刻与非瞬时脉冲收获区间，很少有人研究具有非瞬时脉冲收获的种群动力学模型行为.

1 模型的建立

考虑种群是脉冲收获且其包含瞬时脉冲收获与在接下来的某个时间段上的非瞬时脉冲收获，建立具非瞬时脉冲收获单种群动力学模型：

(2)

其中:x(t)表示种群在时刻t的密度，种群在区间(nτ,(n+l)τ]上是Logistic增长，a>0表示种群在区间(nτ,(n+l)τ]上的内禀增长率，b>0表示种群在区间(nτ,(n+l)τ]上的种内竞争系数.μ>0表示种群在瞬时脉冲收获时刻t=(n+l)τ的收获系数，d>0表示在区间((n+l)τ,(n+1)τ]内种群的非瞬时脉冲收获系数，lτ是种群的非脉冲收获区间长度，(1-l)τ是种群非瞬时脉冲收获区间长度(00表示种群脉冲收获周期.种群密度函数x(t)在时刻t=(n+1)τ是连续的.

考虑到种群的非瞬时脉冲出生，假设l→1且l≠1.

2 动力学分析

假设x(t)是系统(2)的解, 它是一个分段连续函数X:R+→R+,X(t)在区间(nτ,(n+l)τ]与((n+l)τ,(n+1)τ]上是连续的,并且

与

是存在的，显然,系统(2)的右边函数的光滑性保证了其解的全局存在和唯一性[1].

由系统(2)的第一与第三个方程,容易得到系统(2)在脉冲点之间的解析解为：

x(t)=

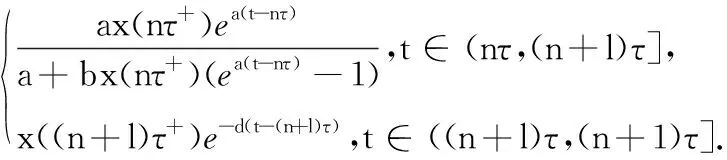
(3)

由系统(2)的第二与第四个方程,得到系统(2)的频闪映射为：

(4)

方程(4)有两个不动点F1(0)与F2(x*), 其中

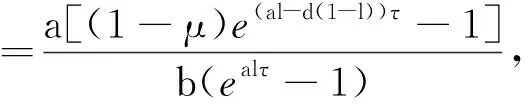
(1-μ)e(al-d(1-l))τ>1.

(5)

定理1 i)当 (1-μ)e(al-d(1-l))τ<1时，方程(4)的唯一零不动点F1(0)是全局渐近稳定的.

ii)当(1-μ)e(al-d(1-l))τ>1时，方程(4)的零不动点F1(0)是不稳定的, 方程(4)的正不动点F2(x*)是全局渐近稳定的，其中x*如方程(5)所定义.

证明为了方便，引入记号xn=x(nτ+),那么差分方程(4)可以写成

xn+1=F(xn),

(6)

其中

B=b(ealτ-1).

i) 当(1-μ)e(al-d(1-l))τ<1时，方程(6)有唯一的不动点F1(0)，于是

(1+μ)e(al-d(1-l))τ<1.

(7)

所以方程(6)的唯一不动点F1(0)是局部渐近稳定的，进而是全局渐近稳定的.

ii) 当(1-μ)e(al-d(1-l))τ>1时，对于方程(6)的不动点F1(0)，于是

(1-μ)e(al-d(1-l))τ>1.

所以方程(6)的不动点F1(0)是不稳定的.

当(1-μ)e(al-d(1-l))τ>1时，对于方程(6)的不动点F2(x*)，于是

所以方程(6)的不动点F2(x*)是局部渐近稳定的，进而是全局渐近稳定的.证毕.

由定理1易得：

定理2 i)当(1-μ)e(al-d(1-l))τ<1时，系统(2)的平凡周期解是全局渐近稳定的.

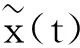
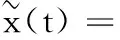
(8)

其中:x**=(1+μ)e-dlτx*,x*如方程(5)所定义.

3 讨论

根据生物资源管理的实际，讨论了具非瞬时脉冲收获的单种群动力学模型，得到了生物资源管理的控制阈值的充分条件.由定理2可知，对于具非瞬时脉冲收获的单种群动力学模型，得到了种群初次脉冲收获的阈值

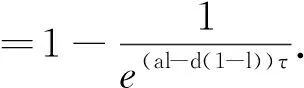
当μ>μ*时，系统(2)的种群灭绝，当μ<μ*时，系统(2)的种群持续生存.说明了种群的初次收获量对于系统的持久起着重要的作用.同时，也可以得到非瞬时脉冲出生区间系数l存在阈值：

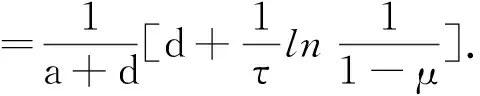
当(1-l)τ>(1-l*)τ时，种群灭绝，当(1-l)τ<(1-l*)τ时，种群持续生存.该结论也表明种群非瞬时脉冲收获区间的长短对于种群的持续生存具有重要的作用. 从上面的讨论我们猜想对于某些濒临灭绝的有一定经济价值的生物是可以适当减少其初次脉冲收获量或者是缩短其非瞬时脉冲收获区间的长度，从而保护该物种持久生存.