基于ORB特征点的多目标匹配

高建哲，吕文阁

0 引言

图像匹配是机器视觉中一种常用的图像处理和图像分析技术。广泛应用于军事和民用生活领域，例如目标跟踪、车辆监测、卫星导航、机器人控制以及工业检测等。其主要方法有基于灰度值的匹配，基于轮廓边缘的匹配以及基于特征点的匹配，这些年来基于特征点的图像匹配方法已经成为国内外研究的热点。其中David G.Lowe提出了SIFT算法[1]，Herbert Bay等人提出了SURF算法[2]，不同的图像匹配算法在检测关键点和提取描述向量时采用不同的方法，构造出的局部特征描述子就会具有不同的鲁棒性，针对SIFT和SURF速度上的劣势，ERublee等人在2011年提出来一种快速局部特征检测算子ORB（oriented FAST and rotated BRIEF），该算子兼顾了SIFT和SURF的准确性和鲁棒性，同时又有较快的速度[3]。

在目标识别中，有时图像中存在待识别目标的多个相同或相似的副本，此时，不能够直接地使用特征点匹配算法，而是需要先分离多目标，然后对单一目标做出估计。因为在求解模板到目标的仿射变换参数时，其他的目标特征点会被认为是误匹配点，所以如何的分离这些特征点成为解决基于特征点的多目标匹配的关键。

对此，国内外的学者有着不同的研究，Lowe D等人利用Hough变换通过对特征点的可能的姿态进行投票分析，根据投票的峰值进行特征点的分类，但是计算繁琐比较费时[4]。吕冀等人通过为所有的匹配点建立统一的超定线性方程组并对其简化得到增广矩阵，然后对增广矩阵进行线性变换，从中提取多目标稳定的特征点，进而分离多目标特征点，但是鲁棒性有所欠缺[5]。朱迪等人通过对模板中心点在目标图像的估计，利用K-means进行中心点分类，进而分离多个目标，对于不确定目标个数的检测具有一定的局限性[6]。

因此，本文提出了一种基于ORB特征点和采用基于特征点密度峰值的聚类分析方法［7］进行模板中心的自适应判断，可以避免目标个数不确定时所带来的的问题，同时实验也验证了算法的快速性，稳定性，具有一定的应用的价值。

1 ORB特征点匹配

1.1 ORB特征点检测

ORB算子采用了FAST特征点和BRIEF描述子并加以改进。因为FAST特征点和BRIEF描述子均具有良好的鲁棒性，所以ORB算子也具有良好的鲁棒性。FAST特征点本身不具备旋转不变性，在ORB的方案中，为了解决这个问题，ORB定义了邻域矩如式(1)，通过矩计算来获取特征点的邻域的灰度强度质心，以特征点中心到灰度强度质心的方向作为FAST主方向。

其中，其中（x，y）是相对FAST特征点的位置，r为圆形邻域半径，一般取3或4，（x，y）∈ [-r，r]，I表示（x，y）坐标上图片的灰度值，mpq称为特征点（p+q）阶矩(p，q=0，1，2，…)。至此得到了FAST角点圆形邻域的强度中心点，其计算公式如下(2):

设特征点的中心为O，构造从特征点中心到灰度质心C的向量OC，作为特征点的方向，即FAST特征点的方向。因此，该角点的主方向角θ为式(3)：

这样FAST改进成了Oriented-Fast。ORB在特征描述方面，采用BRIEF描述子，BRIEF是一种快速的二进制特征描述算子，BRIEF描述子通过在图像上某点p的邻域内的随机选取n个点对，对于每一个点对可以形成一个二值测试τ来提取，其定义如式(4)。

其中，I（p，x）为p的邻域内x点处的像素灰度值，I（p，y）为p的邻域内y点处的像素灰度值，n一般取值为256，于是BRIEF特征描述子定义为如下式(5)。因此，BRIEF描述子本质上就是由这n个测试得到的n个字符组成的一个位字符串。

然而BREIF特征描述子在发生旋转时无法保持稳定，因此，将角点的主方向作为描述子的主方向，从而取得对旋转变化的鲁棒性。原理如下：设(xi,yi)为任意的参与二值测试的点对，则所有的点对可以定义一个2×n的矩阵如下式(6)：

于是利用特征点的主方向为θ的旋转矩阵Rθ就可以构造S的有向的形式Sθ=RθS。其中Rθ定义如下式(7)，θ为逆时针方向。因此得到了steered BRIEF为式(8)：

由此，ORB具有了旋转不变性的特点。

1.2 特征点匹配

由上节得到的特征点描述子的形式为二进制码串的形式，因此采用Hamming距离进行匹配，匹配点的hamming距离与非匹配点的hamming距离有较大的差异。匹配的相似度越高则hamming距离越小，因此，通过设定阈值的方式筛选正确的匹配点。如图1是特征点匹配示意图。

图1 ORB特征点匹配对

2 特征点分离

2.1 匹配点在目标图像上的中心估计

模板图的特征点集为T，目标图像的特征点集为S，（t，s）为模板图和目标图的一个匹配点对，其中t∈T，s∈S。记录模板特征点相对于模板中心的位置，模板中心c可以选取模板图像的几何中心点。模板特征点到模板中心的相对向量记为式(9)：

其中，p（c）为模板中心的位置坐标， p(ti)为某一个模板特征点的位置坐标。对于匹配正确的点对(ti,si)，则可以通过t，s的位置坐标以及特征点方向来近似的估计S的中心点cs

式中θ=θs-θt。θs为目标图像特征点的角度，θt为对应模板图像特征点的角度方向。每个具有匹配对目标图像的特征点对都会产生一个估计中心点。效果如图2所示，图2（a）为模板及其中心，图2（b）为目标图及其估计的中心点。

图2 估计中心点

2.2 中心点聚类分析

理论上，同一个目标副本所有特征点估计的中心点的坐标应该为同一个点，实际中，由于图像采集以及设备误差，因此中心点为距离靠的很近的点群，这些点位于实际中心点的某一邻域内。本文采用机器学习中的基于快速查找密度峰值的聚类算法来分离这些特征点。

式中dc为截止距离。对于dc的选取参考文献[8]。dij=dist（pi，pj）表示数据点pi，pj之间的某种距离，本文选取欧式距离。当 ρi为最大时， δi=max( )dij。

该算法认为聚类中心同时拥有以下两个特点：

（1）本身的密度足够大，即周围的点的密度均不超过它自己；

（2）和另外的聚类中心的距离相对来说更大。

图3 中心的点的分类

2.3 分类匹配

由于每一个中心点对应一个特征点，因此分类后的中心点等同于分类后的特征点，分别采用改进的随机一致抽样方法进行匹配筛选，获取模板到目标副本的变换矩阵，分离结果如图4所示。

图4 分离结果图

2.4 总体流程

从模板和待检测图像分别提取ORB特征点，采用Hamming距离进行初步的筛选匹配点对，然后利用模板图像特征点和模板中心形成的向量进行搜索图中心点的估计，接着采用基于密度峰的聚类方法进行搜索图的特征点的分类，同时可以去除一部分误匹配点，然后对分类后的点集分别采用随机一致抽样方法进行变换矩阵的求解，获取转换关系，得到模板在待检测图的位置以及旋转角度等信息。总体流程图如图5所示。

图5 总体流程图

3 实验结果

本实验程序是在opencv2.4.9和VS2013的基础上编写而成的，实验分为三部分，分别验证目标副本的个数能否自适应判断，该算法的鲁棒性，以及运行速度。

3.1 目标个数的自适应判断

如图6所示，左上图为模板图像，剩下的分别为目标为1，2，3，4，5个的情况，该算法均能够很好地判断出来目标的个数。

3.2 鲁棒性检测

鲁棒性检测主要是检测算法在遮挡，光照不均等，外部环境有差异的情况下的工作的稳定性，如图7所示，该算法在有待检测目标物体有重叠的情况下依然可以识别判断目标个数。

3.3 速度检测

本实验的硬件测试平台为Inter Core i5双核处理器，主频2.5 GHz，运行内存4 GB，本次实验选取十组图片（640×480）进行处理，分别与采用SIFT特征点以及SURF特征点的模板匹配定位进行比较。本文的处理算法速度平均为213.66 ms，是SIFT的3.2倍，是SURF的5.9倍。结果如表1所示。

图6 不同数目样本判断结果图

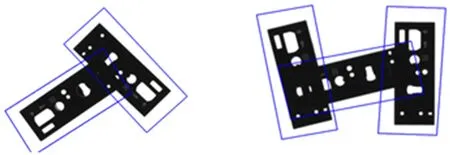
图7 在有遮挡重叠的情况下检测结果

表1 算法运行时间

4 结束语

针对特征点匹配的目标副本自适应个数匹配的问题，本文提出了一种基于ORB特征点和密度峰聚类的自适应判断目标副本个数的多目标匹配方法，运行速度较快，并且对于遮挡、重叠等具有一定的鲁棒性，在理论和应用上都具备一定的价值。