家用燃气灶热工性能测量及不确定度评定*
胡伟健,李志宏
0 引言
家用燃气灶作为我国家庭中普及率最高的一种厨房加热器具,其热工性能(热负荷和热效率)越来越受到消费者的重视。2008年5月1日开始实施的GB16410-2007要求嵌入式灶热效率大于等于50%,台式灶大于等于55%,同时规定,热负荷偏差应该在±10%以内。而最新版本的GB16410—201X《家用燃气灶具》(征求意见稿)则要求嵌入式灶热效率大于等于55%,台式灶大于等于58%,同时规定,热负荷偏差应该在±10%以内。
2012年12月3日,国家质量监督检验检疫总局发布《测量不确定度评定与表示》(GUM法)(JJF1059.1-2012)代替JJF1059-1999。2012年12月21日发布《用蒙特卡洛法评定测量不确定度》(JJF1059.2-2012),将蒙特卡洛法作为对GUM法的重要补充。根据我国《测量不确定度政策》的规定,检测实验室应有能力对每一项有数值要求的测量结果进行测量不确定度评定。当不确定度与检测结果的有效性或应用有关、当测试方法中有规定时和认可委员会有要求时,检测报告必须提供测量结果的不确定度[1]。
热负荷和热效率作为家用燃气灶热性能的重要指标,有必要对其测量结果进行不确定度评定。由于其测量模型比较复杂,且为非线性,采用GUM法评定不确定度,所求偏导比较困难,于是基于蒙特卡洛法的不确定度评定是有效的代替方法。
1 用蒙特卡洛法评定测量不确定度
1.1 蒙特卡洛法简介
蒙特卡洛法主要是用相关函数产生服从相应概率分布的随机数对各个输入量进行多次随机抽样,然后再进行概率分布传播,最后得到输出量的模拟结果,所以只要试验次数足够大,最后的模拟结果便近似于事件发生的概率,便可估计输出量的有关特征量。近年来,该方法被广泛的应用于测量不确定度的评定,其核心是求取模拟样本的标准差。其依据是分布传播,即能够通过输入量的概率分布确定输出量的概率分布。图1是概率分布传递的示意图。求解步骤按照用蒙特卡洛法评定测量不确定度[2-4]。

图1 3个独立的输入量的概率分布传递示意图Fig.1 Illustration of propagation of probability distributions for 3 independent input quantities
1.2 家用燃气灶热负荷测量不确定度评定示例
(1)测量原理和测量模型
热负荷是指低热值与燃气流量的乘积。本次试验选用某燃气灶能效及综合性能测试台对三种不同品牌的三个家用燃气灶(12T)的左炉(分别标记为1、2、3号灶)进行热负荷对比测试。如图2所示,将燃气灶与测试平台连接。燃气通过阀门流经湿式气体流量计,最后到燃气灶。其中湿式气体流量计的燃气流量、燃气温度、燃气静压力以及大气压力等参数是通过测试平台的传感器采集,并进行自动计算,最后将结果呈现在测试平台的屏幕上的。测试按照GB30720—2014《家用燃气灶具能效限定值及能效等级》[5]中的步骤进行。

图2 热负荷测量原理示意图Fig.2 Heat load measuring principlediagram
实测热负荷用公式(1)计算:

φ实—实测热负荷,单位为千瓦(kW);
Q1—15℃、101.3 kPa状态下试验燃气的低热值,单位为兆焦耳每立方米(MJ/m3);
V—测试耗气量,单位为L;
tg—燃气流量计内的燃气温度,单位为摄氏度(℃);
Pamb—试验时的大气压力,单位为千帕(kPa);
Pm——实测燃气流量计内的燃气相对静压力,单位为千帕(kPa);
S——温度为tg时的饱和水蒸气压力,单位为千帕(kPa)(当使用干式流量计测量时,S值应乘以试验燃气的相对湿度进行修正);
t——试验时间,单位秒(s)。
(2)测量数据
对三个家用燃气灶的各个输入量分别进行10次独立测量,计算得到输入量的试验标准差如表1。

表1 1、2、3号灶热负荷各输入量结果数据表Table1 Datasheet of heat input for 1,2 and 3 stoves
其中耗气量V为10,是一个固定值,这样只要记录对应时间就可以求得燃气流量。天然气的低热值Q1根据GBT11062-2014中低热值体积发热量的计算方法计算,本次试验所用天然气成分为甲烷含量≥99%,乙烷含量≤0.6%,空气含量≤0.4%,具体计算过程如下:
已知组成混合物,在燃烧温度t1,计量温度t2和压力p2时的理想气体体积发热量用公式(2)

式 Hˉ∘(t1)为混合物的理想摩尔发热量可查GB/T 11062-2014表3获得; R为摩尔气体常数(8.31451 J.mol-1.K-1);T2为绝对温度(T2=t1+273.15)。
当乙烷含量为0.6%,空气含量为0,甲烷含量为99.4%时低热值取上限

当乙烷含量为0,空气含量为0.4%,甲烷含量为99.6%时低热值取下限,

因此天然气低热值的取值范围为[33.80,34.10],根据最大熵原理[6-7],天然气低热值为均匀分布,因此可以取值其最大允许误差为±0.15,则其标准不确定度为
(3)A类测量不确定度评定
将前两次测量值的均值作为测量结果时,则A类测量不确定度为u(x)=。结果如表2所示。

表2 1、2、3号灶热负荷各输入量的标准不确定度Table2 Standard uncertainty of heat input for 1,2 and 3 stoves
(4)分布传递的结果
由最大熵原理可以求得各个输入量均为正态分布。当把前两次测量值的均值作为测量结果时,采用蒙特卡洛法传递概率分布[8-11],利用MATLAB软件进行计算。1、2、3号灶的运行结果如表3所示,输出量Y也即实测热负荷的概率分布如图3所示。取三个灶扩展不确定度的平均值作为本套设备热负荷测量不确定度的最终值,即为0.76%。
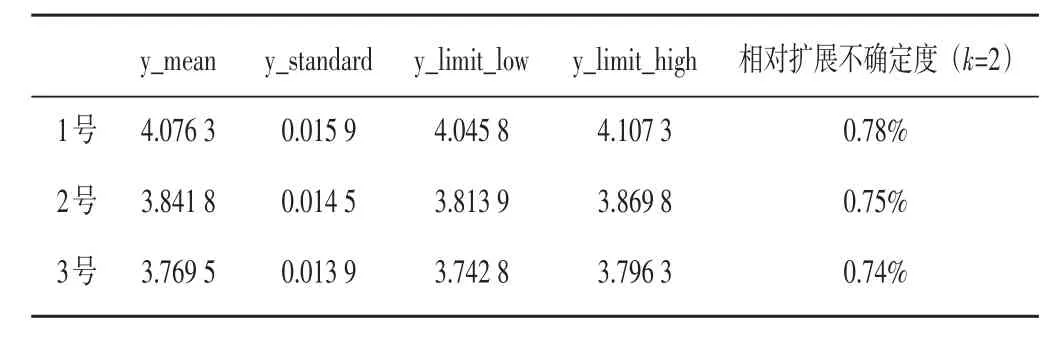
表3 1、2、3号灶热负荷的不确定度Table3 Uncertainty of heat load for 1,2 and 3 stoves
1.3 家用燃气灶热效率测量不确定度评定示例
(1)测量原理和测量模型
热效率是指系统有效输出的能量与输入的能量之比。同理对三个燃气灶进行热效率试验,测试步骤按照GB30720-2014《家用燃气灶具能效限定值及能效等级》中热效率试验方法进行。由式(3)计算实测热效率。

M——实际加水量与铝锅换算为当量加水量之和,单位为千克(kg);
M1——加入锅内的水质量,单位为千克(kg);
M2——铝锅的质量(含盖子和搅拌器),单位为千克(kg);
试验完上限锅和下限锅的实测热效率后用式(5)计算总热效率。

η——灶头总热效率,%;
η实,下——使用下限锅时的实测热效率,%;
η实,上——使用上限锅时的实测热效率,%;
q下——使用下限锅试验时的锅底热强度,单位为瓦每平方厘米(W/cm2);
q上——使用上限锅试验时的锅底热强度,单位为瓦每平方厘米(W/cm2);
注:锅底热强度等于实测热负荷(W)/试验用锅在正投影面的面积(cm2)。
根据式(5),热效率η的输入量有实测热效率η实和锅底热强度q,而实测热负荷又是锅底热强度q的输入量。因此,可以分别评定实测热效率和实测热负荷的不确定度,以其作为输入量,再评定燃烧器热效率的测量不确定度,则式(5)就可以作为燃烧器热效率的数学模型。

图3 1、2、3号灶热负荷概率分布图Fig.3 Probability distribution of heat load for 1,2 and 3 stoves
(2)测量数据
同理对三台灶的各个输入量进行10次独立测量,计算得到输入量的试验标准差如表4和表5所示。

表4 三个灶的下限锅热效率各输入量数据Table4 Theinput dataof thermal efficiency of lower limit

表5 三个灶的上限锅热效率各输入量数据Table5 Theinput dataof thermal efficiency of upper limit
(3)A类不确定度评定
同理将前两次测量值的平均值作为测量结果,可以得出三个灶的下限锅和上限锅热效率各输入量的标准不确定度。结果如表6和表7所示。

表6 下限锅热效率各输入量的标准不确定度Table 6 The standard uncertainty of each input quantity of lower pot thermal efficiency

表7 上限锅热效率各输入量的标准不确定度Table 7 The standard uncertainty of each input quantity of theupper pot heat efficiency
(4)分布传递结果
将两次测量值的平均值作为测量结果,采用蒙特卡洛法传递概率分布,利用MATLAB软件进行计算,则三个灶的总的实测热效率的概率分布如图4所示,总热效率的计算结果如表8所示。

表8 三个灶两次测量的热效率的不确定度Table8 Uncertainty in thermal efficiency of threefocifor twomeasurements
2 用GUM法评定测量不确定度
2.1 1号灶实测热负荷的GUM法评定
根据实测热负荷的模型和不确定度传递率,取两次测量的平均值作为测量结果时,合成标准不确定度的公式如式(6)所示。


图4 三个灶总实测热效率概率分布图Fig.4 Probability distribution of total measured thermal efficiency of threestoves
其中,

将数据代入式(6)得:

2.2 1号灶实测热效率的GUM法评定
根据实测热效率的模型和不确定度传递率,取两次测量的平均值作为测量结果时,上限锅合成标准不确定度的公式如式(7)所示:

其中,
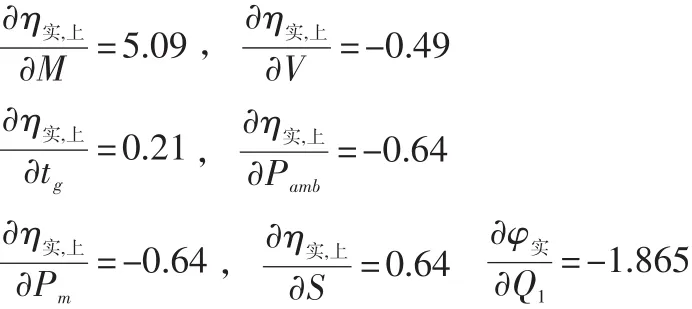
代入式(7)得 uc(η实,上)=0.2653。
同理,下限锅实测热效率的合成标准不确定度公式为:
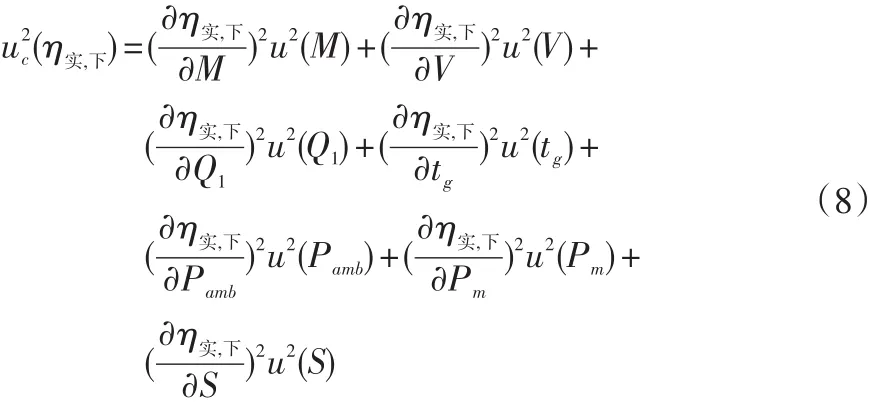
其中,

代入式 (8) 得 uc(η实,下)=0.261 0 。
于是,总的热效率的合成标准不确定度公式为:

代入式(9)得uc(η)=0.1996,则其相对扩展不确定度为×100%×2=0.66%,同理可以求得其他两个灶的相对扩展不确定度分别为0.83%、0.73%。
3 MCM和GUM的比较
综上所述,热负荷MCM和GUM计算的结果如表9所示;热效率MCM和GUM计算的结果如表10所示。可以看出两者结果是一致的。

表9 三个灶热负荷MCM和GUM结果统计表Table9 Threeheat load MCMand GUMstatistical tables
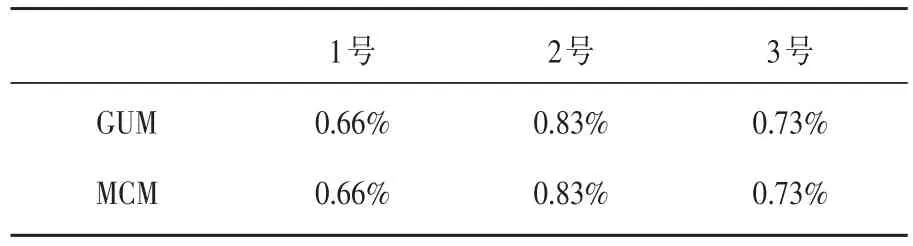
表10 三个灶的总热效率MCM和GUM结果统计表Table 10 The total thermal efficiency of three foci MCM and GUM resultstable
4 结论
用蒙特卡洛法进行概率分布传递,最后实测热负荷和总热效率的模拟结果为正态分布。
用GUM法和MCM法两种方法评定的热负荷和热效率的不确定度结果一致。
在GUM法的评定过程中可知试验时间的测量不确定度对热负荷测量结果不确定度的影响最大;当量加水量的测量不确定度对热效率测量结果不确定度的影响最大。
将三个灶用MCM法评定热负荷的不确定度的平均值作为本套设备的最终不确定度,结果为0.76%,热效率的最终不确定度为0.74%。

