一种基于决策树ID3的改进算法

王子京 刘毓

摘 要： 针对传统ID3算法无法处理属性值连续的数据集，设计了一种新的改进算法用于连续评价数据的处理。改进算法先用聚类算法对连续属性值进行离散化，再计算属性的粗糙度作为属性分裂的标准，最后用改进的ID3算法生成决策树。通过仿真验证了该方法的预测正确率，并探讨其应用条件。实验结果表明，在不降低正确率的情况下，该算法可处理属性值连续的数据且具有更好的可读性及更低的运算量。

关键词： 数据挖掘； 决策树； 粗糙集； ID3算法； 大数据； 算法改进

中图分类号： TN911.1?34； TP181 文献标识码： A 文章编号： 1004?373X（2018）15?0039?04

An improved ID3 algorithm for decision tree

WANG Zijing， LIU Yu

（School of Communications and Information Engineering， Xian University of Posts & Telecommunications， Xian 710121， China）

Abstract： The traditional ID3 algorithm can′t process the dataset with continuous attribute value. Therefore， an improved ID3 algorithm is designed to process the continuous evaluation data. The clustering algorithm is used in the improved algorithm to discrete the continuous attribute values， and then the roughness of the attribute is calculated as the divisive standard of the attribute. The improved ID3 algorithm is adopted to generate the decision tree. The prediction accuracy of the method is verified with simulation， and its application condition is discussed. The experimental result shows that the improved algorithm can process the data with continuous attribute value， and has high readability and less computational amount while maintaining the accuracy.

Keywords： data mining； decision tree； rough set； ID3 algorithm； big data； algorithm improvement

0 引 言

ID3算法是数据挖掘中一个重要的分类算法[1]，该算法用信息增益作为分裂属性算择的标准，生成的决策树结构简单，结果可读性好。然而，ID3算法并不适用于连续数据，且倾向于选择多值属性分裂。文献[2?4]提出基于模糊集和粗糙集的改进方案，用条件属性的粗糙度代替属性的信息熵作为分裂的标准，以解决ID3算法倾向选择多值属性的问题。而对于ID3无法处理连续值的问题，文献[5?6]提出C4.5和CART（Classification and Regression Tree）算法。C4.5算法對连续属性进行分割并使分割信息熵最小，采用信息增益率作为分裂属性的标准。而CART算法在属性值连续的情况下，使用最小剩余方差来判定回归树的最优划分，生成回归树。但是C4.5和CART算法的输出结果带有连续属性值的具体范围，不易于理解。因此，仍需在优化结果的可读性上做进一步的工作。客观世界中，存在这样一类数据，在采样时是连续的，在决策时，需用具有较好可读性的离散指标代替原连续值。因此，有必要对连续量进行离散化并深入挖掘该连续量反映的评价等级信息，如在某种对学生的评价中，需将其连续成绩转化为“优”“良”“中”“差”的评价指标。对于这些数据，设计一种高效、可读性强的决策方法是非常必要的。文献[7]提出对于决策树中的连续属性值用聚类算法进行离散化的思路，但是对于这种方法的具体实施、预测正确率、应用场合及局限的研究上仍有待进一步分析探讨。本文提出用K?means++算法离散化连续属性值的思想，并且结合粗糙集的研究成果，改进原有的ID3算法，减少传统ID3算法的运算量。本文在具体数据集中应用改进的ID3算法，通过实验仿真得出改进ID3算法的预测正确率，最后对改进算法的应用场合以及局限作出明确探讨。实验结果表明，本文提出的改进ID3算法在不降低预测正确率的情况下，具有更好的可读性，更少的运算量，适用于需离散化为等级指标的连续数据。

信息增益越大，再划分时所需要的信息量就越小。一般情况下，存在数个条件属性，分别计算每一个条件属性的信息增益，选择信息增益最大的一个属性作为分裂节点。假如存在一个多值属性，这个属性往往会被优先选择作为分裂节点。但是取值最多的属性有可能是在实践中没有意义的甚至是不相关的属性。另外，计算各条件属性的信息熵时，要进行大量的对数运算。在数据集较大的情况下，运算量陡增。因此，有必要针对这两个问题作出改进。

2 基于粗糙集的ID3算法原理

对于上述运算量大和偏向选择多值属性的问题，文献[8?9]提出一种基于粗糙集的改进算法。它的核心思想是用条件属性的粗糙度作为选择分裂属性的标准，无需进行对数运算，减少了运算量，避免了优先选择多值属性。

2.1 决策系统

四元组[S=U，A，V，f]为一个信息系统。其中，[U]为所要验究对象的非空有限集合，为论域；[A]是属性集合；[V=a∈AVa]是属性[a]的值域；[f：U×A→V]是信息函数，其为论域中的每一个对象赋予属性值。若[A=C∪D]，其中，C为条件属性集合，D为决策属性集合，则该信息系统称为决策系统。

2.2 不可区分关系

对于一个决策系统[S=U，A，V，f]，[?B?A]是属性集合的一个子集，称等价关系[IndB]为[S]的不可区分关系，即：

[IndB=x，y∈U×U?a∈B，fx，a=fy，a]

它的含意是仅仅通过属性集[B]无法区分对象[x]和对象[y]，即两者的属性取值相同。

2.3 上近似与下近似

对于一个决策系统[S=U，A，V，f]，[IndB]是等价关系，[X∈U]是一个样例集，它是粗糙的，那么[X]的某些子集可以完全被定义，称为下近似集；可能属于[X]的集合称为上近似集。数学表达式如下：

[BX=xi∈UBxi?X] （5）

[BX=xi∈UBxi∩X≠?] （6）

式中：[BX]为[X]的下近似集；[BX]为[X]的上近似集；[Bxi]为等价关系[IndB]下包含[xi]的等价类。

2.4 属性重要性

设[P，Q∈R]，其中[R]是论域中等价关系的集合。那么[γPQ]表示[P]的分类能力：

[γPQ=cardPXcardX] （7）

式中：card是求模运算；[X]是属于等价关系[Q]下的等价类非空集合。对于[P]下的属性[a]，分别计算[a]加入[P]与未加入[P]时的[γPQ]，可以得出属性[a]的重要性。表达式如下：

[SGAa，P，Q=γPQ-γP-{a}Q] （8）

3 K?means算法及改进

K?means是一种聚类算法，流程如下：在数据集中随机选择k个不同的值作为聚类中心。计算数据集中每一个样本与k个分类中心的距离，并将其归入最临近的一个中心所在的一类。得到一个聚类结果后，再次计算各分类结果的中心，计算样本与中心之间的距离，反复迭代，以至得到一个聚类误差收敛的结果或根据实际情况设定迭代次数。

K?means聚类的结果以及迭代次数与初始值选择有很大关系。为了提高效率、改善聚类结果，必须优化初始值的选择。文献[10]提出K?Means++算法，它的思想是在选择初始值时尽可能地使各初始值的距离最大，可减少迭代的次数，提高聚类效率。

4 改进的ID3算法原理

改进算法的主要思想是首先将数据集中连续的属性取值应用K?means++算法进行离散化，然后计算各条件属性的重要性[SGAa，P，Q]，选择重要性大的属性作为分裂节点。反复迭代，直至所有条件属性均被用作分裂节点。最后剪枝生成决策树。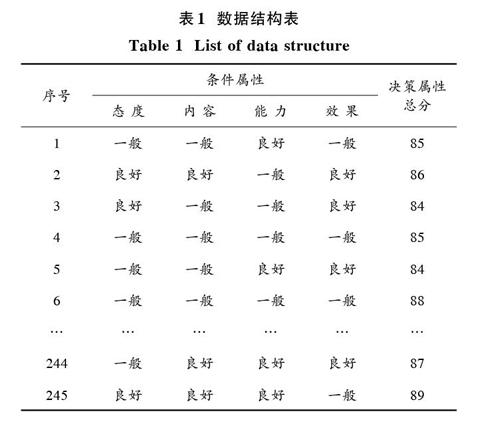

改进的ID3算法主要步骤如下：

1） 数据初始化。

2） 判断属性值是否离散。若离散，则执行步骤3）。否则，确定离散化后取值的个数，应用K?means++算法离散化，并用离散值代替原连续值。

3） 計算活跃的条件属性的重要性，即根据式（8）计算[SGAa，P，Q]的值。

4） 分割样本集，选择重要性最大的条件属性作为分裂节点。

5） 继续分割样本集，重复步骤3）和步骤4）选择剩余的条件属性分割样本集，直至所有条件属性均被用作分裂结点。

6） 剪枝，生成决策树。

5 实验以及结果分析

本文通过分析督导专家对授课教师的听课评价记录，应用改进的ID3算法生成评判授课教师教学水平高低的决策规则。目前本文提出的算法已应用于西安邮电大学的本科教学评估实践中。

5.1 实验数据

本文的数据为近年西安邮电大学督导专家对本校教师的听课评价记录，该数据可在西安邮电大学官网下载。数据集的结构如表1所示，样本的数量为325个。样本中包含4个条件属性和1个决策属性。决策属性是连续的；而条件属性即教师的教学态度、教学内容、教学能力和教学效果，是离散的。所有条件属性下的取值均为“一般”和“良好”两个评价等级。改进算法对连续的决策属性值进行离散化。在离散化过程中，需根据评价体系的不同，确定相应的聚类中心个数。一般而言，二值评价和三值评价体系较为常见。本文采用二值评价体系，将待评教师分为“良好”和“一般”两类。

5.2 实验过程

将样本分为4等份，前3份用作训练数据，最后1份用作测试集。所有仿真均在Matlab 2012软件中完成。本文在二值评价体系中应用改进算法，生成的决策树如图1所示。本文也应用了CART算法分析数据集，作为参照对象。最后分别测试生成的决策树的准确性。测试结果及决策树复杂度如表2所示，其中CART算法的准确率是指在预测值的区间[-0.5，0.5]之内的实际值与所有实际值的比例。

5.3 实验结果分析

二值评价体系下改进算法生成的决策树更为简洁。改进算法的叶子节点已经是教师的评价结果，可读性更好。这是因为CART算法在用条件属性分割样本集后，仅仅对样本作回归分析，并未对样本所反映的评价等级信息进行深入挖掘。而改进算法通过对样本集作聚类，充分挖掘了隐藏的评价等级信息，得出的决策树的可读性更好。另外，改进算法只计算条件属性的重要性，而CART算法生成回归树时，需要对样本实施分割并进行回归分析。因此，改进的ID3算法的计算量比CART算法小，运行时间更短。综上所述，改进的ID3算法适用于本文的教学督导评价数据，具有良好的可读性以及较少的计算量。

6 结 语

ID3算法是数据挖掘中的一种重要算法。针对具体的关于评价体系的数据，本文提出的改进ID3算法用K?means离散连续属性值，通过计算属性的重要性选择分裂节点，生成决策树。实验证明具有更好的可读性及较低的计算量。然而，本文只在二值评价体系下应用了改进算法，对于其他评价体系下的应用仍需做进一步研究。另外，本文提出的改进ID3算法在其他类型数据的应用上也有必要做进一步探讨。

参考文献

[1] 李泓波，白劲波，杨高明，等.决策树技术研究综述[J].电脑知识与技术，2015，11（24）：1?4.

LI Hongbo， BAI Jinbo， YANG Gaoming， et al. Review on decision tree technology research [J]. Computer knowledge and technology， 2015， 11（24）： 1?4.

[2] 翟俊海，翟梦尧，李胜杰.基于相容粗糙集技术的连续值属性决策树归纳[J].计算机科学，2012，39（11）：183?186.

ZHAI Junhai， ZHAI Mengyao， LI Shengjie. Induction of decision tree for continuous?valued attributes based on tolerance rough sets technique [J]. Computer science， 2012， 39（11）： 183?186.

[3] 朱付保，霍晓齐，徐显景.基于粗糙集的ID3决策树算法改进[J].郑州轻工业学院学报（自然科学版），2015，30（1）：50?54.

ZHU Fubao， HUO Xiaoqi， XU Xianjing. Improved ID3 decision tree algorithm based on rough set [J]. Journal of Zhengzhou University of Light Industry （natural science）， 2015， 30（1）： 50?54.

[4] 翟俊海，王华超，张素芳.一种基于模糊熵的模糊分类算法[J].计算机工程与应用，2010，46（20）：176?180.

ZHAI Junhai， WANG Huachao， ZHANG Sufang. Fuzzy classification algorithm based on fuzzy entropy [J]. Computer engineering and applications， 2010， 46（20）： 176?180.

[5] 巩固，吕俊怀，黄永青，等.有效改进C5.0算法的方法[J].計算机工程与设计，2009，30（22）：5197?5199.

GONG Gu， L? Junhuai， HUANG Yongqing， et al. Effective method of improving C5.0 algorithm [J]. Computer engineering and design， 2009， 30（22）： 5197?5199.

[6] 张亮，宁芊.CART决策树的两种改进及应用[J].计算机工程与设计，2015，36（5）：1209?1213.

ZHANG Liang， NING Qian. Two improvements on CART decision tree and its application [J]. Computer engineering and design， 2015， 36（5）： 1209?1213.

[7] 王小巍，蒋玉明.决策树ID3 算法的分析与改进[J].计算机工程与设计，2011，32（9）：3069?3072.

WANG Xiaowei， JIANG Yuming. Analysis and improvement of ID3 decision tree algorithm [J]. Computer engineering and design， 2011， 32（9）： 3069?3072.

[8] LIU X W， WANG D H， JIANG L X. A novel method for inducing ID3 decision trees based on variable precision rough set [C]// 2011 the Seventh International Conference on Natural Computation. Shanghai， China： IEEE， 2011： 494?497.

[9] 翟俊海，侯少星，王熙照.粗糙模糊决策树归纳算法[J].南京大学学报（自然科学版），2016，52（2）：306?312.

ZHAI Junhai， HOU Shaoxing， WANG Xizhao. Induction of rough fuzzy decision tree [J]. Journal of Nanjing University （natural sciences）， 2016， 52（2）： 306?312.

[10] 周润物，李智勇，陈少淼，等.面向大数据处理的并行优化抽样聚类K?means算法[J].计算机应用，2016，36（2）：311?315.

ZHOU Runwu， LI Zhiyong， CHEN Shaomiao， et al. Parallel optimization sampling clustering K?means algorithm for big data processing [J]. Journal of computer applications， 2016， 36（2）： 311?315.

[11] 李晓瑜，俞丽颖，雷航，等.一种K?means改进算法的并行化实现与应用[J].电子科技大学学报，2017，46（1）：61?68.

LI Xiaoyu， YU Liying， LEI Hang， et al. The parallel implementation and application of an improved K?means algorithm [J]. Journal of University of Electronic Science and Technology of China， 2017， 46（1）： 61?68.