GEO卫星姿态偏置对点波束覆盖范围影响

董彦磊 汪春霆 孙晨华 肖永伟

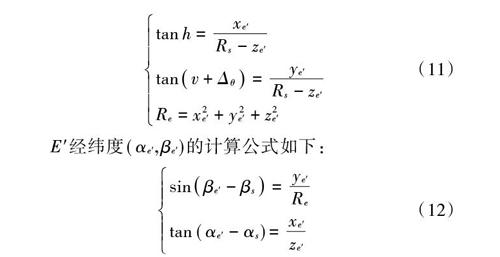
摘 要： 采用多点波束天线技术的GEO卫星在空间运行过程中受地球引力场不均匀、太阳辐射压力变化等因素的影响通常存在滚动姿态、俯仰姿态和偏航姿态的偏差，其点波束的覆盖范围随着偏差角度的变化而变化。滚动偏差造成点波束覆盖范围产生南北方向位移，俯仰偏差造成点波束覆盖范围产生东西方向位移，偏航偏差造成点波束覆盖范围绕星地连线旋转，在南北和东西方向都产生位移。通过理论分析和公式推导，提出卫星滚动偏差、俯仰偏差和偏航偏差对点波束覆盖范围变化影响的计算模型。在实际工程应用中，基于该模型结合点波束偏移量可以逆向推导出卫星的姿态偏差，为卫星姿态控制提供支撑。

关键词： GEO卫星； 滚动姿态偏差； 俯仰姿态偏差； 偏航姿态偏差； 点波束； 覆盖范围

中图分类号： TN927+.2?34 文献标识码： A 文章编号： 1004?373X（2018）15?0001?05

Influence of GEO satellite attitude deviation on spot?beam coverage area

DONG Yanlei， WANG Chunting， SUN Chenhua， XIAO Yongwei

（The 54th Research Institute of CETC， Shijiazhuang 050081， China）

Abstract： The GEO satellites based on multi?point beam antenna technology are usually affected by the factors such as asymmetric earth′s gravitational field and variational solar radiation pressure during the space operation， which may generate the deviations of roll attitude， pitch attitude and yaw attitude， and make the coverage area of the spot?beam change with the angle of deviation. The roll attitude deviation may generate the south?north directional displacement of the spot?beam coverage area. The pitch attitude deviation may generate the east?west directional displacement of the spot?beam coverage area. The yaw attitude deviation makes the spot?beam coverage area rotate around the satellite?to?earth axis， which may generate the omnidirectional displacement. On the basis of theoretical analysis and formula derivation， the calculation model is proposed in this paper， which can reflect the influence of roll attitude deviation， pitch attitude deviation and yaw attitude deviation on the spot?beam coverage area. In the practical engineering applications， the satellite attitude deviation can be derived reversely by the calculation model combined with the spot?beam offset， which provides a support for satellite attitude control.

Keywords： GEO satellite； roll attitude deviation； pitch attitude deviation； yaw attitude deviation； spot?beam； coverage area

0 引 言

采用多点波束天线技术的GEO卫星通信系统具有星上天线增益高、单星覆盖范围大、地面控制系统简单等特点，其应用范围日益广泛。GEO卫星在空间运行过程中，由于受到外力矩的作用会绕其质心产生转动，这种转动使卫星在轨运行期间姿态不断发生变化，产生滚动、俯仰和偏航姿态偏差[1]。由于星地距离远、单点波束覆盖范围一定，卫星姿态的变化将直接导致点波束天线中心指向的改变，进而影响其地面覆盖区域。当卫星姿态发生1°的偏差，地面点波束中心的经纬度偏移可能将达十几度，使点波束完全偏离原覆盖区，直接造成通信中断[2]。

通过构建卫星姿态偏差对波束覆盖影响计算模型，分析卫星滚动姿态偏差、俯仰姿态偏差和偏航姿态偏差对点波束覆盖范围造成的偏移影响，指导实际工程应用中基于点波束中心偏移反推卫星姿态偏差，为卫星姿态控制提供依据，从而最大限度地减少或消除卫星姿态变化对点波束通信造成的影响[3]。

1 构建卫星姿态坐标系

卫星姿态变化通常用滚动角、俯仰角和偏航角偏差来衡量，点波束覆盖范围变化以天线指向地面中心点的变化来标记[4]。通过构建卫星姿态坐标系，定义水平角和垂直角，将卫星滚动角偏差、俯仰角偏差、偏航角偏差与点波束天线指向中心点的变化进行关联，为卫星姿态偏差对点波束覆盖范围的影响分析奠定基础。

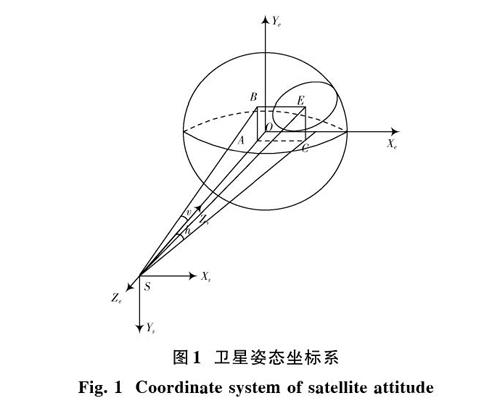
以地心为坐标原点[O]，卫星位置为[S]，地球半径为[Re]，过[S]点的子午面与赤道面的交线为[Ze]轴，以赤道平面为坐标平面，将[Ze]轴向东旋转90°为[Xe]，[Ye]轴与[Ze]轴、[Xe]轴组成右手系指向正北，[Xe]轴、[Ye]轴和[Ze]轴构成地心坐标系。以GEO卫星所在位置为坐标原点[S]，偏航轴[SO]指向地心方向，定义为[Zs]轴，滚动轴以[S]为原点，平行于地心坐标系中[Xe]轴方向定义为[Xs]轴，俯仰轴与[Xs]、[Zs]组成右手系指向正南方向定义为[Ys]轴，[Xs]轴、[Ys]轴和[Zs]轴构成卫星轨道坐标系。将地心坐标系和卫星轨道坐标系统一为卫星姿态坐标系，如图1所示。

在卫星姿态坐标系下定义星下点的位置为[（αs，βs）]，点波束覆盖区天线指向中心点[E]位置为[（αe，βe）]，将点[E]转换为直角坐标系的位置为[（xe，ye，ze）]。

点波束覆盖区天线指向中心点[E]在赤道平面的投影为[C]，在子午面的投影为[B]，[BEC]平面与[Ze]轴的交点为[A]，定义[∠ASC]为天线指向中心点[E]的水平角[h]，[∠ASB]为天线指向中心点[E]的垂直角[v]，用坐标系表示如下：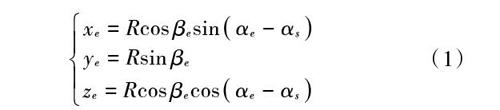

2 点波束覆盖范围计算

在理想情况下，GEO卫星和地球处于相对静止的运动状态，卫星不存在姿态偏差，点波束在地球的覆盖面为球面不规则椭圆形，确定该椭圆的参数包括长半轴、短半轴和中心点[5?7]。

如图2所示，卫星[S]星下点[Z]位置为[（αs，βs）]、卫星到地心距离为[Rs]、地球半径为[Re]、任意点波束覆盖区天线指向中心点[E]的位置为[（αe，βe）]、任意点波束覆盖区椭圆几何中心点为[D]、点波束半功率角为[θ3 dB]、[ABC]为点波束椭圆覆盖面一半，据此计算点波束椭圆形覆盖区域的长半轴长[ai]、短半轴长[bi] 。

根据天线指向中心点[E]和星下点[Z]的位置，利用球面任意两点距离计算公式计算[ZE]：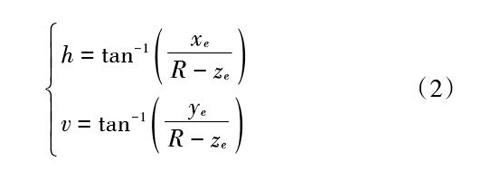

根据三角函数边角关系计算卫星到任意点波束天线指向中心点的距离[Lse]及角[θ]：

根据[θ]和[θ3 dB]，计算[ZA]和[ZC]的球面距离，进而计算得到椭圆长半轴长[ai]。

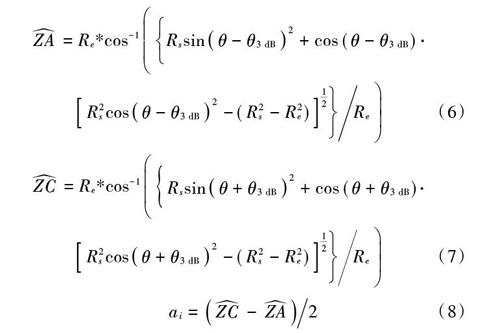
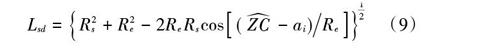
根据[ZC]和[ai]，利用三角函数边角关系计算卫星到点波束覆盖区几何中心点的距离[Lsd]。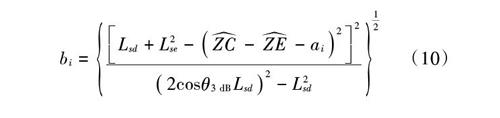

由于[SD]⊥[DB]，[CD]⊥[DB]，計算[DB]长度作为点波束椭圆覆盖区短半轴长[bi]。

3 姿态偏差对点波束覆盖的影响

定义滚动角为卫星绕其自身滚动轴转过的角度，向北为正。当卫星存在滚动姿态偏差时，设偏差角度为[Δθ]，如图3所示，滚动姿态偏差将直接叠加到天线指向的垂直角上，对天线指向的水平角没有影响[8]。

卫星存在滚动姿态偏差时，点波束覆盖区天线指向中心点位置由[E]变为[E]，[E]经纬度定义为[（αe，βe）]，[E]直角坐标系的位置定义为[（xe，ye，ze）]，[（xe，ye，ze）]的计算公式如下：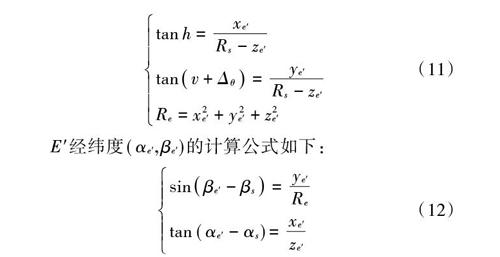

[E]经纬度[（αe，βe）]的计算公式如下：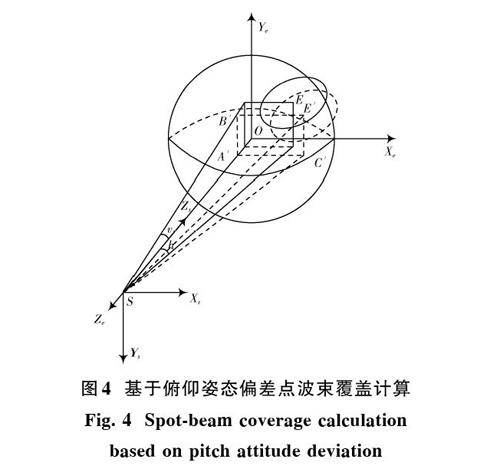

定义俯仰角为卫星绕其自身俯仰轴转过的角度，顺时针为正。当卫星存在俯仰姿态偏差时，设偏差角度为[Δθ]，如图4所示，滚动姿态偏差将直接叠加到天线指向的水平角上，对天线指向的垂直角没有影响[9]。

当卫星存在俯仰姿态偏差时，点波束覆盖区天线指向中心点位置由[E]变为[E]，[E]经纬度定义为[（αe，βe）]，[E]直角坐标系的位置定义为[（xe，ye，ze）]，[（xe，ye，ze）]的计算公式如下：

[E]经纬度[（αe，βe）]计算公式如下：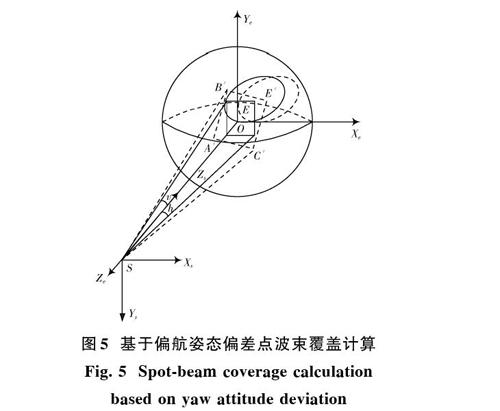

定義偏航角为卫星绕其自身偏航轴转过的角度，顺时针为正。如图5所示，当卫星存在偏航姿态偏差时，设偏差角度为[Δθ]，此时将使波束中心天线指向的水平角和垂直角同时旋转[10][Δθ]。

当卫星存在偏航姿态偏差时，点波束覆盖区天线指向中心点位置由[E]变为[E]，[E]经纬度定义为[（αe，βe）]，[E]直角坐标系的位置定义为[（xe，ye，ze）]，[（xe，ye，ze）]的计算公式如下：

[E]经纬度[（αe，βe）]的计算公式如下：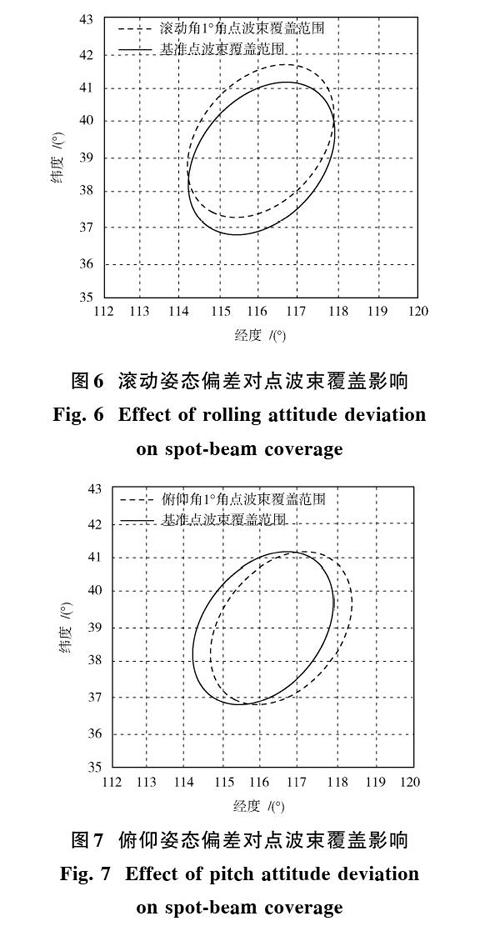

4 仿真实验

当卫星存在姿态偏差情况时，可以利用点波束覆盖计算过程结合卫星姿态偏差角度仿真出卫星不同姿态偏差角度对点波束覆盖范围的影响[11]。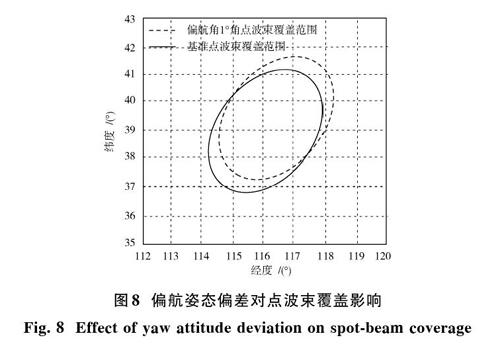

以GEO卫星的位置（100°，0°）、点波束的中心点指向北京（116°，39°）、点波束的半功率角[θ3 dB=1°]为条件，假设卫星滚动角、俯仰角和偏航角均为[1°]，利用点波束覆盖计算过程分别进行点波束覆盖范围变化的仿真。

卫星滚动角为[1°]时，点波束覆盖区域的影响变化如图6所示，通过和基准点波束覆盖区域对比发现，卫星滚动姿态偏差造成点波束覆盖范围在垂直方向进行上下偏移。

卫星俯仰角为[1°]时，点波束覆盖区域的影响变化如图7所示，通过和基准点波束覆盖区域对比发现，卫星俯仰姿态偏差造成点波束覆盖范围在水平方向进行左右偏移。

卫星偏航角为[1°]时，点波束覆盖区域的影响变化如图8所示，通过和基准点波束覆盖区域对比发现，卫星偏航姿态偏差造成点波束覆盖范围在水平方向和垂直方向的都发生偏移，即点波束覆盖区天线中心指向绕星地连线旋转。

5 结 语

通过理论分析和公式推导分别给出了GEO卫星的滚动姿态偏差、俯仰姿态偏差和偏航姿态偏差对点波束覆盖范围影响的计算过程，并给出了相应的仿真结果。通过仿真结果对比发现：当卫星存在滚动姿态偏差时，点波束覆盖范围根据滚动偏差角度在垂直方向进行上下偏移；当卫星存在俯仰姿态偏差时，点波束覆盖范围根据俯仰偏差角度在水平方向进行左右偏移；当卫星存在偏航姿态偏差时，点波束覆盖范围根据偏航偏差角度绕星地连线旋转，在水平方向和垂直方向都发生偏移。

在实际工程应用中通过对点波束中心标校信号的捕获接收和功率测量获取实时的点波束中心指向误差，将其作为输入结合卫星姿态偏差对波束覆盖影响计算模型进行反向推导，可以得出卫星的实际姿态偏差，为卫星姿态控制提供依据[12]，降低了由于卫星姿态偏差导致点波束覆盖范围偏移对地面通信造成的影响。

参考文献

[1] 韩湘，郭新哲，屈会鹏.GEO通信卫星姿态对点波束天线指向影响分析[J].飞行器测控学报，2015，34（1）：77?82.

HAN Xiang， GUO Xinzhe， QU Huipeng. Impact of attitude movement on spot?beam pointing for GEO communication satellites [J]. Journal of spacecraft TT&C; technology， 2015， 34（1）： 77?82.

[2] 汪春霆，张俊祥，潘申富，等.卫星通信系统[M].北京：国防工业出版社，2012：54?261.

WANG Chunting， ZHANG Junxiang， PAN Shenfu， et al. Satellite communication system [M]. Beijing： National Defence Industry Press， 2012： 54?261.

[3] 袁莉芳，杨慧，罗耀辉，等.静止轨道卫星姿态偏置对天线方向图影响的分析[J].航天器工程，2012，21（4）：37?41.

YUAN Lifang， YANG Hui， LUO Yaohui， et al. Analysis on effect of GEO satellite′s attitude offset on antenna pattern [J]. Spacecraft engineering， 2012， 21（4）： 37?41.

[4] 郑炜，李斌，任术波，等. GEO卫星斜投影多波束的椭圆参数分析[J].无线电通信技术，2013，39（1）：5?7.

ZHENG Wei， LI Bin， REN Shubo， et al. Elliptic parameter analysis for inclined projective multi?beam of GEO satellite [J]. Radio communications technology， 2013， 39（1）： 5?7.

[5] 刘龙伟，李文刚，李凤娇.卫星导航定位信息辅助的协作波束赋形算法[J].西安电子科技大学学报，2013，40（3）：7?13.

LIU Longwei， LI Wengang， LI Fengjiao. Cooperative beamfor?ming algorithms using the assistant information from satellite navigation positioning systems [J]. Journal of Xidian University， 2013， 40（3）： 7?13.

[6] 徐慨，鲍凯，何爱林.卫星通信点波束覆盖算法研究[J].舰船电子对抗，2013，36（2）：66?68.

XU Kai， BAO Kai， HE Ailin. Research into satellite communica?tion spot?beam covering algorithm [J]. Shipboard electronic countermeasure， 2013， 36（2）： 66?68.

[7] 《数学手册》编写组.数学手册[M].北京：高等教育出版社，1979.

″Math Manual Writing″ Group. Math manual [M]. Beijing： Higher Education Press， 1979.

[8] 朱玉堂，赵永波，水鹏朗，等.一种低快拍情况下的稳健自适应波束形成算法[J].西安电子科技大学学报，2015，42（6）：37?42.

ZHU Yutang， ZHAO Yongbo， SHUI Penglang， et al. A robust beamforming algorithm in the situation of limited snapshots [J]. Journal of Xidian University， 2015， 42（6）： 37?42.

[9] 李德治，窦朝晖，吕波，等.卫星点波束覆盖区域算法研究[J].载人航天，2009，15（4）：53?55.

LI Dezhi， DOU Chaohui， L? Bo， et al. The algorithm for coverage scope of satellite point beams [J]. Manned spaceflight， 2009， 15（4）： 53?55.

[10] 许国庆，毛新宏，贺中人，等.同步轨道通信卫星天线覆盖图在轨测试方法[J].飞行器测控学报，2013，32（3）：217?223.

XU Guoqing， MAO Xinhong， HE Zhongren， et al. Study on in?orbit test methods for antenna coverage of geostationary communication satellites [J]. Journal of spacecraft TT&C; technology， 2013， 32（3）： 217?223.

[11] 鲍凯，徐慨，项顺祥.基于STK的点波束覆盖分析与仿真[J].通信技术，2013，46（1）：17?19.

BAO Kai， XU Kai， XIANG Shunxiang. The analysis and simulation of spot?beam coverage based on STK [J]. Communications technology， 2013， 46（1）： 17?19.

[12] 陈余军，周志成，曲广吉.小倾角GEO卫星多波束天线覆盖特性优化[J].中国空间科学技术，2014，34（1）：10?17.

CHEN Yujun， ZHOU Zhicheng， QU Guangji. Coverage optimization of inclined GEO satellite with multi?beam antenna [J]. Chinese space science and technology， 2014， 34（1）： 10?17.