滤筒除尘器进风口优化模拟

邓斌程罡樊越胜*王英志胡家雷彭凯文珂

1西安建筑科技大学环境与市政工程学院

2中钢集团天澄环保科技股份有限公司

滤筒除尘器是美国唐纳森公司在袋式除尘器的基础上研发的一种新型除尘器，广泛应用于国内外各个行业，具有除尘效率高（99.9%以上）、阻力小、体型小、维护方便等优点[1-2]。但气流分布不均匀对除尘效率以及滤筒寿命的影响仍困扰着其正常使用。张相亮等人[3-5]用Fluent模拟了袋式除尘器进口对内部流场分布的影响，对设备的优化设计取得了一定的效果，但对于滤筒除尘器出口方式对其流场均匀性方面的研究则甚少。本文将研究滤筒除尘器出口方式对其内部流场均匀性的影响。

1 研究模型

1.1 物理模型

本文研究的除尘器为上、中、下三个箱体组成的下进风滤筒除尘器。如图1所示，其中上箱体尺寸长×宽×高为1200 mm×800 mm×650 mm。中箱体尺寸长×宽×高为1200 mm×800 mm×1150 mm。下箱体为高800 mm的灰斗。进风口为矩形尺寸为150 mm×300 mm，其位于下箱体侧端面距箱体底部450 mm处。出风口为Ф200 mm的圆形管，其位于与进风口端面垂直的侧面距顶部200 mm处。除尘器内花板竖直方向上分布着6个滤筒共两行三列，其中滤筒尺寸长为600 mm，外径为Ф320 mm。

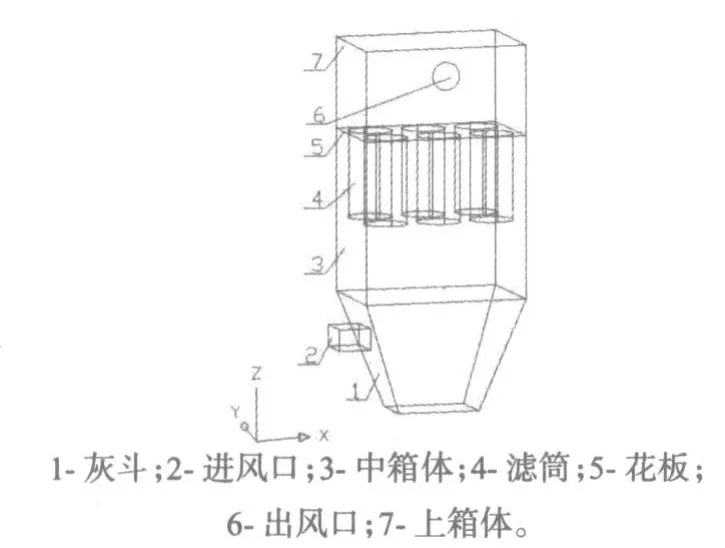
图1 物理模型

1.2 数学模型

1.2.1 流场数学模型

本文为了便于研究，将稀相气固两相流简化为具有平均流体特征的单相气相流；不考虑文丘里等脉冲清灰部件对气流的影响[6]。模拟气相流动时选用κ-ε双方程模型[7-8]。

湍动能κ方程：

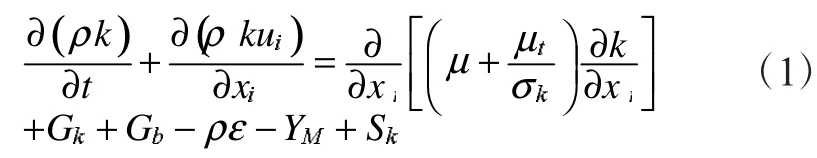
耗散率ε方程：

式中：Gb为由浮力引起的湍动能k的产生项；Gk是由平均速度梯度引起的湍动能k的产生项；YM是由可压缩湍流中脉动扩张的贡献；Sk和Sε是用户定义的源项；C1ε、C2ε、C3ε为常数，C1ε=1.44，C2ε=1.92，C3ε=0.09。σk和 σε是相应的普朗特数，σk=1.0，σε=1.3。

模拟计算时压力-速度耦合采用SIMPLE算法进行求解；对流项选择二阶迎风离散格式[9]。

1.2.2 滤筒数学模型

计算中忽略滤筒褶皱对除尘器内部流场的影响，将滤筒数学模型设置为一维的多孔跳跃介质模型，其具有良好的鲁棒性和收敛性。过滤介质压力变化采用Darcy 定律[10-11]描述：

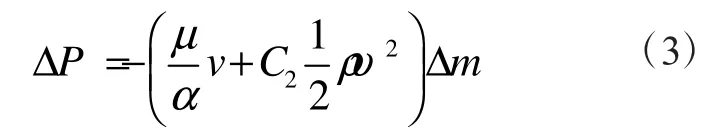
式中：△P为滤筒内外压差，Pa；μ为流体动力粘性系数，Pa·s；α 为渗透率，m2；v 为滤筒外围表面通过的风速，m/s；C2为压力跃升系数；△m为滤筒滤料介质的厚度，m。

1.3 边界条件的设置

为了便于模拟计算，本模型流体选为空气，温度为20℃，密度为 1.205 kg/m3，动力粘度为 1.810×10-5Pa·s。

将进口边界条件设置为速度进口，进口速度υ=13 m/s；出口边界条件设置为压力出口，出口压力P=-1500 Pa；滤料厚度设置为5 mm[12]，渗透率则为α=1.4×10-10m2。

2 流场评价方法

2.1 流量分配系数

滤筒的流量分配系数[13]表示每个滤筒实际处理气体流量与平均处理气体流量的比值，记作Kqi，公式为：

式中：Qi为单个滤筒的实际处理气体量，m3/s；Qmean为单个滤筒的平均处理气体流量，m3/s。

2.2 最大流量不均幅值

最大流量不均幅值是指最大流量分配系数和最小流量分配系数的差值，计作△Kqi。

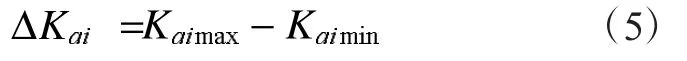
式中：Kqimax为单个滤筒的最大流量分配系数；Kqimin为单个滤筒最小流量分配系数；当气体流量分配不均匀时，Kqi在1.0上下波动；△Kqi≠0时，其值越大表示流场越不均匀，越小则说明流场越均匀；当△Kqi=0，即Kqi=1时，表明流量分配绝对均匀。一般地，当处理风量的相对偏差不大于15%时，便可以认为气体流量分配基本均匀。

2.3 综合流量不均匀幅值

综合流量不均幅值是指所有滤筒的流量分配系数与理想状态下的绝对均匀系数1.0之差的绝对值的平均值。这个参数综合考虑了各个滤筒的流量偏差，评价比较全面，记作，即：

式中：N为模型中滤筒的总个数。

3 模拟方法与结果分析

3.1 模拟方法

本文针对4种不同出口方式进行模拟研究，探索不同出口方式对流场影响规律，以便优化滤筒除尘器结构。如图2～3分别为模型上箱体出口图以及滤筒编号图。

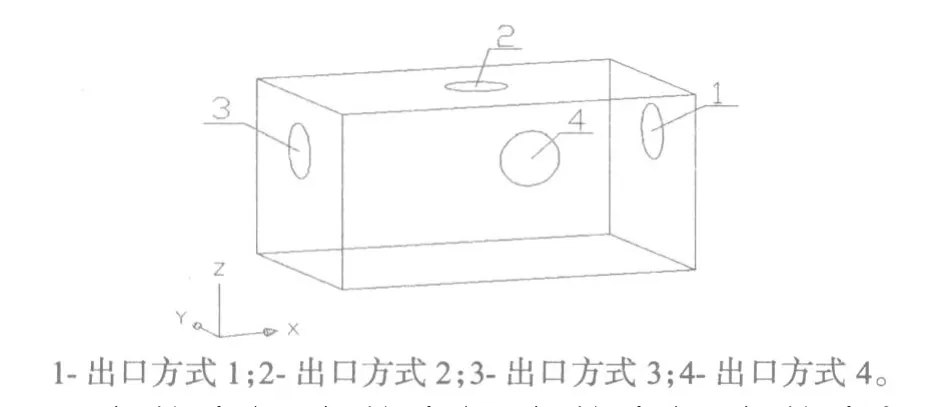
图2 模型出口方式

图3 滤筒编号图

3.2 结果与分析

从图4看出，4种模型的内部流场情况相差不大，气流在进气箱体内沿入口方向形成延伸到后壁面的射流，一部分气流在灰斗斜面的导流作用下，在射流下部形成了下旋涡，容易造成“二次扬尘”，将灰斗中的灰尘重新卷入到射流当中，增加了滤筒过滤负荷。另一部分气流碰到后壁面后向上流动，碰到花板后气体动压转换成高静压，使得气体由后壁面向前壁面横向冲刷，加大了滤筒的冲刷度，一定程度上降低了滤筒的寿命。从图5可以看出靠近后壁面的滤筒冲刷最严重，并依次向前壁面递减，主要是由于气流最先冲刷靠近后壁面的1号和6号滤筒，在1号和6号滤筒的阻挡下减少了1号，2号、3号及4号滤筒的冲刷。

由表1可以看出出口方式3模型的滤筒流量分配情况相对其他3种模型较好，综合流量不均幅值为0.062，最大流量不均幅值为0.169，流量分配并不均匀；流量分配较为不均匀的模型为出口方式1与出口方式4模型，其综合流量不均幅值分别为0.121和0.111；最大流量不均幅值分别为0.288和0.329。其主要原因可能是由于出口3与进风口位于同侧，出口处为静压最低处，而除尘器后壁面处静压较高，这使得气流向靠近前壁面3号和4号滤筒回流的较多。相反当出口位于后壁面时，低静压处与高静压处在同一侧面，使得回流到靠近前壁面3号与4号较少。出口方式4与进口成90°夹角时，根据涡旋理论[14]在此种状况相对于其他三种状况更容易产生涡旋，使内部流场增加了不确定因素，从表1可以看出，靠近出风口一侧的滤筒比另一侧滤筒的流量分配系数要大一些。

图4 模型Y=0.1 m截面速度云图

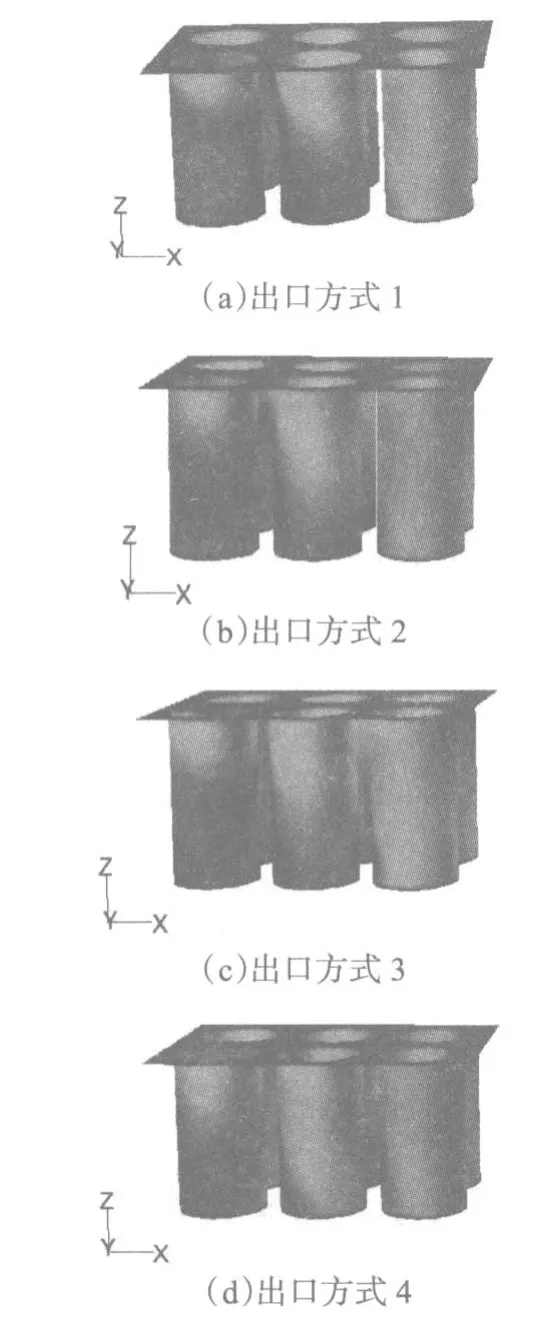
图5 滤筒表面速度云图

由模拟结果可知，出口方式3模型较其他3种模型流场分布情况要好，但4种不同出口模型模拟流场分布都不均匀，其主要原因是由于进风口存在明显的射流，靠近后壁面的滤筒流量分配较大，使得流量分配不均匀的现象比较严重，最终则会导致滤筒寿命的减少。

4 滤筒除尘器结构优化模拟

针对上述模拟存在明显射流及流场分布不均的情况，有必要对进风口进行优化。张相亮、张广鹏等人[3-5]针对下进风袋式除尘器，通过在进风口附近增加导流板和钝体及增加进风口数量较好的改善了袋式除尘器内部流场分布。鉴于在相同过滤风速下，滤筒除尘器较袋式除尘器的通风量要大，进口射流更加明显，为了进一步优化滤筒除尘器内部流场，综合考虑采用等面积的双进风口对滤筒除尘器进口进行优化。其模型如图6所示。

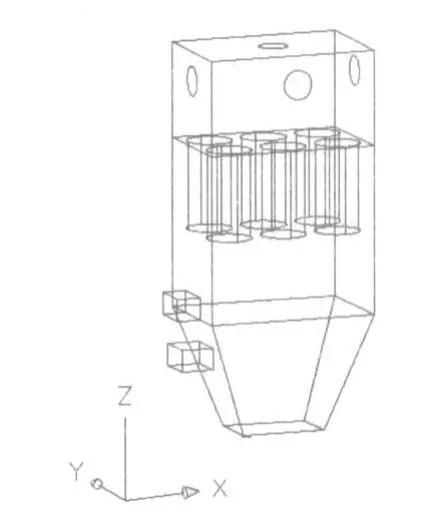
图6 双进风口模型

采用双进风口模型流场分布模拟结果如表2所示，4种出口方式模型的最大流量不均幅值及综合流量不均幅值均有较大程度的减小。其中出口方式4模型最大流量不均幅值为0.228，综合流量不均幅值为0.082，流场分布均匀性较差，但较改进前的最大流量不均幅值降低了31%，综合流量不均幅值降低了26%。其他3种出口方式模型则是比较均匀，出口方式1，方式2和方式3最大流量不均幅值分别较之前降低了63%，58%和33%，综合流量不均幅值分别较之前降低了68%，56%和47%。总体来说，改进后相对改进前的流场分布情况得到了较好的改善。其主要原因是采用等面积双进风口，使进口风速很大程度的减小，很好地改善了射流情况，减少了靠近后壁面的滤筒冲刷程度，使除尘器内部流场分布更加均匀。

5 结论

1）4种出口方式的滤筒除尘器内部都存在明显的射流情况，靠近后壁面的滤筒冲刷较为严重。相比较而言，出口3模型流场分布更均匀，其中出口4模型流场分布情况较差。

2）4种出口方式的模型流场分布不均主要是因为进口风速过大构成的。本文提出双进风口的改进方案，使4种模型的最大流量不均幅值与综合流量不均幅值均有很大程度的降低，很好的改善了除尘器内部流场分布情况。