粉尘浓度对20 L球罐内硫磺粉尘分散过程流场特性的影响*
赵一姝,范健强,白建平,曾 畅,王 雨
(1.重庆科技学院 安全工程学院, 重庆 401331;2.重庆市潼南区经济和信息化委员会,重庆 402660)
0 引言
近年来,国内外粉尘爆炸事故屡屡频发,这些事故涉及的生产行业和粉尘种类十分广泛[1-2],正确评估粉尘爆炸危险性对涉爆企业安全生产和社会安稳具有积极作用。粉尘爆炸特性参数常用来评估粉尘爆炸危险性,但其并不是粉尘固有属性,而与粉尘种类[3]、外界环境及实验设备[4]有密切联系。20 L球形爆炸装置常用于测试粉尘爆炸特性参数,该设备的点火延迟时间被自动设定为60 ms,而实际上点火延迟时间对粉尘爆炸特性参数的测定有很大的影响[5-7],研究表明,粉尘粒径[8]、喷粉压力[9-10]、粉尘种类[11]对最佳点火延迟时间有很大的影响。因此,20 L球形爆炸装置依据单一点火延迟时间测得的有关粉尘粒径和粉尘浓度对爆炸特性影响规律及不同类型粉尘的爆炸特性参数缺乏客观性。
为了解粉尘在20 L球形爆炸装置球罐内的分散规律,学者进行了广泛研究。陈嘉琛等[8-9]利用简化的二维模型研究了铝粉粒径与点火延迟时间段之间的关系;沈世磊等[10]利用简化的二维对称模型研究了粉尘粒径和喷粉压力对球罐内铝粉扩散规律的影响,前者将喷粉压力换算成喷粉速度,后者将喷粉压力定义为常数,实际上在喷粉过程中储粉罐和球罐内的压力梯度逐渐减小,颗粒的初速度并非一成不变,而且二维模型并不能全面反映球罐内流场特性[12];Murillo等[13]和Benedetto等[14-15]利用球罐三维模型研究球罐内湍流动能、流场结构、颗粒分布这些流场参量的演化规律,但并未深入分析流场参量演化的机理,也未确定相应最佳点火延迟时间。为此,笔者建立20 L球形爆炸装置三维模型,借此分析粉尘浓度对球罐内硫磺粉尘的分散过程流场特性的影响规律和各个流场参量之间的内在关联,确定粉尘浓度与最佳点火延迟时间之间的关系。
1 数值模型建立
1.1 几何模型及网格划分
本文建立的三维模型包括球罐、储粉罐、回弹喷嘴和连接管,如图1所示。网格采用非结构四面体网格,回弹喷嘴附近的网格进行加密,共计986 865个网格,最小网格体积为1.2×10-10m3,球罐和储粉罐的壁面、回弹喷嘴及连接管的边界条件都设为wall,相应的DPM边界条件设为reflect。
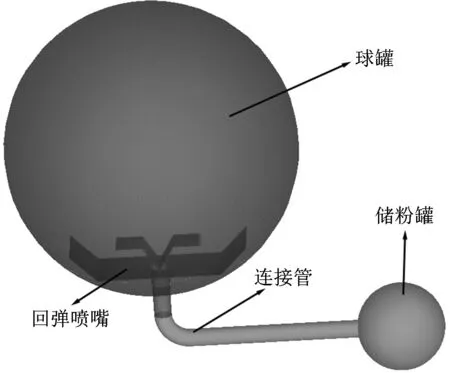
图1 几何模型Fig.1 Geometric model
1.2 模型假设与控制方程
粉尘分散的动力源是储粉罐内压缩空气,因此,假设模型计算域内的空气密度为理想气体,满足理想气体状态方程。采用标准k-ε模型来解释计算域内湍流的变化。通过对非稳态的N-S方程组进行Reynolds分解和平均得到了RANS方程。
连续性方程如下:
(1)
动量守恒方程如下:
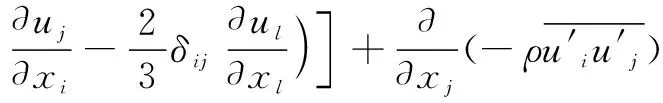
(2)
式中:ui,uj,p和ρ均是平均值和波动值。
假设硫磺粉尘尺寸为圆形颗粒,粒径均匀单一分布,粒径取为163 μm,具体如表1所示。由于3种浓度值的体积分数都远小于10 %,所以选用离散相模型。
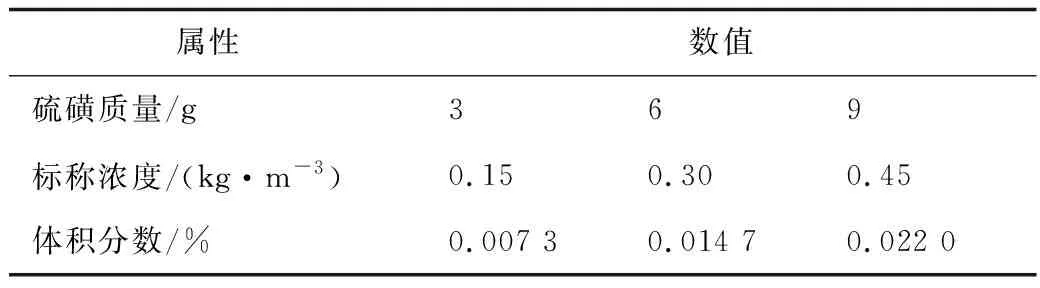
表1 模型的粉尘参数设定Table 1 Dust parameter setting of the model
假设颗粒运动过程中仅受重力、壁面的反射作用及颗粒相与气相之间的曳力作用,忽略其他力的影响。颗粒所受作用力的平衡方程为:
(3)
式中:up为颗粒速度,m/s;ρp为颗粒密度,kg·m-3;u是空气速度,m·s-1;ρ为气体密度,kg/m3;F为颗粒所受重力,N;FD(u-up)是单位质量的颗粒所受到的曳力,N。由式(4)求得:
(4)
式中:dp为颗粒直径,m;μ为流体动力粘度,Pa·s;Re为颗粒的雷诺数,其值可由式(5)得到;式(4)中的CD为曳力系数,其值可由式(6)得到。
(5)
(6)
1.3 参数设置
为客观反映球罐内硫磺粉尘的真实运动情况,依据20 L球形爆炸装置的实验操作流程,将计算域划分为fluid1(高压区域,图1中储粉罐和部分连接管)和fluid2(低压区域,图1中球罐和剩余连接管)。喷粉前,fluid1的初始压力设为2 MPa,fluid1的设为-0.06 MPa。采用SIMPLE算法求解模型压力速度耦合问题,迭代时间步长为1×10-4s,迭代总时间步数为2 000步,每个时间步长最多迭代20次,模拟颗粒在200 ms内的分散过程。
1.4 模型验证
图2储粉罐和球罐内无尘空气扩散过程压力的变化情况,二者压力变化曲线与文献[15]的结果基本吻合。由图2可知,40 ms之后储粉罐和球罐内压力已相对稳定(见图3),波动幅度随时间不断变小。经测量,图1中高压区域的实际体积为0.601 L,低压区域的是20.019 L,根据理想气体方程计算,储粉罐和球罐最终的理论压力为1 411.9 Pa。由图3可知,40 ms之后储粉罐和球罐内计算得到压力与理论值之间的相对误差持续降低。因此,本文建立的20 L球罐内硫磺粉尘分散数值模型是可靠的。
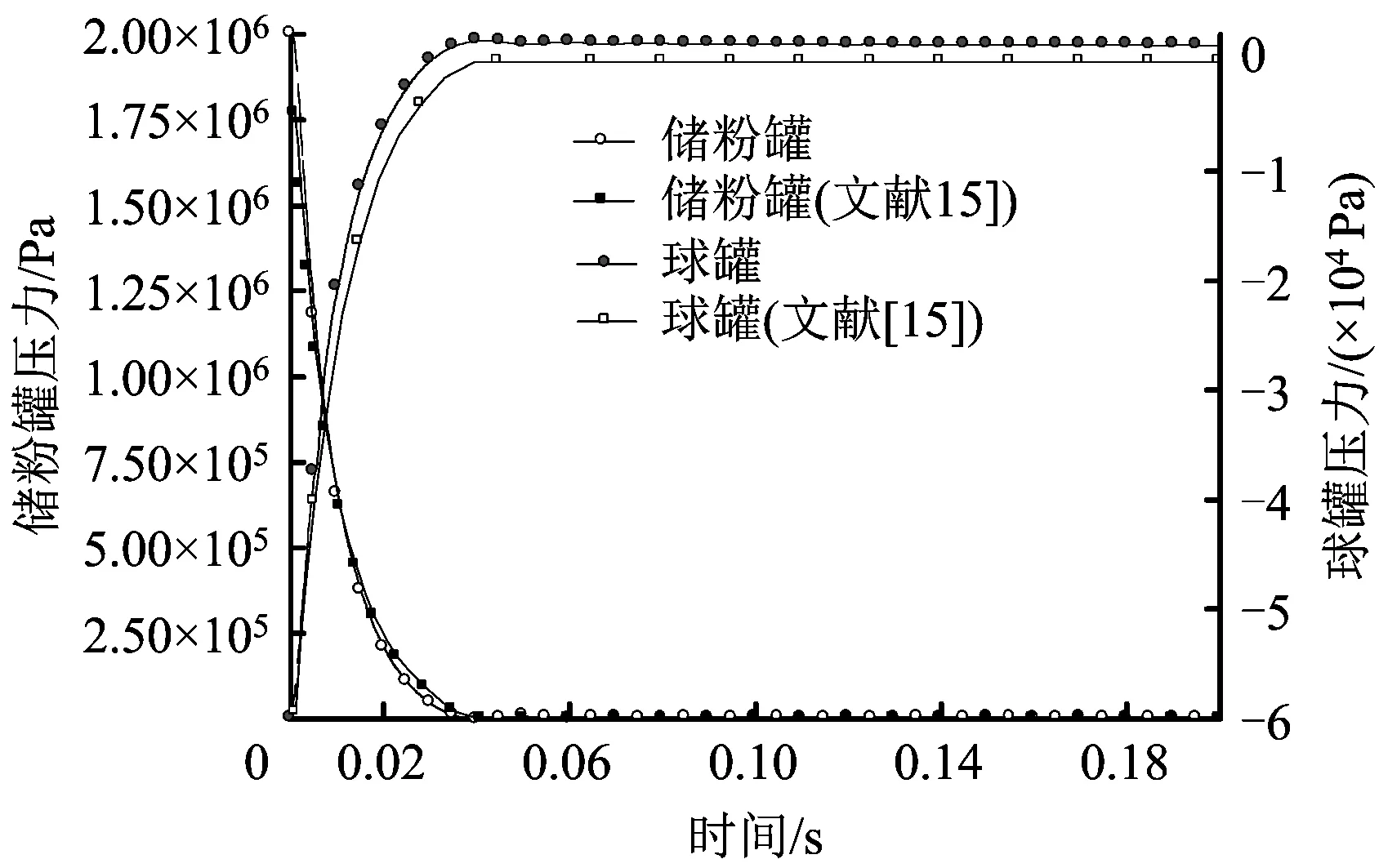
图2 储粉罐和球罐内压力变化规律Fig.2 Variation trend of pressure in the storage tank and the ball tank
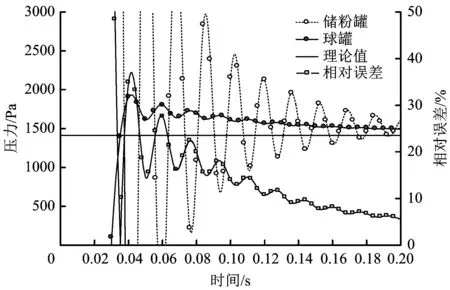
图3 模型计算值与理论值之间的误差分析Fig.3 Error analysis between the calculated value and theoretical value of the model
2 模拟结果及分析
2.1 粉尘浓度对球罐内流场特性参量的影响
图4、图6、图8和图9是粒径为163 μm的硫磺粉尘在3种浓度(0.15,0.3,0.45 kg/m3)的情况下,20 L球罐内流场速度、湍流动能、球心处粉尘云浓度随时间的变化趋势。图5、图7、图10和图11是粒径为163 μm、浓度为0.15 kg/m3的硫磺粉尘在球罐内的流场速度、湍流动能、球心处粉尘浓度、颗粒轨迹在10,60,100,150 ms的变化云图。
由图4可知,球罐内的流场速度先急速上升后又迅速下降,在50 ms已逐渐趋于稳定(见图8)。3种粉尘浓度对应的流场速度在4.2 ms同时增至最大值(88.7,87.9,86.9 m/s),说明喷入的粉尘越少,球罐内流场速度峰值越大。由图5可知,在喷粉阶段,流场存在2个近似对称旋涡,随后2个旋涡顺时针转动,其中1个碰到罐壁和挡板,逐渐消亡,最终2个旋涡合二为一,旋涡中心在球心附近。对于不同的粉尘浓度,球罐内流场速度的变化规律基本一致,同一时刻的数值差异也很小。
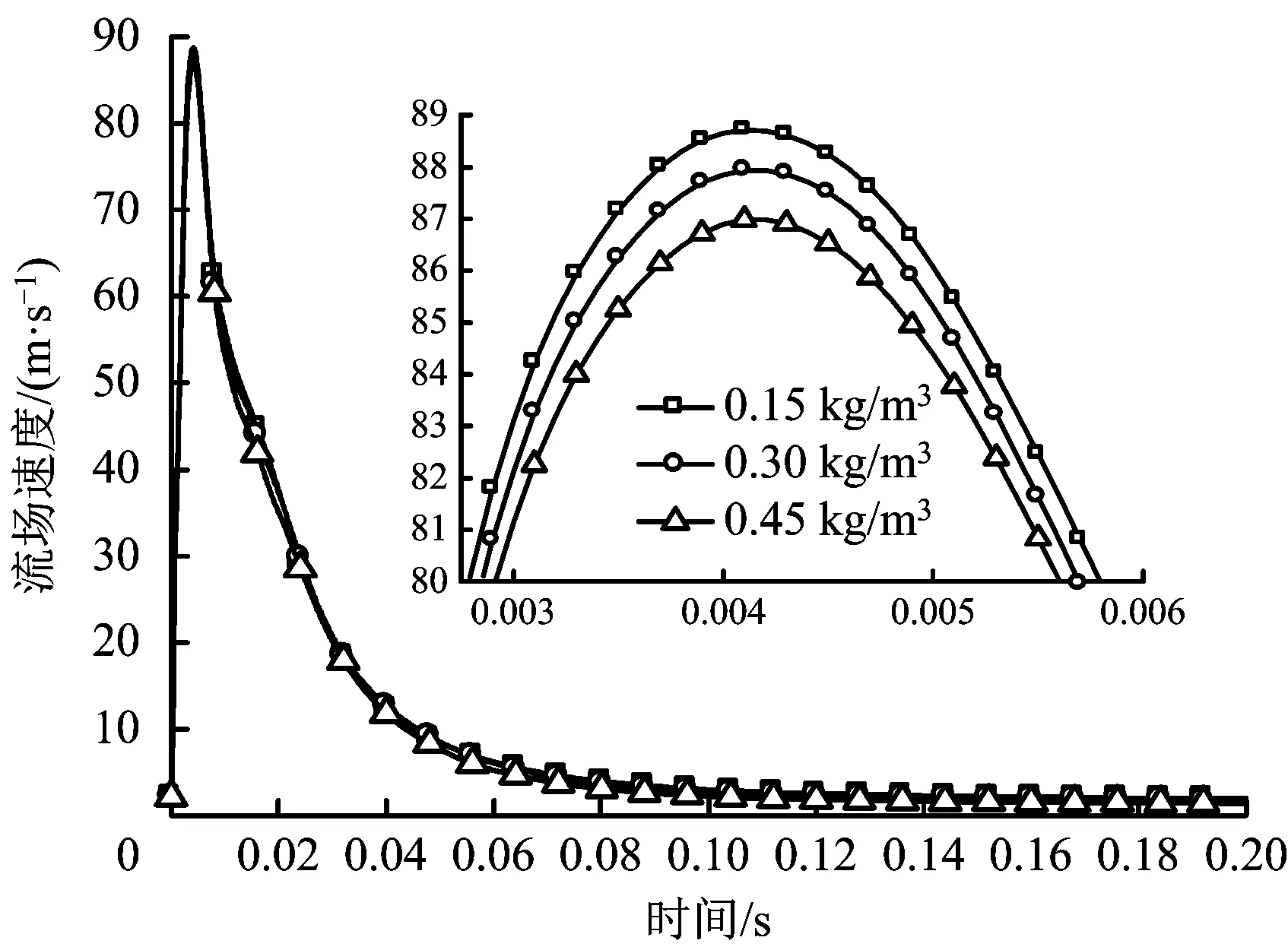
图4 不同粉尘浓度下的球罐内流场速度变化趋势Fig.4 Variation of flow velocity in spherical tank under different dust concentration
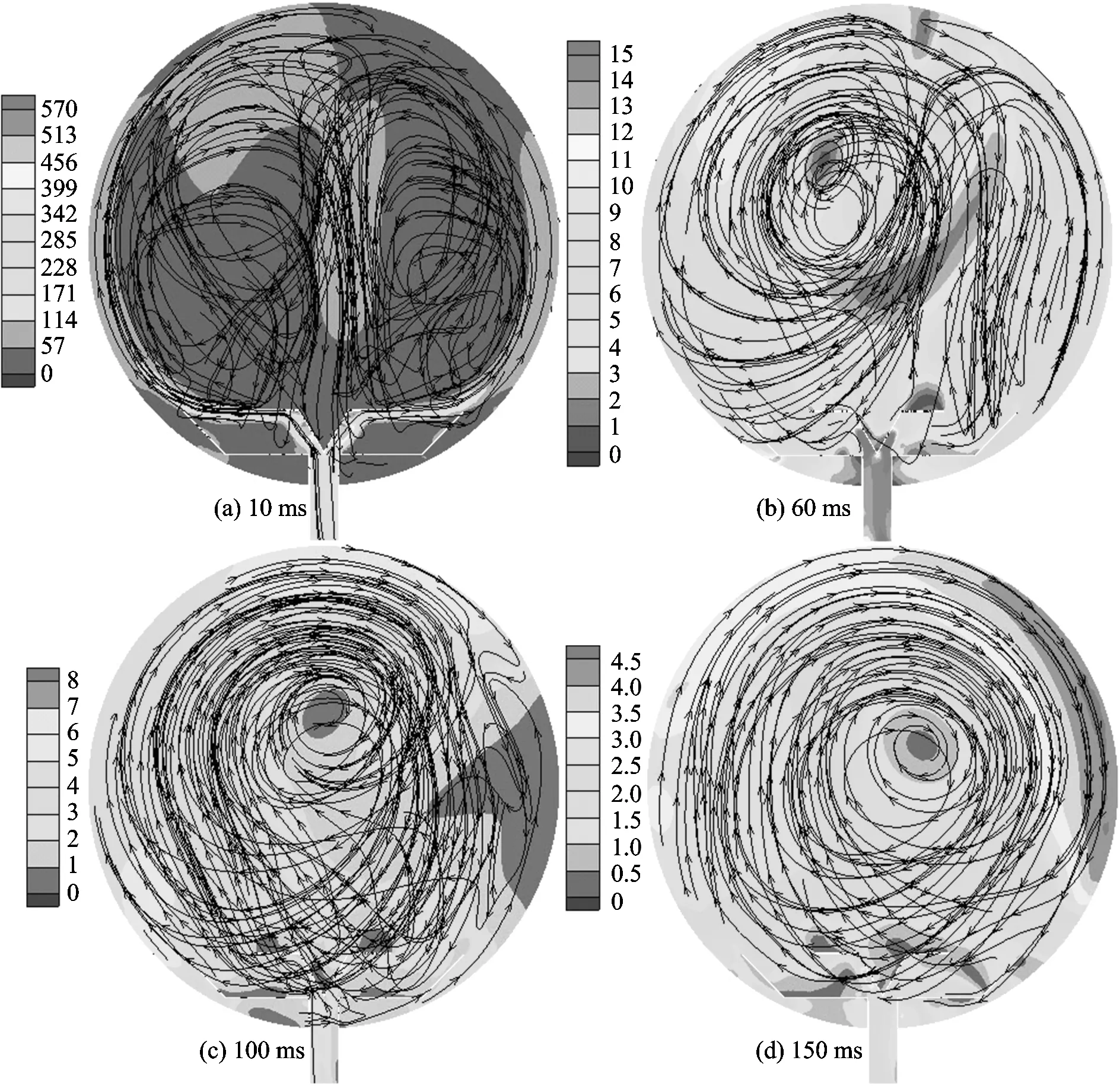
图5 球罐内流场速度的演化历程(单位:m/s)Fig.5 Evolution of flow velocity in spherical tank(unit:m/s)
球罐内的湍流动能先急速上升后又迅速下降(见图6),在50 ms已逐渐趋于稳定(见图8)。3种粉尘浓度对应的湍流动能在6.6 ms同时达到峰值(1 444.5,1 410.2,1 377.0 m2/s2),这说明喷入的粉尘越少,球罐内湍流动能的峰值就越大。由图7可知,在喷粉初始阶段,湍流动能峰值区集中在喷嘴附近,且湍流动能梯度非常大;喷粉结束后,峰值集中在球罐球心附近,距离球心越远,湍流动能越小,湍流动能梯度随时间逐渐降低,在150 ms之后湍流动能梯度已相对较小,各个区域接近一致。对于不同粉尘浓度,球罐内湍流动能的变化规律基本一致,同一时刻的数值差异也很小。
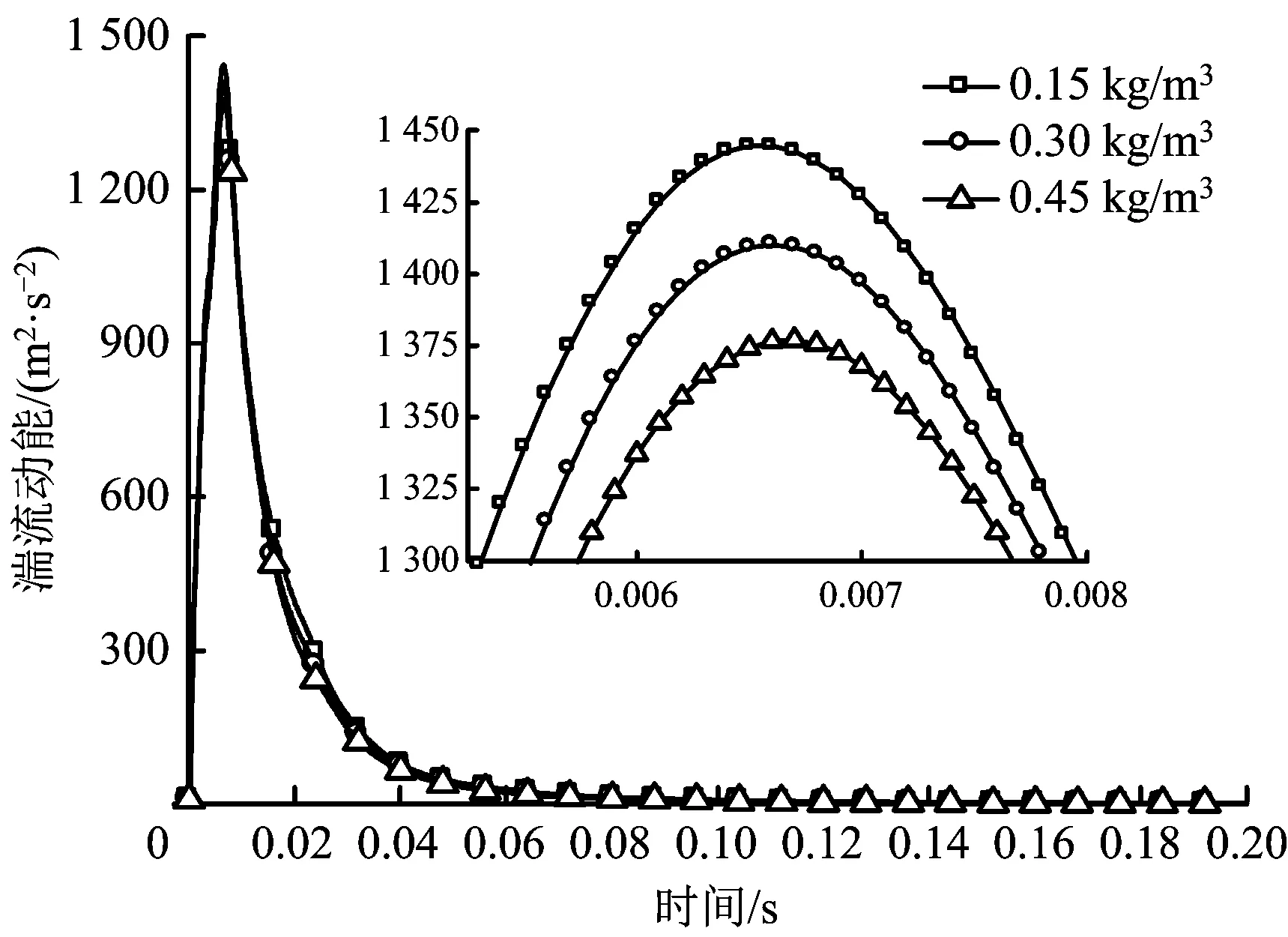
图6 不同粉尘浓度下的球罐内湍流动能变化趋势(单位:m2/s2)Fig.6 Variation of turbulent kinetic energy in spherical tank under different dust concentration(unit:m2/s2)
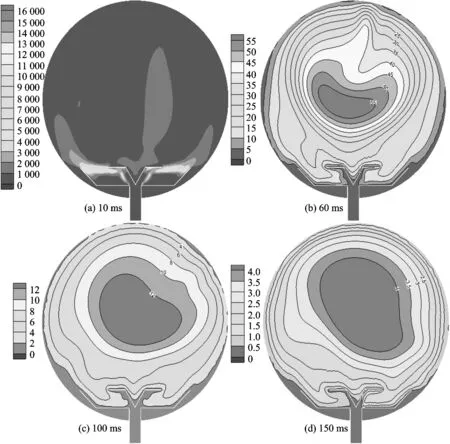
图7 球罐内湍流动能的演化历程Fig.7 Evolution of turbulent kinetic energy in spherical tank
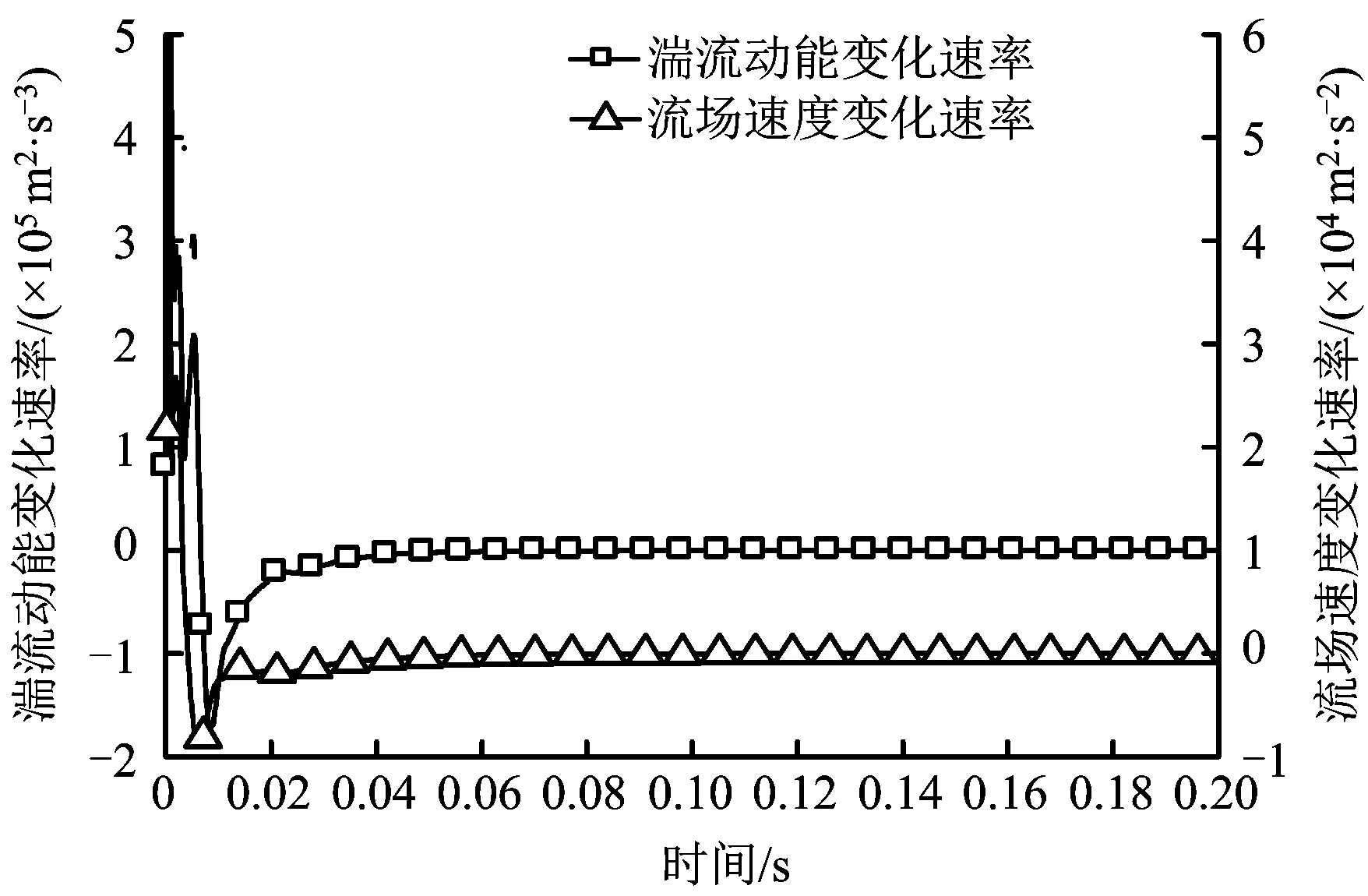
图8 湍流动能和流场速度的3种浓度的平均变化速率Fig.8 Average change rate of three concentrations of turbulent flow and flow velocity
图9为球罐内球心处粉尘云浓度随时间的变化情况,其中“等效浓度”是球心处实际粉尘云浓度与标称浓度的比值(无量纲量)。由图9~11可知,喷粉前期,球罐球心附近的粉尘云浓度较大,在喷粉结束后达到峰值,然后开始下降。3种粉尘浓度对应的粉尘云浓度的峰值分布为1.65,3.71 和6.96 kg/m3,对应的等效浓度分别为11.0,12.4和15.5,这说明喷入粉尘越多,球心处的粉尘颗粒越集中,粉尘云的等效浓度的峰值就大,同时粉尘颗粒滞留在球心附近的时间也越长。
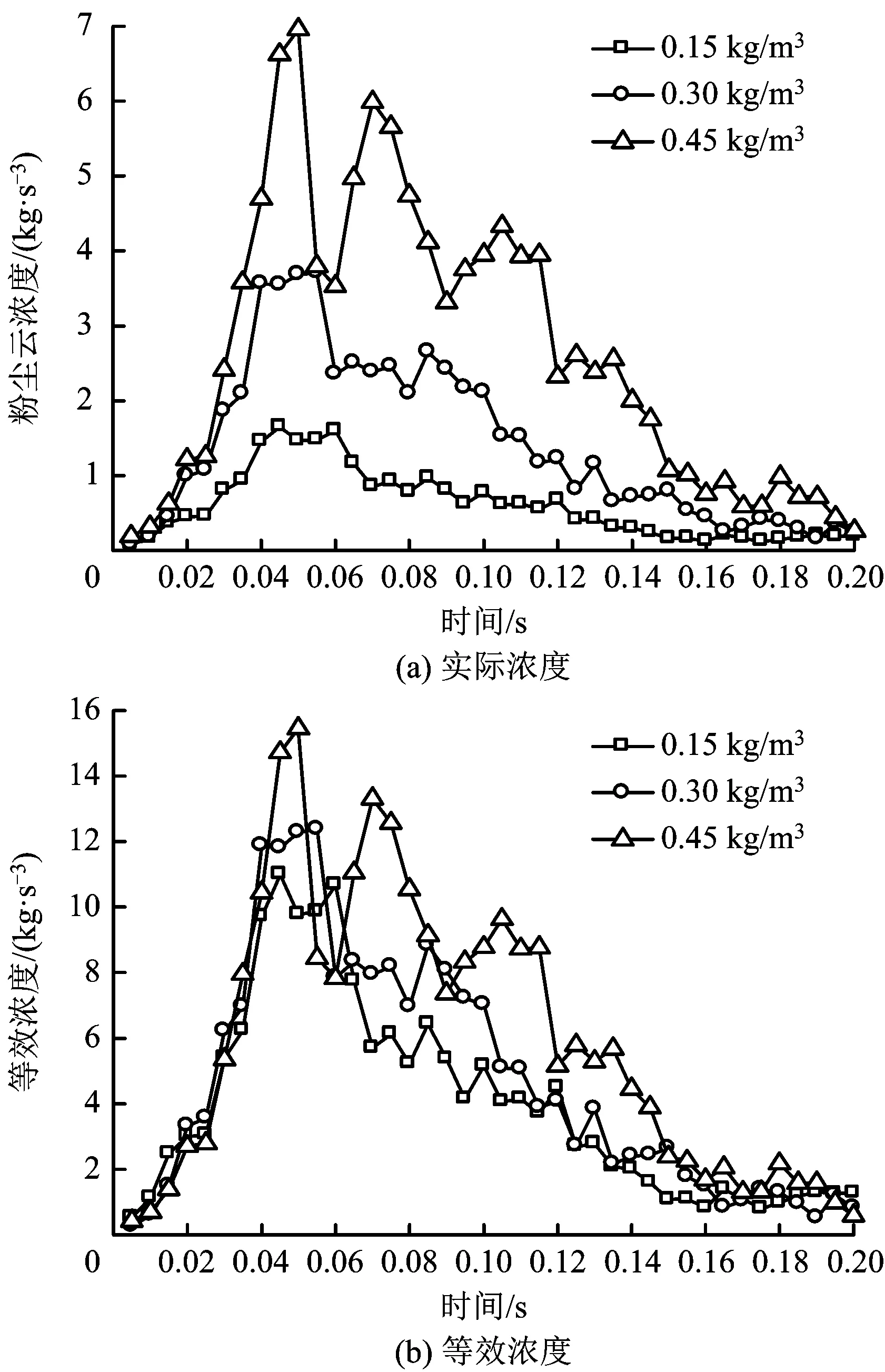
图9 不同浓度下的球罐内球心处粉尘云浓度变化趋势Fig.9 Variation of dust cloud concentration at the center of the spherical tank under different dust concentration

图10 球罐内粉尘云浓度演化历程(单位:kg/m3)Fig.10 Evolution of dust concentration in spherical tank(单位:kg/m3)
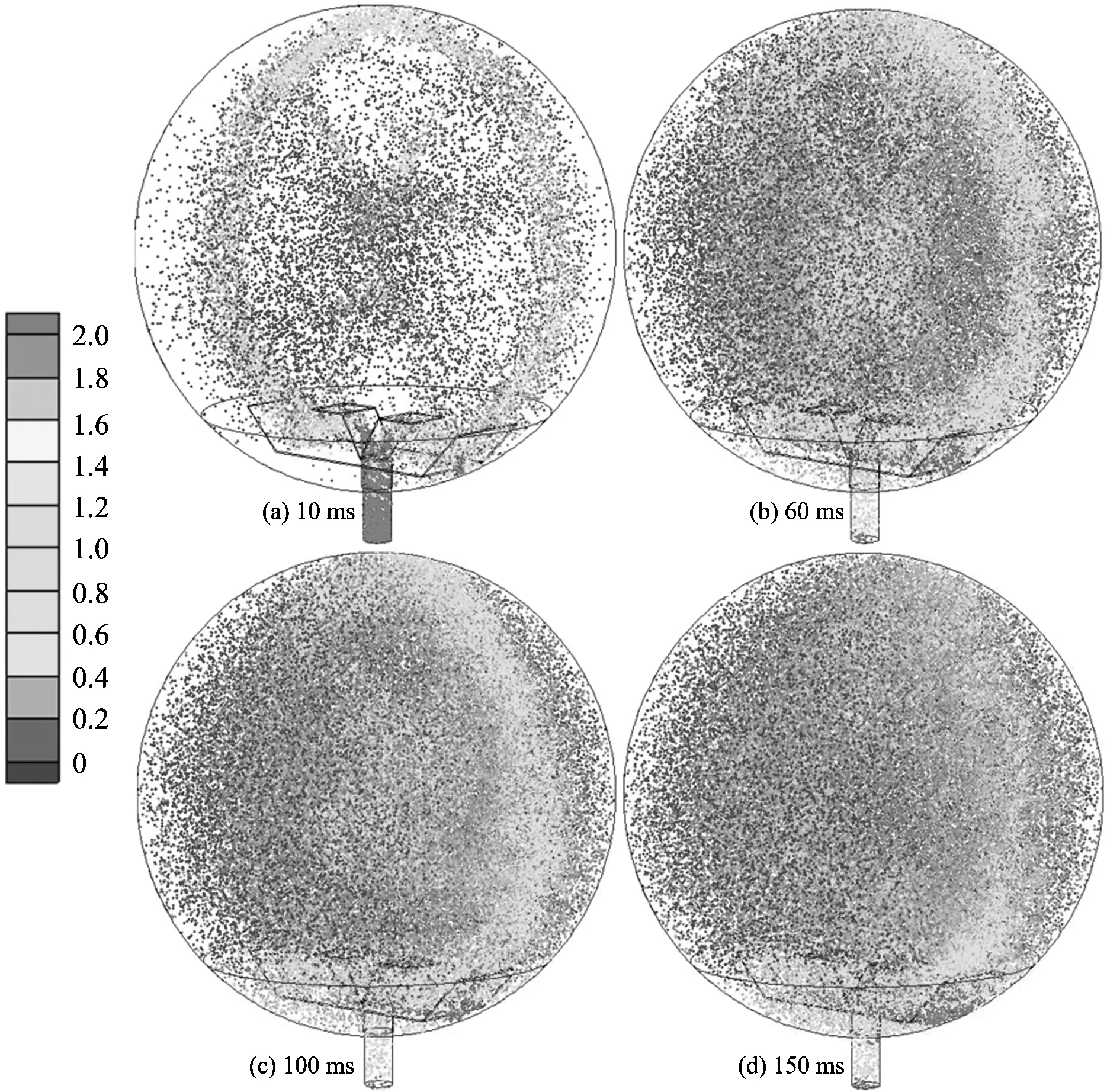
图11 球罐内颗粒轨迹的演化历程(单位:kg/m3)Fig.11 Evolution of particle trajectory in spherical tank(unit:kg/m3)
2.2 球罐内流场特性演化的机理分析
球罐内的颗粒运动期间主要受气流与颗粒之间的曳力和颗粒自身重力的作用,曳力促使气流夹带颗粒绕涡流中心旋转运动,颗粒逐渐向罐壁堆积,重力则使粉尘颗粒向下沉积。喷粉初期,球罐内湍流动能、流场速度、粉尘云浓度和颗粒轨迹云图呈现对称结构(见图5、图7、图10和图11),这是因为喷粉初始阶段喷入球罐的空气和颗粒的初速度很大,颗粒受到的曳力较大,沉降现象不明显。随后储粉罐和球罐之间的压力梯度减小,喷入球罐的空气和颗粒的初速度减小,气流悬浮能力下降,颗粒在重力的作用开始沉降,颗粒群运动开始混乱,流场结构逐渐变为不对称。
粉尘浓度对球罐内的流场特性参数有很大的影响,当其他情况一致时,喷入球罐内的硫磺颗粒越多,球罐内流场速度和湍流动能的峰值越小,球心位置的粉尘颗粒滞留时间越长,而且等效浓度的峰值也越大。这是由于喷粉前期颗粒主要受曳力作用,颗粒的运动由气流控制,当球罐内喷入的粉尘量增多时,球罐内气体“分摊”的能量变少,流场速度和湍流动能变得相对较小。同时,气流对颗粒的夹带作用减弱,颗粒滞留球心处的时间和数量也都增加。
2.3 最佳点火延迟时间的判定
球罐内的残留湍流动能、流场速度和球心处的粉尘云浓度对点火延迟时间均有重要影响。较高的湍流动能和流场速度可以加强点火区域的热量的对流,加速点火区域热量散失,引起淬火效应。同时,在粉尘颗粒尚未大量沉积时点燃粉尘,初始时刻大部分点火能量都能够分散在粉尘颗粒上,点火区域内单位体积内得活化因子将增多,第一时间参与燃烧反应的粉尘也越多,能够提高粉尘的燃烧速率和效率。因此,粒径为163 μm的硫磺的3种浓度对应的最佳点火延迟时间段分别是50~60,50~85和50~105 ms。
3 结论
1)喷粉初期,颗粒受到的曳力较大,沉降现象不明显,因此流场呈现对称结构;随后曳力减小,重力逐渐起主要作用,颗粒开始沉降,颗粒群轨迹发生紊乱,流场逐渐变为不对称。
2)当其他情况一致时,球罐内流场速度和湍流动能的峰值与粉尘浓度成负相关关系,球心处粉尘云等效浓度的峰值和颗粒滞留时间粉尘浓度成正相关关系。
3)当球罐内喷入的粉尘量增多时,球罐内气流速度较小,气流对颗粒的夹带作用减弱,颗粒滞留球心处的时间和数量都增加。
4)粒径为163 μm的硫磺粉尘浓度为0.15,0.3 和0.45 kg/m3对应的最佳点火延迟时间段分别是50~60,50~85和50~105 ms。

