三维测量系统中基于圆锥拟合的旋转台轴线标定新方法

傅屈晨，谢 核，贺峥嵘，彭 真，王国林，李文龙

（1.华中科技大学机械科学与工程学院，湖北 武汉430012；2.中国航发南方工业有限公司，湖南 株洲410000）

航空叶片作为工况恶劣的关键性零部件，表面精度和尺寸精度对其服役性能有着巨大影响，因而对其进行精确测量与质量检测显得尤为关键。传统的三坐标测量法可以一次装夹完成测量，不涉及标定问题。然而其作为接触式测量方法，存在测量速度慢等问题。目前主流的非接触式测量方法有基于相机光学、结构光、激光等，这些方法都具有较高的效率，但是因为一次只能从单个方向测量零件，需要对多视角数据进行拼接。常用的拼接方法有两类：（1）附加标记物，在被测物体上粘贴标记或固定定位球，利用物体几何特征进行匹配[1]；（2）对固定零件的工作台进行标定。由于第一种方法基于测量数据的重合部分进行拼接，零件本身的特征对测量结果影响较大[2]。所以为了准确测量叶片，对旋转台的精确标定是十分必要的。徐永安[1]等人在转台上固定一个标定球，测量已知旋转度数的三个位置的球，通过球心拟合的圆心估算出转轴位置，其利用精度为0.050 mm的测量机得到了0.070 mm的标定精度。解则晓[3]等人则选择将旋转次数设置为六次，进一步提高了标定精度。Meiling Da[2]和胡民政[4]等人利用双球标的方式得到了转台的轴线方向，他们对标定的数学模型进行了简化，假设转台轴线方向与水平面垂直。Jingbo Zhou[5]等人在转台旋转的同时，对固定在其上的材料进行铣削，通过对所得圆柱的测量得到轴线。Bin Sun[6]和Bing Li[6]在航空叶片测量中考虑了探头的倾斜并建立了误差模型。Meiling Da[2]等人则认为相比系统总误差，对旋转台轴线误差进行分析的意义更为重大[2]。

本文考虑转台轴线与水平面不垂直的情况，提出了一种基于圆锥拟合的旋转台轴线高精度标定新方法，将标准陶瓷圆柱固定在转台上，每次转动△θ角，对不同位置的圆柱进行测量，并获得轴线。将轴线拟合成虚拟圆锥，圆锥的轴线即为转台轴线。该方法存在以下两个亮点。第一，传统圆球标定物只存在圆心一个特征点，而本文采用的圆柱标定物能获得更多轴线方向的信息，可有效提高标定数据的准确性；第二，圆锥拟合既标定了旋转台原点位置又标定了其轴线方向，将传统的旋转台标定的3个位置参数改进为6个位姿参数，修正了转台轴线误差，进一步提高了标定精度。

1 旋转台标定数学模型

1.1 坐标系的建立

如图1所示，该三维测量系统运动结构由三轴平移台和旋转台构成。以机器零点OW为原点建立世界坐标系{W}，以大理石平面为xW-yW平面（通过水平仪调节大理石平面与水平面平行）。在转台初始位置建立与转台固接的坐标系{R0}，转台轴线与转台平面的交点OR在世界坐标系W中的坐标为OR（x0R，y0R，z0R），转台轴线单位方向向量为 s（u，v，w）。在转动 θ角度之后坐标系变为{Rθ}。根据从世界坐标系{W}到转台坐标系{Rθ}的齐次变换[9]，三维测点p满足：

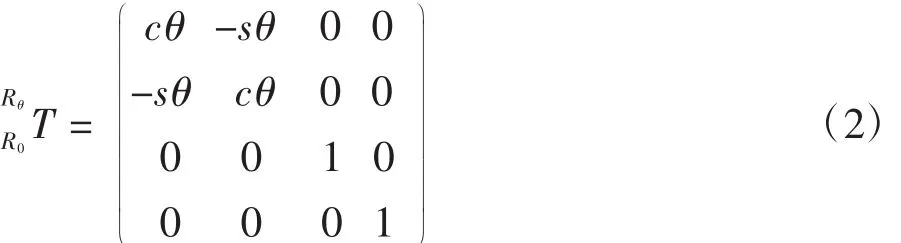
式中 sθ＝ sinθ，c=cosθ，此时只需标定 OR（x0R，y0R，z0R）三个参数。若轴线不垂直于水平面xW-yW，则

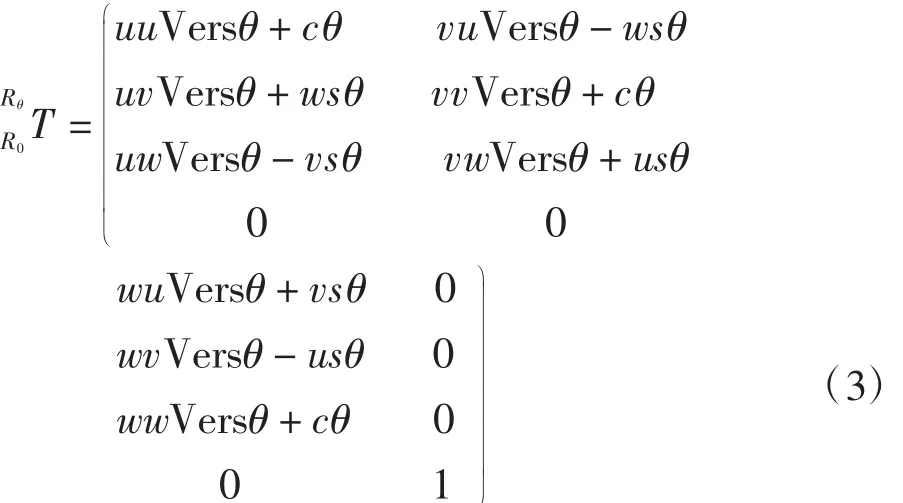
其中Versθ＝1-cosθ，此时还需标定轴线方向s（u，v，w）。因此为准确得到测点，需要转台标定 s（u，v，w）和OR（x0R，y0R，z0R）六个参数。

1.2 基于圆锥拟合的转台标定

首先将标定圆柱固定在转台上，转台每转过△θ度时，在坐标系{W}中测量标定圆柱，通过圆柱拟合得到其轴线，转台转动一周，可得n=360/△θ个位置的圆柱轴线（如图2），为获取转台轴线基点OR和方向s（如图3）的具体数值，需先对所有轴线进行圆锥拟合。设圆锥顶点坐标（xM，yM，zM），母线与轴线 s夹角γ，则圆锥上一点（xi，yi，zi）满足方程：

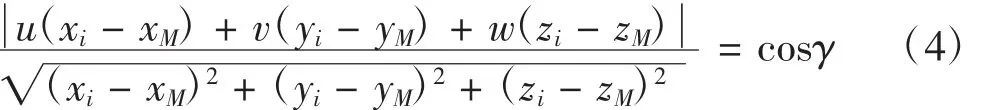
将公式（4）化为二次曲面通式并加入残差项E得误差方程式（5）：

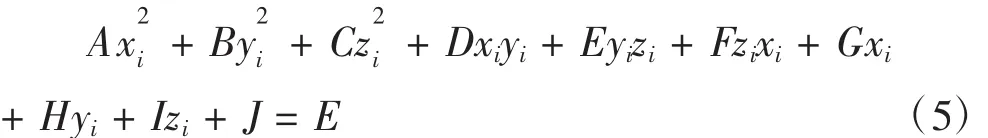
通过对误差E进行最小二乘法可求解二次曲面通式（5）中的参数 A-J：

t=cosγ2；A ＝ μ2-t；B ＝ v2-t

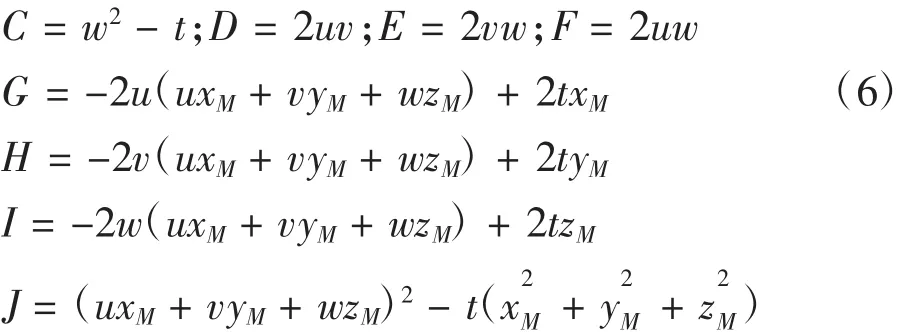
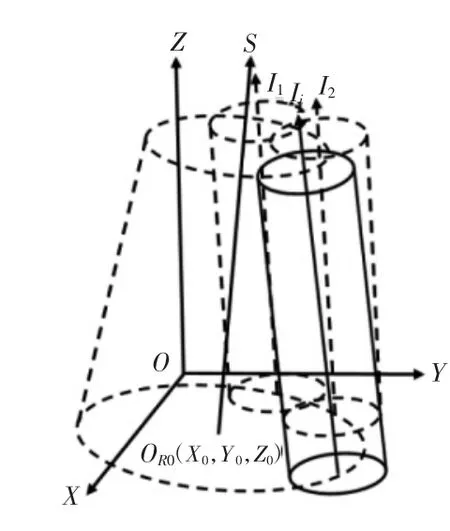
图3 圆锥拟合示意图

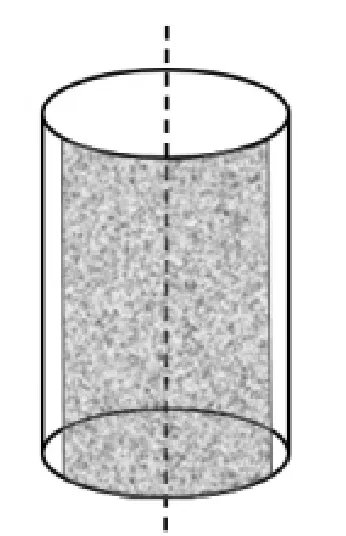
图2 圆柱轴线提取示意图

虽然此方法对多数情况下圆锥拟合效果较好，但在转台标定中因为圆锥半顶角γ过小，且轴线与zw轴近乎平行，方程系数之间巨大差异会导致求解出现病态情况，此方法将不适用。需将二次方程标准化[7]（如图4）。

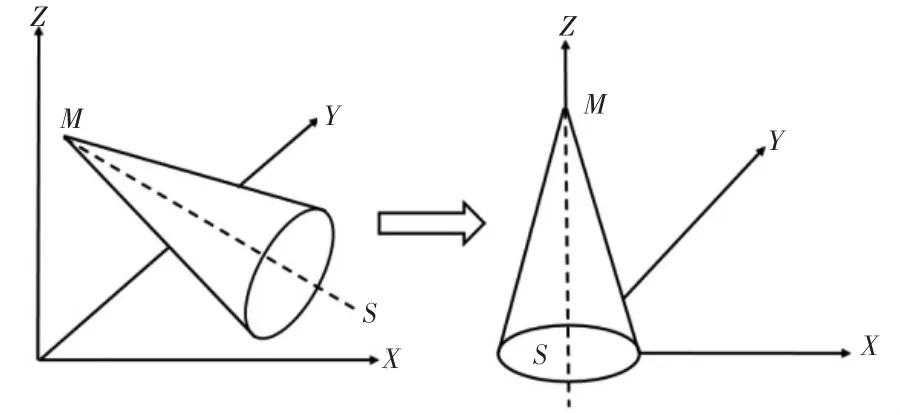
图4 圆锥标准化示意图

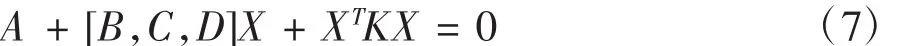
其中，X ＝ [xi，yi，zi]T，由公式（7）构造出转移矩阵K，对其进行奇异值分解：

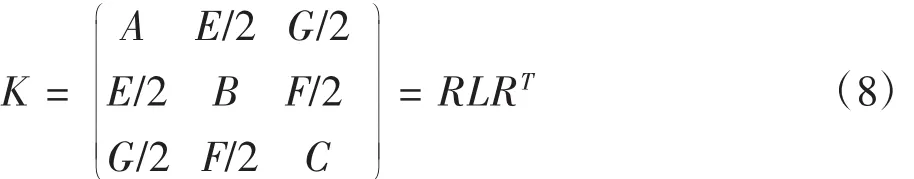
其中 L 表示为可 diag（λ1，λ2，λ3），定义矩阵 R 的第三列为R3，则标定参数表示为：

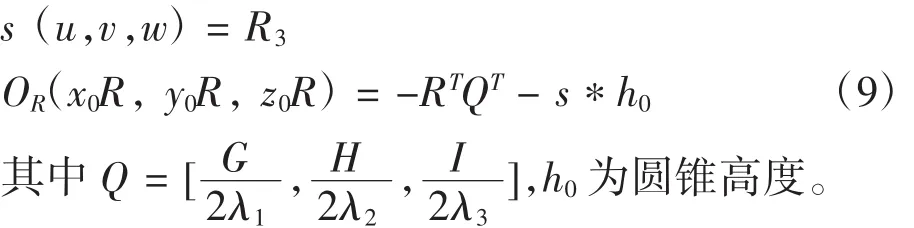
2 仿真测试

2.1 完整圆锥拟合

根据转台直径，拟合出直径为160 mm的部分圆锥面，将曲面离散化生成10万点云数据（如图5）。转台平面zw坐标为-2.663 mm.圆锥拟合得到转台轴线方向误差为0 rad，位置误差为0 mm，均优于圆柱拟合（如图6）。由表1可知当圆锥点云完整时，圆锥拟合与圆柱拟合方法误差均较小。

图5 圆锥点云

图6 圆锥拟合

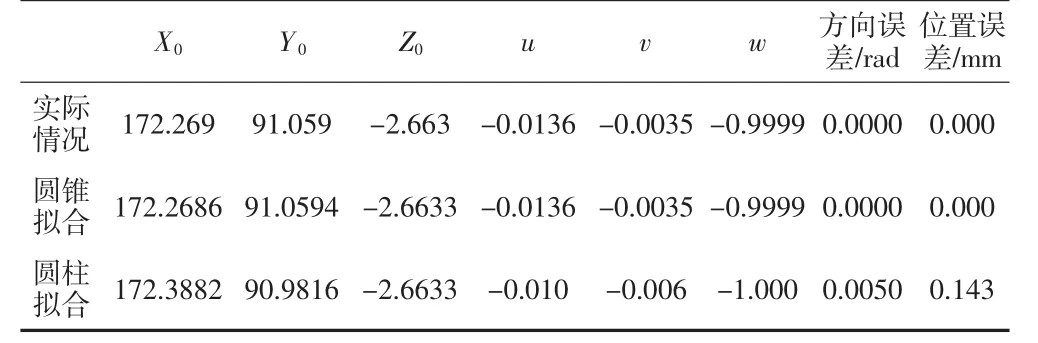
表1 拟合误差分析统计表I

2.2 不完整圆锥拟合

由于实际用来拟合圆锥的是不同位置圆柱的轴线，取八段对称位置的点云模仿实际数据（如图7），但没有引入任何噪音。由表可以看出圆锥出现了较小的位置误差，但由于点云保持对称性，方向误差仍然为0 rad，优于圆柱拟合效果（如图8）。由表2可知当圆锥点云不完整时，圆锥拟合与圆柱拟合方法误差均增大。

图7 不完整点云

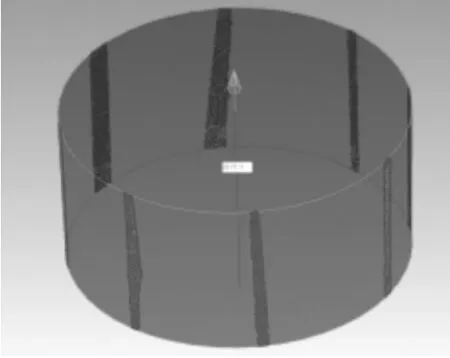
图8 圆锥拟合

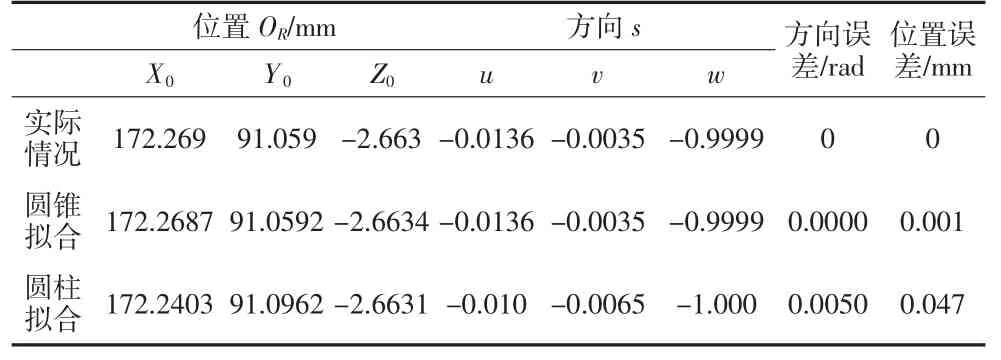
表2 拟合误差分析统计表II

2.3 加入高斯噪音

在拟合实际数据时，噪音是无法避免的，噪音的引入会导致较大的形状误差，从而导致较大的标定误差。为了进一步模拟实际测得数据，分别给完整点云和不完整点云加入标准差为0.001 mm～0.02 mm的高斯噪音，如表3所示。可见随着噪音的增大圆柱拟合圆锥拟合的精度都随之下降，但圆锥拟合误差在位置和方向始终比圆柱拟合低一个数量级以上。

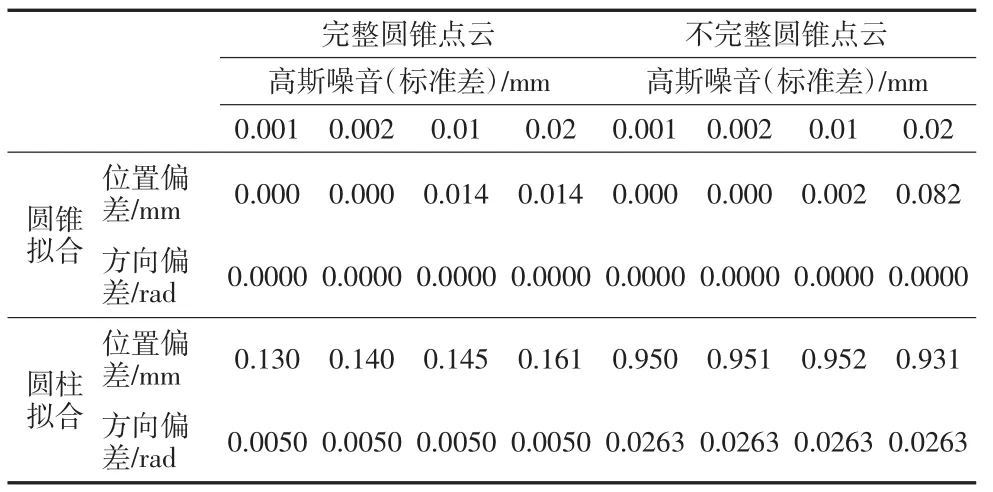
表3 拟合误差分析统计表III

3 实验

3.1 旋转台标定实验

三维测量系统由三维移动平台，转台和点激光测头组成。测头精度为0.010 mm，最大测量角度170°，测量频率1 000 Hz.移动平台x轴重复定位精度为0.012 mm，y轴0.010 mm，z轴0.018 mm.行程由光电限位开关决定（287.00 mm，287.00 mm，437.00 mm）。通过对八个位置圆柱的测量并对其轴线进行圆锥拟合（如图9），标定获得转台轴线方向为 s（0.000 1，-0.001 1，1），基点为 O（R126.453 9 mm，254.054 6 mm，0 mm）（如图 10）。圆柱拟合所得参数为 s（0，0，1），OR（126.583 5 mm，254.019 8 mm，0 mm）。

图9 陶瓷圆柱测量

图10 轴线标定

3.2 测量实验

为了评估测量效果，本文采用华中科技大学数字制造装备与技术国家重点实验室自主开发的i－Cloud3D三维检测软件，该软件具备点云精简、光顺、匹配与误差三维误差分析等功能。

如图11为待测圆柱面的模型点云图。对圆柱面进行测量时，转台的单次旋转角为45°，将叶片点云通过标定参数进行拼接，标准偏差为0.032 mm（如图12）。圆柱的拟合标准偏差为0.042 mm（如图13），局部放大后可见待拟合的圆柱点云出现明显分层现象（如图 14）。

图11 圆柱点云

图12 圆锥拟合标定

图13 圆柱拟合标定

图14 点云分层

对两种型号的叶片模型进行测量。叶片1长宽高为（1 190 mm×580 mm×1 940 mm），点云数量为298 179（如图15）；叶片2长宽高为（1 064 mm × 630 mm × 1 900 mm），点云数量为 228 533（如图 16）。为减小测量误差，实际测量时要尽量将被测物体置于转台中心，从而旋转产生的偏差会减小[1]（如图17）。

图15 叶片1点云

图16 叶片2点云

图17 叶片测量

转台的单次旋转角取180°.将叶片点云通过标定参数拼接，可得叶片模型标准偏差分别为0.082 mm（如图 18）和 0.087 mm（如图 19）。经实验验证，圆柱拟合的标定误差明显大于圆锥拟合。同时因为圆锥锥度过小，顶点往往离底面基点距离极远，需要迭代算法来确定最佳拟合。

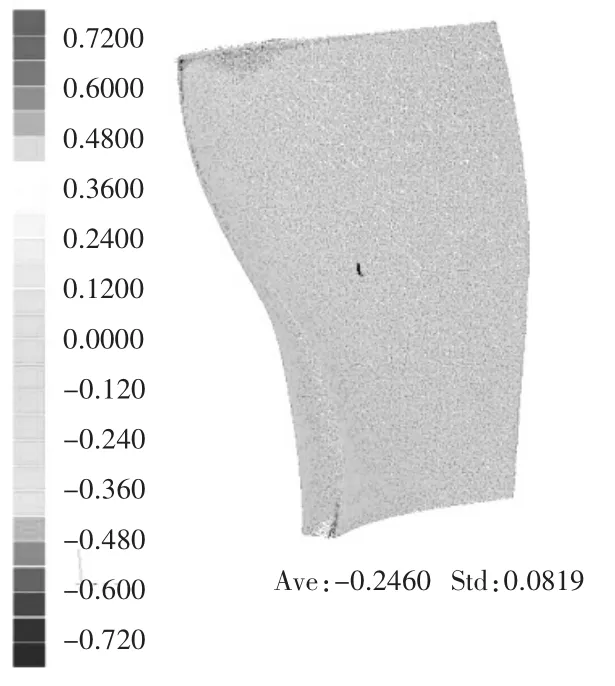
图18 叶片1拟合误差图

图19 叶片2拟合误差图

4 结束语

本文考虑旋转台轴线方向不与水平面垂直的情况，提出了一种基于圆锥拟合的转台标定新方法。使用标准陶瓷圆柱对转台轴线进行了精确标定。利用三轴重复定位精度为0.024 mm的三维点坐标测量系统获得了转台轴线基点位置标准偏差为0.032 mm的标定结果。标定与测量实验表明，与圆柱拟合相比，该标定方法精度更高。