LBM三维相场模型模拟并行方法研究
贾金芳 薛万东 邓新 曹腾飞 冯力 杨培
LBM三维相场模型模拟并行方法研究
贾金芳*薛万东 邓新 曹腾飞 冯力 杨培
青海大学计算机技术与应用系,青海 西宁 810016
以高纯丁二腈为研究对象,基于MPI并行求解了耦合流动场的三维枝晶非等温生长PF-LBM相场模型,解决其存在的计算量巨大、计算时间长、模拟规模小的问题。模拟结果表明,MPI并行求解技术不仅可以在一定程度上扩大可模拟规模,而且也可以在同条件下获得较高的加速比。相同的流动对三维枝晶生长过程的影响机制同时也说明了采用MPI并行算法的正确性和有效性。
相场模型;三维;LBM;MPI
凝固过程中材料微观组织形成与生长演化对材料使用性能有重要影响[1]。枝晶凝固过程受多种参数和复杂边界条件的影响,实际试验成本比较高[2]。使用计算机进行微观组织数值模拟因其低成本、便捷等优势备受关注。相场法作为一种数值计算技术,应用于凝固过程的模拟,可直观再现复杂的微观组织演化过程,自问世以来就受到各国研究者的关注[3-4]。
凝固微观组织数值模拟中,流场数值模拟的难度较大。而格子玻尔兹曼方法LBM(Lattice Boltzmann Method)被认为是模拟流场时最有前途的求解方法。相对于传统流场计算方法,LBM方法具有天然并行性、算法较简单、易于处理复杂边界条件、求解更容易等优点[5],一直以来受到很多领域学者的关注,并得到了广泛的应用。
因此,本文将LBM方法与KARMA等[6]提出的纯物质相场模型结合,忽略重力和动力学影响,建立了耦合流动场的三维枝晶非等温生长PF-LBM(Phase-LBM field model)模型,研究对流作用下枝晶生长机理。然而,计算量大一直是制约相场法推广和应用的一个劣势,相场法耦合流场后,在原有的尺度上增加了新的空间和时间尺度,三维也比二维增加了一个维度,其计算量更大,加之计算机本身硬件条件的限制,其模拟规模都比较小,仍缺乏定量研究。另外,目前相场模型一般采用有限差分方法求解[7-9],其在整个求解域对控制方程进行同尺寸均匀离散,导致计算量巨大,限制了三维凝固微观组织模拟的发展。所以,为了更切实际地反映金属凝固的微观组织演化过程,对微观组织演化在多尺度进行多场耦合三维定量模拟具有重要意义,研究更快速、合理的数值求解方法来求解多场耦合三维相场模型显得很有必要。
表1 SCN热物性参数、相场参数及计算参数

随着多核CPU及GPU大规模并行机的出现,学者们逐步致力于研究并行算法,以解决计算成本,实现高效定量模拟。George等[10]使用MPI并行技术成功实现了较大区域内使用有限差分方法的三维合金枝晶微观组织凝固模拟。Altenfeld等[11]应用OpenMP侧重于并行迭代线性方程的求解和非线性的相场方程显式求解器的并行使用,这两个求解器用于基于相场法的微观组织演变模拟。在GPU方面,Aoki等[12]在多GPU集群上对三维枝晶生长过程进行了模拟研究,结果在很大程度上提高了计算效率,扩大了模拟规模。同时期,Yamanaka、Shimokawabe等[13-14]分别在单GPU和配有多个GPU的TSUBAME 2.0超级计算机上对相场与溶质场两场耦合、三维二元合金凝固相场模型进行了模拟,结果证明GPU并行计算可实现快速、高效、大规模定量模拟,其性能是单机或多核CPU无法比拟的。
尽管上述研究都使用了不同的并行数值求解方法求解相场模型,也在一定程度上取得了较好的结果,但是这些研究基本都是对三维两场耦合相场模型的模拟实现。因此,本文将基于消息传递接口MPI实现对三维多场耦合相场模型的并行求解,在一定程度上扩大计算规模,提高计算效率,为材料研究学者实现更真实的微观组织模拟奠定基础。
1 相场模型
1.1 LBM方法
LBM演化方程为
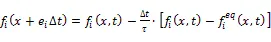
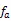

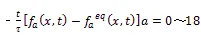
1.2 相场模型
相场和温度场控制方程分别表示为

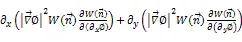

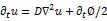
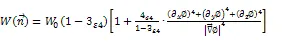
将质量守恒方程和动量守恒方程以下述方式耦合到相场方程中,为统一描述液相区和枝晶间液体金属的流动,假定凝固过程中流动不引起晶粒位置的改变。
质量守恒方程(连续性方程)为
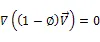
动量守恒方程为


2 模拟参数取值及数值计算
2.1 模拟参数取值
本文选择高纯丁二腈SCN为研究对象,其热物性参数、相场参数及计算参数如表1所示。
2.2 初始、边界条件
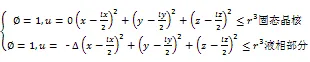
式中:x、y、z分别为三个坐标轴方向;lx、ly、lz为三维模拟区域分别在三个坐标轴方向上的最大网格数。
在计算区域边界处,相场和温度场均采用了Zero-Neumann边界条件。流场边界条件对计算结果的精度和稳定性有很大影响。在LBM流场方面,本文采用的边界条件是启发式格式中的用于固体壁面处理的反弹格式,此格式常用于处理无滑移边界问题。与其他边界条件相比,它不需要较复杂的数学推导和公式求解,其可以根据边界上的一些宏观物理特性如对称性等,通过微观粒子的运动规则直接确定边界节点上的未知分布函数。
2.3 数值求解方法
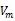
在数值求解方面,由于问题及算法本身非常符合可被并行的特点,本文主要基于MPI中对等模式实现三维多场耦合相场模型并行求解,其中每个节点的负载、地位都是平等的。将三维求解区域按列划分成相同大小的多个子区域,每个节点负责其中一个子区域的计算,同一时间步内所有计算完成后,在开始下一时刻计算前,必须完成每个子区域边界网格点值的更新,即每一节点与相邻节点间须进行数据通信。基于MPI并行求解模式如图1所示。
3 结果与分析
本文实验计算环境为计算机系“三江源数据分析中心”高性能集群服务器平台,其系统配置为:CPU型号Intel Xeon E5-2620 v2 @ 2.10GHz,共48个计算节点。
3.1 模拟结果
图2(a)、(b)、(c)依次为没有耦合流动时枝晶生长形貌、沿x轴方向中间位置相场切片图和与之对应的温度场切片图,可以看出,枝晶各分支均呈现对称生长,温度场边界层厚度也保持一致。
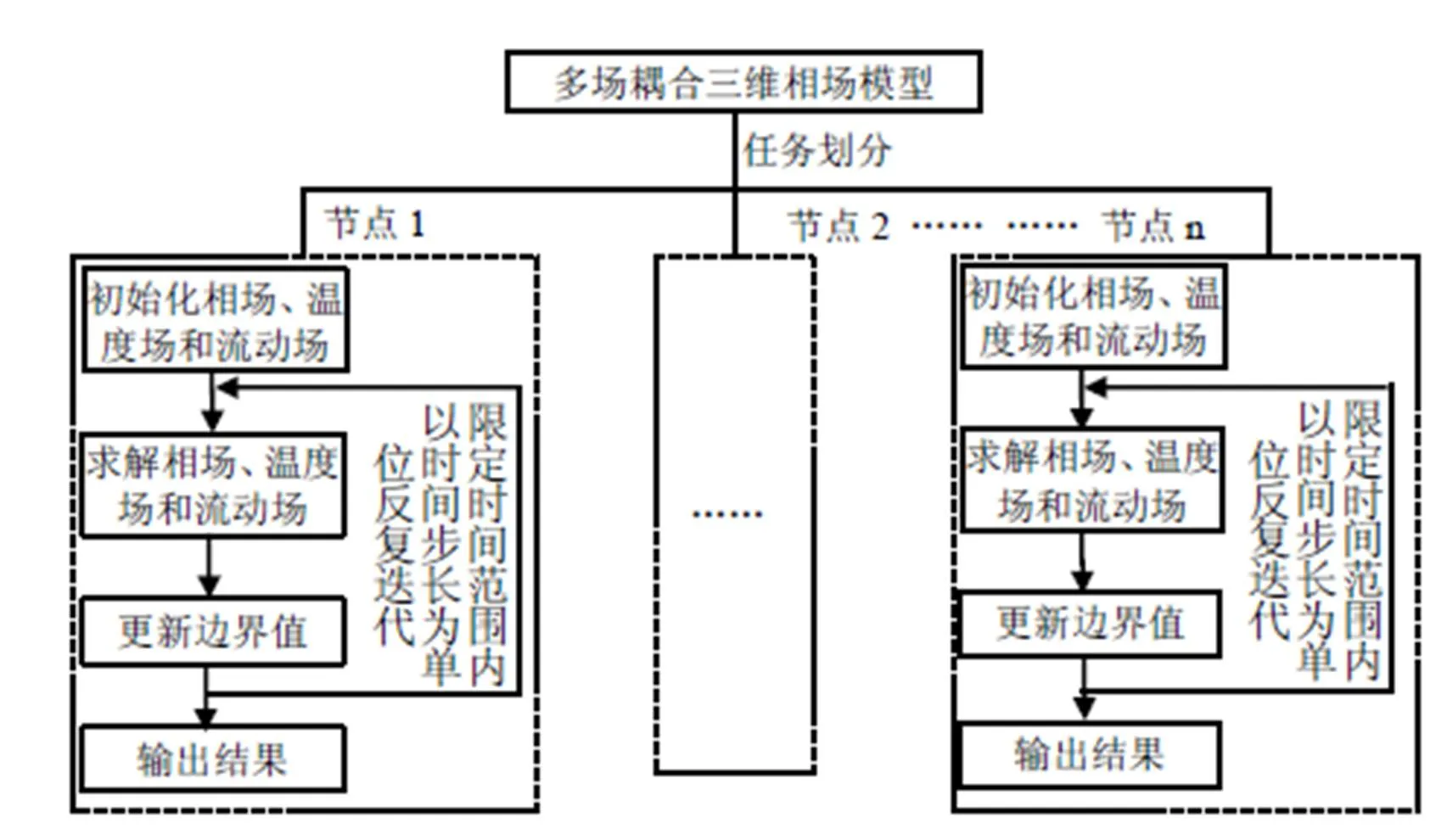
图1 MPI对等模式求解模式

图2 MPI并行模拟结果
图2(f)为图2(e)对应的温度场形貌切片。发现流动的存在破坏了温度场边界层一致的厚度。因为枝晶凝固过程是不断释放潜热的过程,流动的冲击带走了上游侧的热量,而熔体的过冷度是枝晶凝固的驱动力,从而上游侧枝晶在凝固过程释放的潜热能够快速扩散,温度边界层厚度较薄,加快了上游侧及法向上游侧枝晶生长速度;下游侧潜热因受已凝固枝晶的影响不容易扩散,温度较高,不容易凝固,温度边界层相对上游侧也更厚。上述原理均与串行情况下及理论上流动对枝晶生长影响机制一致,同时也证明了文中采用MPI并行算法的正确性和有效性。
3.2 MPI并行求解效果分析
MPI并行技术被广泛应用在需要扩大求解规模的问题领域中,本文中采用对等模式,每个进程负责求解的计算量完全相同。文中模拟的三维多场耦合相场模型串行程序在单机上模拟区域上限为1703,通过MPI并行后可扩规模到3203。图3为求解区域网格数大小为1703,其他所有参数都相同的情况下,MPI在不同进程数时相对于串行程序的加速效果。从图3可以看出,当启动进程数从8~10过渡时,加速效率没有呈明显上升趋势,进程数增加为12时,加速效率反倒有点下降,经测试中间进程,当进程数为9时,MPI并行程序取得最大加速比9.62倍。其主要原因在于:当启动较少进程时,各进程间边界数据交换较少,数据通信时间短,加速效率较明显;随着进程数的增多,划分的子任务更多,边界数据通信时间也随之延长,计算时间无法隐藏通信时间,从而导致效率下降或持较平稳趋势。
4 结论
(1)本文基于MPI技术对PF-LBM三维多场耦合相场模型进行了并行求解,进一步理解了流动在三维相场模型中对枝晶生长过程的影响。
(2)结果表明MPI并行技术不仅可以扩大计算规模,也可以在同条件下获得较高的加速比。
(3)文中并没有充分利用节点计算资源,后期将结合粗细粒度混合并行进一步提升模拟效果。
[1]刘卫津. NiCu合金枝晶生长相场法模拟及关键技术研究[D]. 太原:中北大学,2014.
[2]侯蕊. 相场法模拟Ti-Al二元合金枝晶生长[D]. 沈阳:沈阳师范大学,2017.
[3]刘静,段萌萌. 相场模拟对流影响凝固组织形成的研究进展[J]. 铸造技术,2012,33(4):459-462.
[4]康永生. Fe-C合金枝晶生长过程的相场法模拟研究[D]. 太原:中北大学,2017.
[5]郭照立. 格子Boltzmann方法的原理及应用[M]. 北京:科学出版社,2009.
[6]KARMA A, RAPPEL W J. Quantitative phase-field modeling of dendritic growth in two and three dimensions[J]. Physical Review Letter,E,1998,57(4):4324-4349.
[7]吕星,杨湘杰,桂云鹏,等. 过冷熔体近球晶组织形成机理的相场模拟[J]. 铸造技术,2015,44(7):88-91.
[8]Q Li, K H Luo, Q J Kang, et al. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer[J]. Progress in Energy and Combustion Science,2016:62-105.
[9]Hyun Geun Lee,Junseok Kim. A simple and efficient finite difference method for the phase-field crystal equation on curved surfaces[J]. Computer Methods in Applied Mechanics and Engineering,2016:32-43.
[10]William L. George,James A. Warren. A parallel 3D dendritic growth simulator using the phase-field method[J]. Journal of Computational Physics,2002:264-283.
[11]Altenfeld R,Apel M,Mey D,et al. Parallelising Computational Microstructure Simulations for Metallic Materials with OpenMP[J]. Proceedings of IWOMP 2011,B.M. Chapman et al. eds,2011,6665:1-11.
[12]Aoki T,Ogawa S,Yamanaka A. Multiple-GPU scalability of phase-field simulation for dendritic solidification[J]. Progress in Nuclear Science and Technology,2011,2:639-642.
[13]Yamanaka A,Aoki T,Ogawa S,et al. GPU-accelerated phase-field simulation of dendritic solidification in a binary alloy[J]. Journal of Crystal Growth,2011,318(1):40-45.
[14]Shimokawabe T,Aoki T,Takaki T,et al. Peta-scale phase-field simulation for dendritic solidification on the TSUBAME 2.0 supercomputer[C]. Proceedings of the 2011 ACM/IEEE International Conference for High Performance Computing, Networking,Storage and Analysis,2011:1-11.
[15]HE N Z,WANG N C,SHI B C,et al. A unified income-pressible lattice BGK model and its application to three-dimensional lid-driven cavity flow[J]. Chinese Physics,2004,13(1):40-46.
Research on Parallel Method of LBM Three-Dimensionalphase-Field Model
Jia Jinfang Xue Wandong Deng Xin Cao Tengfei Feng Li Yang Pei
Computer Technology and Application Department, Qinghai University, Qinghai Xining 810016
In the paper, taking high purity Succinonitrile as the research object, the three-dimensional dendritic non-isothermal growth PF-LBM phase-field model coupling flow field is parallel computed based on MPI, which solves the problems of large computational capacity, long computation time and small simulation scale. The results show that MPI parallel solution can not only enlarge the simulation scale to some extent, but also obtain a higher acceleration ratio under the same conditions. The correctness and effectiveness of the MPI parallel algorithm are also illustrated by the same influences of flow on the three-dimensional dendritic growth process.
phase-field model; three-dimension; LBM; MPI
TG111.4
A
青海大学中青年科研基金项目(2015-QGY-13)。
通信作者为贾金芳(1991—),女,甘肃天水人,助教,硕士。E-mail:543860105@qq.com。

