农村饮水安全工程可持续运行管理绩效考核评价研究

(辽宁省辽阳市辽阳灌区管理处，辽宁 辽阳 111000)

我国政府关注的重中之重的问题就是“三农问题”，自2005年我国加强对农村饮用水安全问题的治理和资金投入以来，安全饮用水设施逐渐得到完善，全国已有80%的地区农村饮用水问题得到解决，且基本实现了农村安全饮用水设施的建设[1]。然而，长期有效的确保饮水工程设施的有效性和可持续性相对于农村安全饮用水工程设施的建设更具有挑战性和困难性。对其可持续运行管理进行绩效考核评价，是有效监督工程设施运行管理、促进可持续发展和生产效益的重要途径，对完善农村饮用管理运营机制和长期发展效益具有重要意义，有利于促进其实现可持续性的长远效益。当前，开展运行管理绩效考核的研究和方法相对较少，且多以层次法理论模型为主，对评价指标采用层次分析法进行计算，具有一定的主观性，其评价结果往往与实际状况产生较大的偏差；而且，对于所构建的评价指标体系，对管理绩效考核未能全面的考虑其可持续发展特征。综上所述，本文在充分考虑了管理体系中安全、经济、组织、工程管理、权重满意度以及可持续性能等六个参数指标的基础之上，并利用熵组合权重法对各评价指标进行权重系数的计算，基于灰色理论构建了用于管理绩效考核的灰色聚类评价模型，然后以辽宁省朝阳县为例，对其进行管理绩效考核评价分析，进而检验了模型的可靠性和适用性[2-5]。

1 构建熵组合赋权和灰色聚类模型

对于不确定性、非线性系统问题进行处理往往采用的方法是灰色聚类模型，本研究在构建了评价指标体系，并利用熵组合权重法对评价指标权重计算的基础之上，基于白化权函数基本理论构建了灰色聚类评价模型[6]。

1.1 评价指标集的建立

本文所构建的评价指标体系主要有目标层、一级指标、二级指标三个层级，其中各评价指标层级可采用集合U={U1，U2，…，Um}和Ui={Ui1，Ui2，…，Uim}进行表示，其中i=1，2，…，m，上述公式中一级评价指标总个数用m表示，对应于一级指标的二级指标的总个数用ni表示。

1.2 指标权重的确定

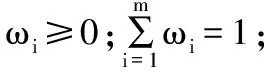
(1) 计算评价指标的主观权重系数。在对一级评价指标权重进行计算的基础上，可对各二级评价指标的重要性进行两两之间的对比分析，并构建互补性模糊判断矩阵Pi={Pikj}，且符合0≤Pikj≤1基本条件；当Pikj>0.5时代表评价指标k的重要性程度大于指标j，该值的大小代表了评价指标的重要性程度，各指标满足Pikj+Pijk=1；(i=1，2，…，m；k，j=1，2，…，ni)条件，其主管权重系数ω1ij可采用下述公式计算：

(1)

(2) 通过一致性检验对指标主观权重合理性进行判别。设定二级评价指标的主观权重向量为W1i=(ω1i1，ω1i2，…，ω1in)，并以P={Pikj}为权重向量的互补型模糊判断矩阵，其特征向量采用P*=(ω1ikj)ni×ni，并采用下式表述：

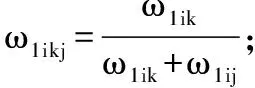
(2)

对指标的主观权重合理性采用P和P*的一致性进行检验，即采用相容性指标I对其判别，公式如下：

(3)

利用上述公式进行计算，指标的主观权重合理性取值范围为I<0.1。

(3) 对指标的客观权重进行计算。采用等权法对客观权重ω2ij计算，各评价指标的权重相等采用式ω2ij=1/ni进行判别。

(4) 对指标的组合权重进行计算。对主观和客观权重ω1ij、ω2ij进行组合权重计算，可到的最终的权重，且应尽可能的保持与接近，利用最小信息理论：

1.3 评价等级标准即样本矩阵的建立

对定性评价指标进行定量化计算，结合农村饮用水管理现状和可持续发展状况[7]，利用模型对运行管理绩效考核评价标准划分为优、良、合格、差和很差5个等级标准，所对应的各评价等级的取值区间范围分别为10～9,9～7,7～3,3～1,1～0。利用专家赋分法建立样本评价矩阵，若参与打分的专家为p个，则所构成的评价矩阵如下D=(dijh)(n1+n2+…，+nm)×p，其中第h位专家对Uij评价指标的赋分值采用dijh表达。

1.4 白化权函数的确定

灰色聚类理论计算的理论基础是白化权函数，根据文中所述的5个评价等级标准，可进行各等级分区及相应赋权的计算分析，进而确定各指标阀值和白化权函数，其中整个区间的中间点值至以及各区间的临界值即为阀值，其值分别为1、3、5、7和9，各等级区间的白化权函数计算公式分别如下所示：

(4)

(5)

(6)

(7)

(8)

1.5 二级指标灰色评价权的计算

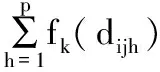
(9)

上述公式中采用rij=(rij1，rij2，rij3，rij4，rij5)表征指标Uij的灰色评价权重向量，其中i=1，2，…，m；j=1，2，…，ni。

1.6 一级指标的综合评价

对各一级评价指标进行综合性评价，设定Bi为对应于一级评价指标Uij的灰色综合评价向量，用下式表示：

Bi=WiRi=(bi1，bi2，bi3，bi4，bi5)

(10)

上式中：Wi=(ωi1，ωi2，…，ωin)；

(11)

上述公式中：Wi为对应于二级评价指标Uij的权重向量；Ri为rij向量构成的各指标的评价矩阵。

1.7 灰色综合评价的总评价目标

对模型目标层指标U进行总目标的评价，并以B为总评价目标U的灰色综合评价向量，表达式如下：

B=WR=(b1，b2，b3，b4，b5)

(12)

上述公式中：W=(ω1，ω2，…，ωm)；R=(B1，B2，…，Bm)；W为总目标层的下级评价指标的权重向量。

利用向量B进行单值化处理可得总目标U的灰色综合评价值C，表达式如下：

C=B(λ1，λ2，λ3，λ4，λ5)T=b1λ1+b2λ2+b3λ3+b4λ4+b5λ5

(13)

上述公式中：λk为各评价指标的阀值，分别为1、3、5、7、9。

对各指标的灰类白化权fk(C)进行计算，其中C仍为灰度，基于最大白化权基本原则，当fi(C)=max{fk(C)}(1≤k≤5)时，可对评价目标U进行第i的灰类判定，其中第i的灰类的等级即为评价等级。

表1 辽宁省朝阳县农村饮用水管理绩效考核指标体系

2 基于辽宁省朝阳县的考核评价指标体系

构建及计算

本研究基于辽宁省朝阳县社会经济发展状况、管理特点、供水现状以及小康社会建设基本要求，并基于国家有关运行管理规定、考核办法以及指导意见[8]，在参考相关文献和专家经验的基础上，构建了管理考核评价指标体系，如表1所示。

首先根据专家对不同评价指标之间进行对比计算，并构建互补判断矩阵，其中一级指标和二级指标的互补判断矩阵P的计算结果如下：

对系统相容性指标I利用公式(2)(3)进行计算，其计算结果为(0.0275；0.0320；0.0285；0.0450；0.0261；0.0123；0.0426)，各值均不大于0.1，表明各层级测评价指标主观权重表现出良好的合理性。利用相关公式对评价指标体系进行各指标的组合权重计算。

按上述计算方法对各二级指标的评价权进行计算，可得到各二级指标U11的评价权，然后基于各二级指标的评价权，可得到对应于指标U11的灰色评价权向量r11=(0.167，0.201，0.240，0.218，0.171)，同理对其他各二级指标进行计算并汇总，最终各一级得到灰色综合评价矩阵Ri；然后根据各指标的权重利用公式(10)可进行二级指标的权重向量，计算结果为：

B1=W1R1=(0.142，0.171，0.201，0.224，0.258)

B2=W2R2=(0.155，0.182，0.210，0.202，0.237)

B3=W3R3=(0.167，0.191，0.224，0.205，0.201)

B4=W4R4=(0.158，0.182，0.211，0.187，0.263)

B5=W5R5=(0.172，0.183，0.241，0.187，0.203)

B6=W6R6=(0.150，0.180，0.211，0.216，0.238)

最后，利用公式(13)对B进行单值化处理，最终可得到总目标U的灰色综合评价值C，C=(0.158，0.182，0.217，0.218，0.240)(9，7，5，3，1)=4.602，经过计算可得f1(C)=0.508、f2(C)=0.661、f3(C)=0.918、f4(C)=0.769、f5(C)=0.658，根据等级评判标准可知，朝阳县绩效管理考核处于合格水平。综上所述：评价指标体系中一级评价指标的权重有大到下依次为组织、安全、可持续能力、工程、满意度和经济管理。其中在工程运行管理中，组织管理是最为重要，因此做好组织管理是确保工程正常运行的关键性条件；安全与人民生命财产息息相关，需对安全管理引起足够的重视；而可持续发展是解决农村饮用水问题长久性的重要支持，故仍需重点加强和关注；满意度、工程和经济管理三项指标是保证饮水工程效益和长久性发展的必要条件[10]。

3 结语

本文结合研究区域饮用水管理基本现状和国家相关制度政策，在详细分析了熵权组合和灰色聚类理论的基础之上，构建了用于评价辽宁省朝阳县农村安全饮水可持续隐形的绩效管理评价模型。研究表明：朝阳县农村饮用水安全可持续管理处于合格水平，所构建的评价模型能够较为准确、客观对绩效管理水平做出评价，评价结果与实际状况保持高度的一致性，表现出良好的精确性和可使用性。