基于单视影像的相似材料模型位移监测研究

段志鑫，吴 侃，白志辉，李 亮，周大伟，王 瑞，3

(1.中国矿业大学 环境与测绘学院，江苏 徐州 221116；2.冀中能源峰峰集团有限公司，河北 邯郸 056000；3.江西理工大学 应用科学学院，江西 赣州 341000)

相似材料模拟实验是研究复杂地质和岩土工程问题的重要手段，它可以较为直观地反映所模拟工程原型的物理力学性质和岩层运动规律，由于具有观测周期短，成本低，结果直观等优点，被广泛地应用于采矿和边坡工程等研究中[1-2]。位移监测是相似材料模拟实验的主要观测内容，也是对岩层运移规律和破坏特征进行分析的数据基础。目前，相似材料模拟实验中位移监测的方法包括：百分表法、灯泡透镜法、精密水准法、近景摄影测量法、光纤光栅传感器监测法以及三维激光扫描法等。其中，百分表法和精密水准法测量精度较高，但是只能监测某一个方向上的位移[3]；灯泡透镜法的测点精度可以达到0.2mm以内，但是在布点较多的情况下，测量效率较低，难以保证动态观测[4-5]；光纤光栅传感器法观测成本较高，且容易对模型的自身形变造成干扰[6]；三维激光扫描方法的点位测量精度较低并且数据量大，不便于后期处理[7]；近景摄影测量法应用较为广泛，但是每次观测需要拍摄多张照片且易产生噪声点，不利于实现动态观测[8-9]。

近年来，众多研究者对基于单张图像的变形监测方法进行了大量研究，提出了数字散斑图像[10]、亚像素圆心检测[11]等方法。在这些方法中，标志点的提取始终是获取高精度的形变量的关键。为了实现对相似模型岩层形变量的高效、精确监测，本文拟提出一种基于阈值分割和局部边缘检测的最小二乘椭圆拟合法，提高单视图像中标志点中心的提取精度，并基于数字摄影测量的原理，对普通数字图像进行畸变校正、空间变换等处理，得到高精度的标志点中心坐标，进而通过对应点比较获取模型的形变量，为研究相似材料模拟实验中的岩层内部移动及破坏规律提供支持。

1 实验概况

本次实验的观测对象为模拟西部风积沙地质条件下采煤的相似材料模型，模型尺寸为宽3000mm，厚300mm，高1000mm，模型几何相似比为1∶150。根据相似材料模型岩层分布的特点及实验监测需求，在模型表面布设有14排测点。XJTUDP系统是基于工业近景摄影测量理论开发的近距离测量系统，系统单点点位测量精度可达0.03～0.1mm[12]。为了对实验效果进行对比验证，同时在模型表面及框架上布设若干XJTUDP近景摄影测量系统的方形编码标志点，实验中采用普通的数码相机对模型进行观测，每次观测时尽量保持正直拍摄，如图1所示。

图1 相似材料模型测点布设

2 数据处理流程

基于近景摄影测量和亚像素圆形检测法的相似材料模型位移监测方法的主要流程如下：

(1)进行相机标定并建立严格的畸变模型对采集的图像进行畸变校正，提高图像的几何精度。

(2)利用提出的最小二乘椭圆圆心检测方法获取标志点的中心坐标。

(3)利用DLT变换将测点坐标转换到物方坐标并获取模型形变量。

2.1 图像畸变校正

普通数码相机在成像的过程中都会存在一定程度的几何失真，即相机畸变，这些畸变误差会对照片的成像质量和标志点提取的精度产生影响，因此需要标定相机的畸变参数。目前相机标定的算法比较成熟多样[13]，本文使用MATLAB软件中的摄像机标定工具箱对其进行标定。标定结果见表1。

表1 相机畸变参数

利用相机的畸变参数，建立如式(1)所示的畸变校正模型，并由式(2)计算得到图像上每个像素的去畸变坐标。

(1)

(2)

式中，(Δx,Δy)为像点坐标偏差；(x，y)为像点实际量测坐标；(x0,y0)为像主点坐标；k1，k2，k3为径向畸变系数；p1，p2为偏心畸变系数；r为像点的畸变半径；(xu,yu)为像点去畸变坐标。

2.2 标志点中心检测

在近景摄影测量与计算机视觉检测中，常用的投影标志点有圆形标志点、扇形标志点、方形标志点等，本次实验中采用圆形标志点进行位移监测，如图2(a)所示。因此，对标志点圆域的准确提取，是保证标志点中心坐标精度的关键。目前常见的平面圆检测方法有边缘检测法、hough变换检测法、曲线拟合法等，其中边缘检测法精度较低且抗噪性较差[14]，hough变换检测法计算量较大并且对椭圆检测效果不佳[15]，曲线拟合法的拟合精度易受噪声影响[16]，而相似材料模型表面的标志点具有数量多、椭圆性、背景复杂等特点，如图2(a)所示，利用上述方法难以得到理想的检测效果。针对这个问题，本文提出一种基于阈值分割与局部边缘检测的最小二乘椭圆检测方法，实现对标志点中心的高效准确提取。

该方法的具体过程如下：

(1)利用大律法对模型灰度图像进行阈值分割，如式(3)所示，得到以标志点白色区域为前景的二值图像，如图2(b)所示，并根据连通域面积等准则滤除少量背景噪声。

(3)

式中，G(x,y)为二值图像像素灰度值；g(x,y)

图2 相似材料模型标志点中心检测

为原始图像像素灰度值；T0为大律法分割阈值。

(2)利用公式(4)计算二值图像上每个标志点连通域的质心坐标(u0，v0),并获取每个连通域对应的目标外接盒的长l，宽w。

(4)

式中，n为连通域的像素数；(ui，vi)为每个像素的坐标；g(ui，vi)为像素灰度。

(3)根据标志点的实际内径r与外径R的长度，利用公式(5)计算扩充比例系数σ，对连通域的外接矩形进行扩充，扩充后的矩形长宽为L，W。

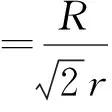
(5)

(4)在以连通域质心(u0，v0)为中心，扩充外接矩形的长宽为维数，在灰度图像上确定每一个目标标志点的检测区域，利用Canny边缘检测算子获取检测区域内白色椭圆的轮廓及其边缘点坐标(xi，yi)，结果如图2(c)所示。

(5)利用公式(6)对步骤(4)中检测得到的边缘点进行最小二乘法椭圆拟合，得到椭圆的圆心坐标(xc，yc)，即为标志点的中心坐标，如图2(d)所示。

(6)

式中，f为目标函数；A，B，C，D，E为椭圆方程的5个系数；N为边缘点个数。

2.3 标志点坐标变换

经过本文方法检测得到的标志点中心坐标为像方空间坐标，而不是实际坐标，无法直接对其进行位移分析，因此需要将标志点圆心坐标转换到物方空间。为了得到高精度的物方坐标，本文利用模型架上固定控制点建立直接线性变换模型，并基于Ceres-solver解算器对转换系数进行平差优化，进而得到最优的转换模型。

2.3.1 直接线性变换

直接线性变换(DLT)是通过直接建立目标点位的像方坐标与物方坐标之间的线性变换关系的模型[17]，该方法由于不需要事先测定相机的内外方位元素，因此被广泛地应用于非量测相机摄影测量中。相似材料模型监测中测点均布设在同一平面，因而只需要测量不少于4个控制点的实际坐标并采用二维的DLT变换求解出相应变换矩阵及其变换参数，进而将标志点坐标转换到物方平面，具体的变换模型如式(7)所示。

(7)

式中，(xu,yu)为标志点去畸变后像方坐标;(X,Y)为对应标志点物方平面坐标；L1～L8为二维DLT变换的8个参数。

2.3.2 基于Ceres-solver平差优化

Ceres解算器是一个开源的C++库，主要用于建模和解决大型、复杂的优化问题。Ceres解算器可以解决两类问题。一是求解有边界约束条件的非线性最小二乘问题，二是求解一般的无约束最优化问题。它仅需要建立合适的平差模型，根据需要选择最优的平差算法，即可快速有效地求解非线性最小二乘问题[18]。实验中挑选均匀分布的4个固定控制点，根据其像方坐标与物方坐标求取直接线性变换系数，并以此作为平差初值；然后基于Ceres-solver解算器，选择具有较强抗粗差能力的Cauchy-Loss平差函数对所有的固定控制点进行迭代平差处理，以得到最优的直接线性变换系数。对多期数据的共50个控制点进行直接线性变换误差统计，如图(3)所示。由误差曲线可知，未进行平差优化时，模型控制点的转换误差较大，最大误差已达2.5mm，在对转换系数进行Ceres-solver平差优化后，点位坐标转换误差有了明显减小，最大误差控制在1mm以内，可满足模型标志点解算的要求。

图3 模型控制点转换误差

3 实验结果及分析

3.1 标志点精度分析

在近景摄影测量中，由于受到相机光学畸变校正效果、摄影方式、像控点的数量及分布、像控点实测精度、图像分辨率、标志点中心提取精度等因素的影响，解算得到的标志点坐标会存在一定的误差。XJTUDP近景摄影测量系统具有较高的点位测量精度，为了检验本文方法提取相似材料模型表面标志点坐标值的精度，实验中以近景摄影测量系统获取的标志点坐标作为实测值，与本文方法解算得到的标志点坐标进行对比和误差分析。由于相似材料模型只考虑模型表面上的二维形变，因此实验中只对标志点的x，y坐标值进行分析。随机选取8个点进行坐标值误差统计，如表2所示。

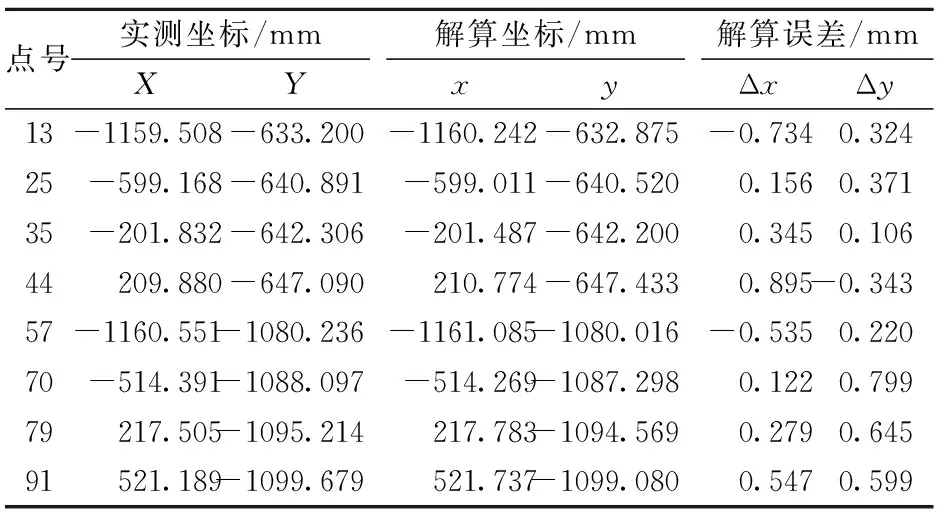
表2 标志点坐标解算精度分析

综合所有的检查点，按照公式(8)计算本文方法得到的标志点在X，Y方向上坐标值的中误差分别为：mx=0.520mm，my=0.479mm。XJTUDP系统点位测量误差最大为0.1mm，考虑该系统自身误差，本文方法在X，Y方向上点位坐标测量误差小于0.620mm。目前相似材料模拟实验中，模型几何相似比通常为1/200～1/50，相似比太大可能会掩盖掉模型形变的细节，相似比太小会将点位观测误差放大。本文实验中模型几何相似比为1∶150，因此，对应实际监测点在X，Y方向的绝对中误差均小于93mm。本文方法监测精度优于三维激光扫描法，且在监测效率及简便性上较其他方法更为突出，可以满足一般相似材料模型监测的要求。

(8)

式中，m为中误差；Δ为误差值；n为观测值个数。

3.2 模型形变分析

为了验证本文方法在实际相似材料模型监测中的可靠性，基于单视影像解算出每一次开采前模型表面的标志点坐标，并计算对应点的位移量。选取模型开采500mm，1000mm，1500mm，2000mm的模型地表标志点位移数据，绘制模型地表下沉曲线，如图4所示。由地表下沉曲线可以看出，随着模型工作面的推进，模型地表的下沉量不断增大，开采2000mm后，模型地表下沉量达到最大，为26.37mm，最大下沉量出现在下沉盆地中心，且下沉盆地中心随着工作面的推进方向移动。总体而言，下沉曲线的位移规律性较好，其中位移变化、下沉盆地、开采影响范围等观测内容与现场实验过程中观测到的基本一致，且符合对模型的定性分析判断。因此，本文方法得到的相似材料模型形变量是可靠的，可以基本反映相似材料模型采动过程中地表及覆岩层的位移变化规律。

图4 模型地表下沉曲线

4 结 论

(1)本文对基于单视影像的相似材料模型形变量监测方法进行了研究，通过影像畸变校正、标志点精确提取、DLT变换及平差优化等步骤，解算得到了相似材料模型标志点的物方坐标并计算了模型地表的下沉曲线。

(2)试验研究表明，本文方法在X，Y方向上点位坐标测量误差小于0.620mm，可以较为准确高效地获取模型的形变量，且观测成本低、便于连续实时观测，能够为相似模拟实验提供丰富的位移场与特征图像数据，对于矿山开采沉陷等岩土模拟研究具有一定的实用价值。

(3)由于本文方法尚处于试验阶段，因而算法及数据处理的模块化和自动化程度还需进一步提高。