电极驱动微槽道流动的高电压边界数值模拟①

,

(北京航空航天大学航空科学与工程学院，北京 100191)

0 引 言

随着芯片实验室技术快速发展，如何在微米的尺度上驱动流体流动有了迫切的需求。传统的通过压力梯度驱动的方式在流动尺度很小的情况下有流量小的缺点，所以通过其他技术来驱动槽道中流体流动得到大量的发展。电场驱动流动的流量与管道直径的平方是正比关系，同时在电渗流动中流速剖面沿管道横截面均匀分布，减小泰勒弥散效应[1]，因此电驱动比压力驱动在微流动中应用广泛，更深入的研究电驱动MEMS 对于流体流动的控制效果有利于更好地应用流动控制。

近年来，电极驱动的微槽道流动有两种电极布置方式：施加相同的交流信号的非对称布置电极和多个等宽度电极上施加相同相位差的行波信号(如图1)。Ramos等人对这两种不同的电极布置方式进行了实验，并且提出了基于Debye-Huckel 双电层理论的线性模型[2]。大部分的研究者选择应用此线性模型进行研究，如Hung-ChunYeh等人在此线性模型的基础上计算了在微槽道的上下壁面都布置电极的情况[3]和Kuan-RongHuang等人将行波电渗流应用于微流体混合[4]。

等宽度电极行波驱动的微流动电渗流的物理模型如图1，在微槽道流动中，槽道的上下壁面上安装电极，在双电层中聚集的正负离子由电极产生的行波信号所驱动。由于电极表面充电的时间是有限的，诱导的离子分布延迟于行波[5]。这种非均匀的电场诱导双电层中的离子运动，从而通过粘性驱动流体沿着行波的方向运动。

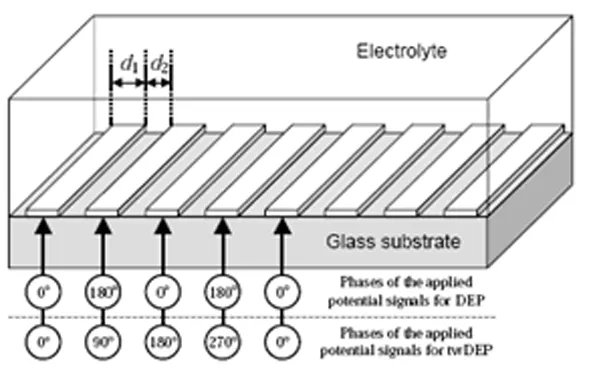
图1 行波驱动电极分布示意图

目前电极驱动的微槽道流动实验结果是在比较大的边界条件下做的，但是大部分的数值算法都是基于线性动电学模型，比如可以通过electrical circuit theory的电容-电阻-电容(CRC)电路进行近似求解，双电层像电容一样储存电荷，同时电解质溶液作为电阻存在。但是由等价CRC电路发展的理论只适用于电压低于热压RT/F(R是气体常数，T是绝对热力学温度，F为法拉第常数)的情况，在25℃其为25.7mV。而基于Poison-Nernst-Planck和Navier-Stokes方程(PNPNS model)的数学模型可以预测到实验中观测到的现象，比如倒流。根据相关研究[6,7]，PNPNS模型可以在电压振幅大于几百mV时得到物理相符的结果。因此，采用了直接数值模拟，配合高精度的谱方法对基于PNPNS模型的电极驱动二维微槽道流动进行数值模拟，实现在较大电压幅值条件下进行模拟。

1 数值方法

采用了与文献[8]相似的近似方法。数值方法基于以下的假设：1)等温的环境；2)稀溶液；3)无电极反应；4)固体表面无滑移；5)溶液连续不可压。在只考虑稀溶液时，不同离子的传递不相互影响，所以在建立溶质的扩散方程时就不考虑其他溶质的影响，使方程更简单。假设电极与溶液没有发生的化学反应。

在槽道的上下壁面安装电极，并假设电极足够多，可以将壁面上的行波视为理想的正弦波型。槽道高度为2H，溶液为KCl稀溶液，且假设正负离子摩尔密度相同。初始时刻在上下壁面电极上施加φ(xi)=A·sin(kxi)的电压，且随时间作正弦变化φ(xi,t)=A·sin(kxi-wt)。A为电压幅值，k为沿X轴相变率，k=2π/L，L为行波波长，w为角速度。对于已经完全发展的行波驱动微槽道流动，在流向上可以看作周期变化的，出口采用周期边界条件，同时X方向上计算域只取一个波长的长度，可以简化计算，加快计算结果收敛。

离子溶液为浓度为0.1moL/m3的KCl离子溶液，温度为25℃，介电系数为ε=80×8.854×10-12F/m，H=2μm。特征电压φ*=RT/F，在25℃是为25.7mV，特征长度L*取上下两平板的间距的一半为H/2，特征时间t*=H2/D，特征速度V*=H/t*=D/H，特征压强p*=ρV*2，特征浓度c*取远离壁面溶液中溶质的浓度和∑|ci|，D为离子扩散率。于是各个无量纲量为：

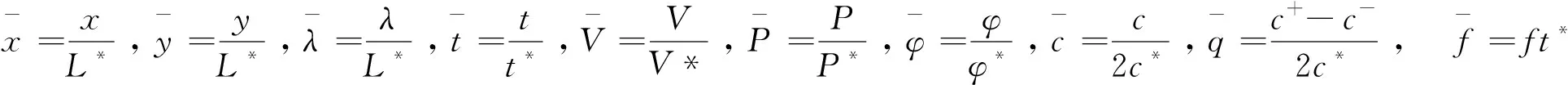
1)电势Poisson方程

(1)

边界条件

(2)

(3)

2)物质输运Nernst-Planck方程

边界条件为法向无穿透：

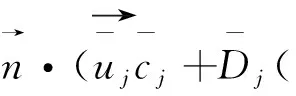
(5)

3)Navier-stokes方程

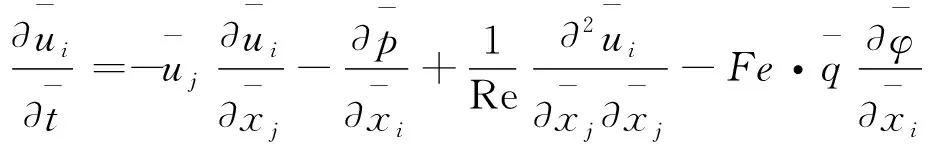
(6)

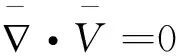
(7)

其中，Re=ρV*L*/μ，Fe=Fc*φ*/p*

边界条件为：

(8)

用时间推进格式采用了Karniadakis，Israeli和Orszag在1991年针对牛顿流体槽道湍流的直接数值模拟提出的高阶时间分裂格式，采用了二阶精度。

数值方法使用谱方法。谱方法具有很高的精度，槽道不可压流的计算结果表明，为了达到32个节点的Chebyshev谱的精度，需要布置接近10000个有限差分网格节点[8]，因此使用谱方法提高计算精度。采用的谱方法是Galerkin-Tau方法，即在流向采用Galerkin方法，在法向用Chebyshev -Tau方法。在时间分裂推进方法中，求解N-S方程时，粘性步只满足了避免无滑移条件，而没有连续性方程的约束，在经过粘性步之后，速度场会出现残余散度，需要使用影响系数矩阵的方法对散度进行修正，在流向和法向上利用3/2规则消除混淆误差。

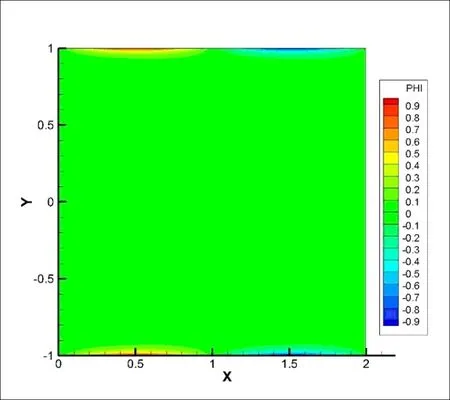
图2 A=1时电势云图

2 计算结果

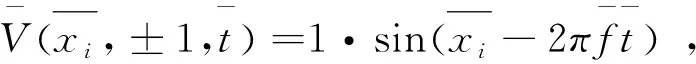
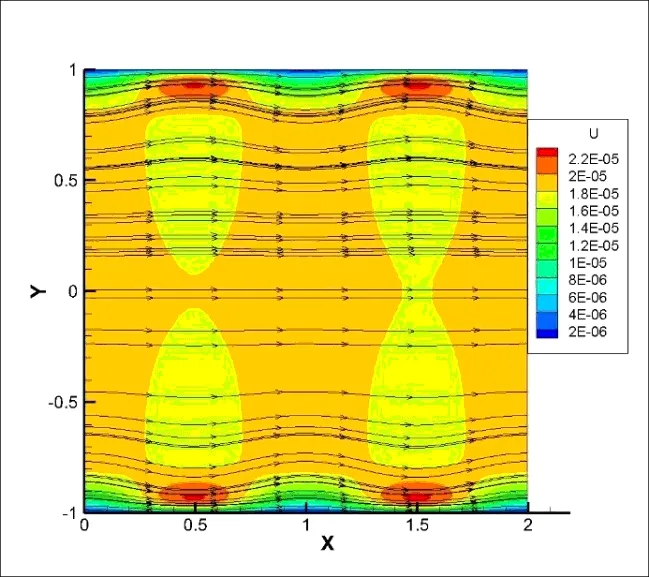
图3 A=1时流线与流向速度云图

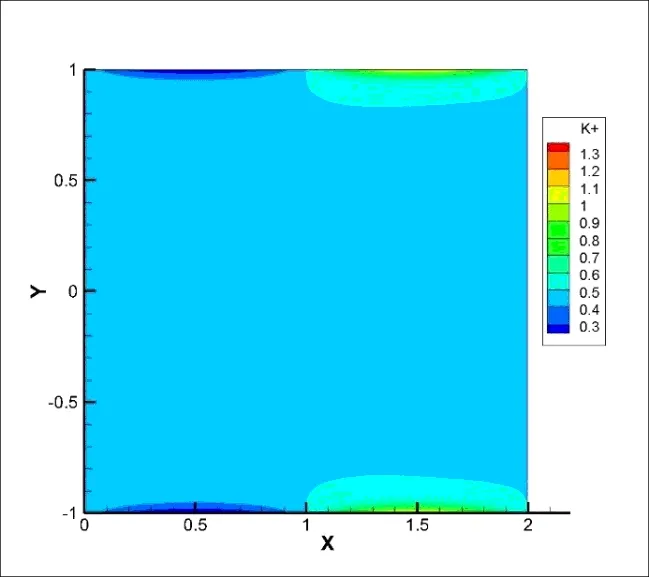
图4 A=1时K+ 离子浓度分布云图

图5 A=10时电势云图

由1增大到10，结果如图5～7：

图6 A=10时流线与流向速度云图

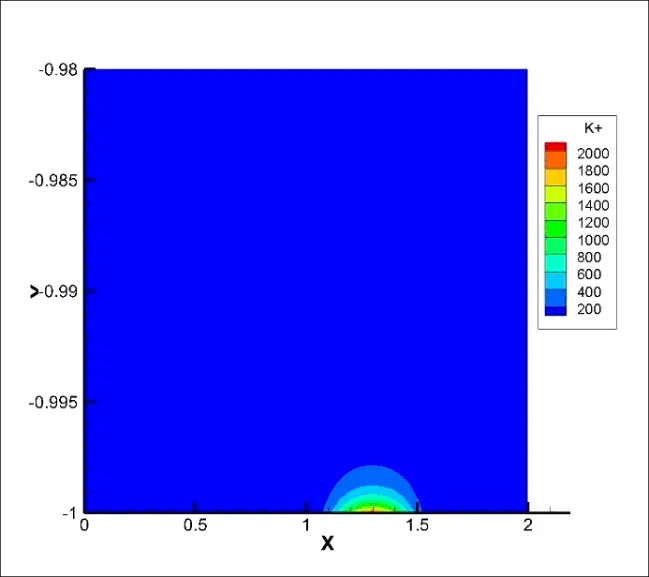
图7 A=10时K+离子浓度分布云图

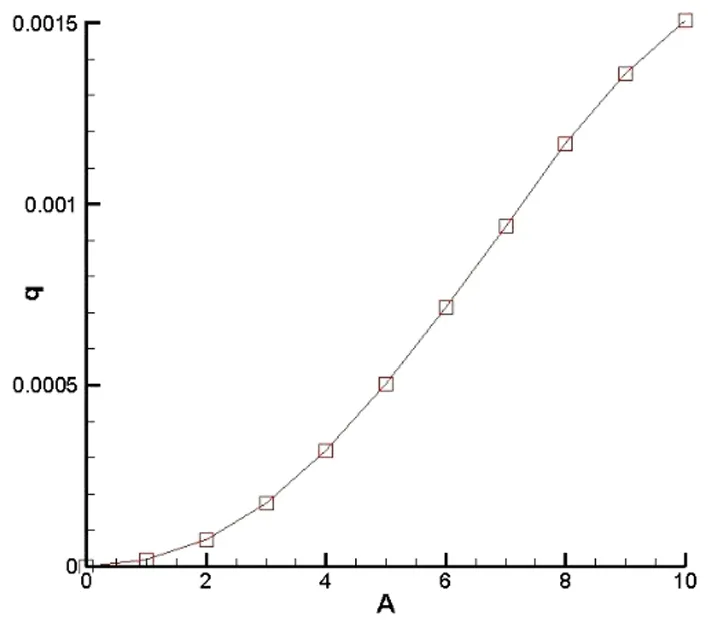
图8 流量随电压幅值A变化曲线

对比图5和图2，A= 10和A= 1的电势云图相识。对比图6和图3可以看到，在A= 10时比A= 1时流场流速明显增大。同时对比离子浓度分布云图的图7和图4，图7只显示了(-1，-0.98)区间内的离子浓度，在A= 10时溶液中的离子基本集中到了壁面附近，其他区域接近为零，K+离子比A= 1时更加的集中于壁面附近。

在基础电压由0逐渐增大到10，由图8可以得到，流量也随之逐渐增大，增长的速度逐渐增大，可能是由于随着边界条件电压的增大，电场强度也会随之增大，流速和流量也随之增大。

3 结 论

对于微槽道流动的物理模型通过PNPNS模型结合相应的边界条件使用谱方法进行离散，时间推进使用Orszag等提出的高阶时间分裂格式进行求解。对于二维的行波驱动问题，对边界条件行波的幅值由1逐渐增大到10的情况进行了计算，在高电压的情况下，PNPNS模型的计算结果仍然可以较快收敛， PNPNS模型可以用于计算较高电压的情况。