基于信息熵的动力模型缩聚中主自由度优化选择研究①

, ，

(武汉大学土木建筑工程学院，湖北 武汉 430072)

0 引 言

许多的桥梁工程以及高层建筑等结构在投入使用的过程中都会出现一些局部的破损,随着时间的推移，各种因素的影响会使局部破损不断扩大,造成整个结构的破坏[1]。在工程实践中，由于条件限制，为了能更好的对工程结构进行检测和维护，要将有限的传感器布设在结构的主要部位，获取更为全面的信息。

国内外学者对于传感器的优化布置问题提出了多种优化算法，Guyan[2]模型缩聚法是一种常用的传感器布置方法，Kammer[3]提出了传感器优化布置的有效独立法。在国内，崔飞[4]提出了模态置信度法，根据经验和初算来拟定一组测点，然后从剩余的自由度中每次增加一个测点，以此减小MAC矩阵中非对角元的最大值，来达到测点优化的目的。

针对桁架桥梁结构模型，运用动态模型缩聚法进行主自由度的优化选取，以桥梁建模参数识别结果的不确定性最小为准则来优化选取主自由度，对该桥梁结构模型进行数值仿真研究以及实验验证。

1 动力模型缩聚

有一类别的模型，假设有N个自由度，假如质量矩阵由于结构损伤的改变可以忽略，可以得到系统方程如下[5]：

K(θ)=λjMφj

(1)

其中，λj,φj∈RN,j=1,2,…Nt是方程的特征值和特征向量。Nt是测得的模态阶数。K(θ)是参数化之后的整体刚度矩阵，其中θ=[θ1,θ2,…,θNθ]T∈RNθ:

(2)

当θ=θ0时，代表结构处于健康状况下；K(i),i=1,2,…Nθ是组装成整体刚度矩阵的单元刚度矩阵的扩阶矩阵；Nθ是待识别的结构参数的个数。

将上述公式联合，并区分主副自由度，可以得到以下振动方程：

(3)

其中{φm}j和{φs}j分别是第j阶振型测得的和未测得的部分，维度分别是Nm和Ns,且有Nm+NS=N。

根据公式(3)可得：

{φs}j=Dj{φm}j

(4)

(5)

其中Dj是第j阶模态的动态缩减矩阵，是关于λj和θ的函数，如下：

(6)

(7)

因此，对于第j阶振型，可以只用主振型表示如下：

(8)

其中Tj∈RNNm是第j阶模态的转换矩阵，INm∈RNmNm是单位矩阵。

将公式(7)带入公式(3)，并且方程两边同时乘以T矩阵的转置矩阵得到：

(9)

其中：

(10)

(11)

(12)

(13)

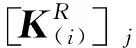
(14)

根据公式(11)可得[6]：

A(θ)θ=b(θ)

(15)

其中：

(16)

(17)

且有：

(18)

zj=zj(λj,{φm}j,θ)=

(19)

根据公式(15)可以得到：

θ=A(θ)+b(θ)

(20)

公式中的A(θ)+是A(θ)矩阵的伪逆矩阵，给定θ初始值θ0，k=1，每步迭代结果为θk=A(θk-1)+b(θk-1)，当两代θ之间的改变值小于一个指定的极小值，则迭代结束，θk为识别结果，否则迭代继续。

2 主自由度优化选取理论

2.1 贝叶斯理论

假设选取特定的某一类模型，模型中存在着结构自由参数，假设模型参数向量为θ，利用贝叶斯统计方法根据时域内的动力实验数据，推得结构的合理参数和不确定性。

将测得的实验数据记为D={y(m),z(m),m=1,…,N}，y(m)∈RN0,z(m)∈RNT分别是输入和输出数据。N0表示结构观测自由度的个数，NT表示输入自由度的个数，m表示时间指数mΔt,mΔt表示采样时间间隔，N表示采样数据的个数。当选定一类模型后，就可以获得模型响应输入与输出之间的关系[7]：

y(n)=L0q(m;θ)+n(m;θ)

(21)

以下假设预估误差对于不同的测量数据满足∑=σ2I，σ是预估误差参数，I∈RN0N0是单位矩阵。根据贝叶斯系统识别理论，随机的参数向量φ和测量数据D，得到模型参数θ的先验概率密度如下：

P(ψ,θ|M)=P(ψ|θ,M)P(θ|M)

(22)

其中：

P(θ|M)=N(θ0;Eθ)

(23)

先验概率密度函数如下[8〗：

(24)

其中c是常数，使得证据因子函数积分为1，而且有：

(25)

Σ=[(Σ1)T,(Σ2)T,…,(ΣNt)T]T

(26)

公式(26)中的Σj表示振动方程中第j模态向量的误差：

(27)

根据上文可得：

(28)

同理，可以得到模型修正后的后验概率密度函数：

P(ψ,θ|D,M)=c2P(D|ψ,θ,M)P(ψ,θ|M)

(29)

由此可得：

(30)

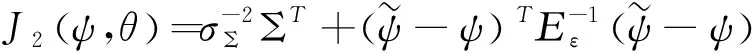
(31)

2.2 信息熵理论

修正的概率密度函数表示模态参数每个可能值的概率，根据测得的动力数据可以得到参数值的不确定性。信息熵作为唯一量测结构模型参数θ的不确定性的工具，表达方式如下[9〗：

H(δ,D)=Eθ[-lnp(θ|D)]=

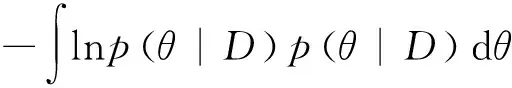
(32)

其中Eθ表示关于θ的数学期望。信息熵理论取决于测得的动力数据D和选取的主自由度δ。

根据C. Papadimitriou提出的理论可以得到信息熵理论[10]：

-Eθ[lnπθ(θ)]

(33)

(34)

(35)

(36)

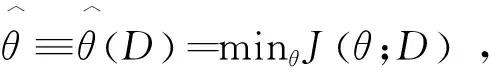
(37)

(38)

s/s0的值越小表明选取的主自由度组合越优，对于同一结构不同数量的主自由度组合s/s0也可以进行比较。

3 主自由度优化选取

3.1 MATLAB有限元建模及其验证

采用自编MATLAB程序建立简单的桁架桥模型。其中纵梁采用T型截面，横梁采用工字型截面，弹性模量为2.06×1011kN/m2，剪切模量为7.923×1010MPa，截面面积为0.904×10-3m2,y轴惯性矩为0.145×10-5m4，z轴惯性矩为0.21×10-6m4，泊松比为0.3，材料密度为7850kg/m3。如下图1所示：

图1中所示为桁架桥ANSYS模型图，4个端节点固支。采用ANSYS与MATLAB软件对该桁架桥建模并进行模态分析，求得前五阶模态参数。

表1 MATLAB与ANSYS计算频率(Hz)对比

图1 桁架桥ANSYS模型图

其中表1为频率结果，图2为振型结果，蓝色线代表的是桁架桥原位曲线，红色线和黑色线分别为MATLAB和ANSYS提取的振型结果。从表1以及图2的模态结果对比，可以看出两种软件结果吻合较好，充分说明所建模型的准确性。

3.2 主自由度优化选取仿真研究

上图3为桁架桥模型下部的示意图，根据结构对称性以及振型特点，将节点的竖向自由度作为主要自由度，故可选取的主自由度为1-18号节点的竖向自由度。待识别建模参数取为桁架桥下方前八个纵梁单元的刚度矩阵，共8个。采用遗传算法分别获得6和8个主自由度组合时的优化结果，并采用穷举法验证，因组合数较多，不列表显示。

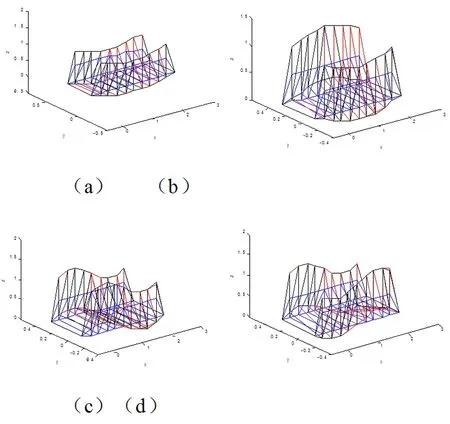
图2 MATLAB与ANSYS前四阶振型结果

图3 桁架桥主自由度示意图

为进一步验证，主自由度优化结果的正确性，选取部分不同的主自由度组合与优化得到的主自由度组合，进行损伤识别结果对比；一共各选取4种非最优组合，以下是6个主自由度组合识别结果对比：

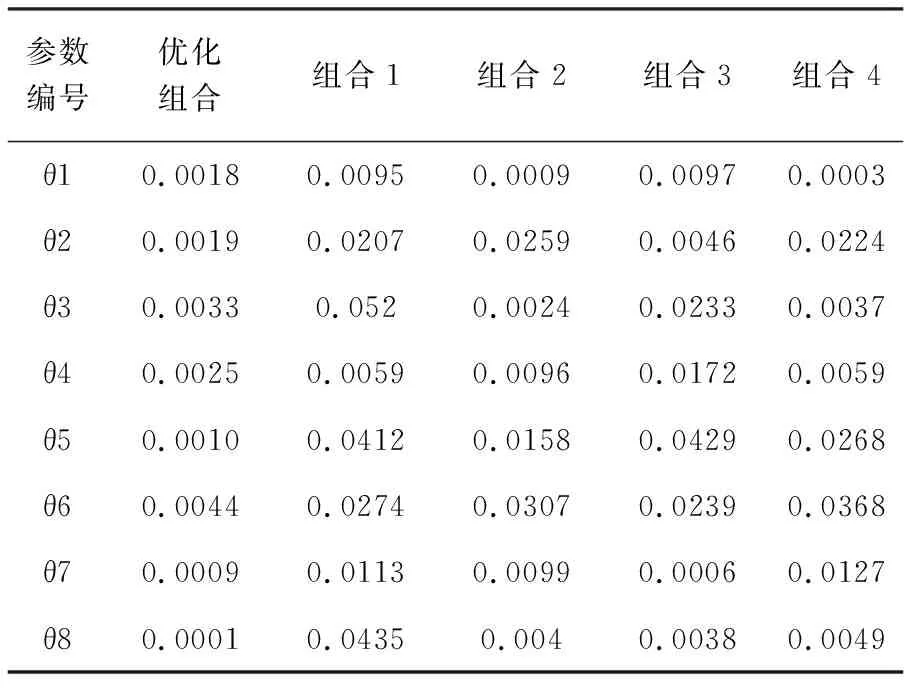
表2 6个主自由度的各参数识别结果的标准差

将表2中的结果绘制成图，如下图：

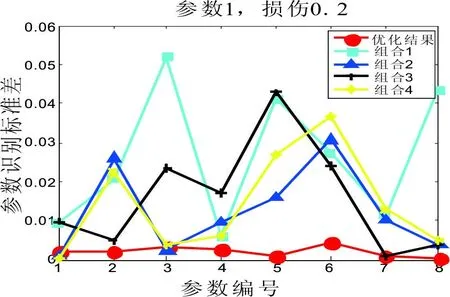
图4 6个主自由度的参数识别结果标准差

上图4中红色线为优化得到的主自由度组合，其余为非最优组合。从图4中可以看出，除了极少数的参数标准差偏大之外，优化得到的主自由度组合识别结果标准差绝大部分都是最小的，也就说明，这个主自由度组合更优，参数识别结果的不确定性最小。其中主自由度的编号为2、22、32、42、47、52〗，也即是下图中红色箭头所标注节点的竖向自由度组合，如图5所示。

图5 6个优化的主自由度组合示意图

图6 8个主自由度组合的参数识别结果标准差

以上给出主自由度个数为6时的最优主自由度组合。为进一步说明结果的正确性，将主自由度的个数定为8个，也对应选取4种不同的主自由度组合进行对比，识别结果如下：

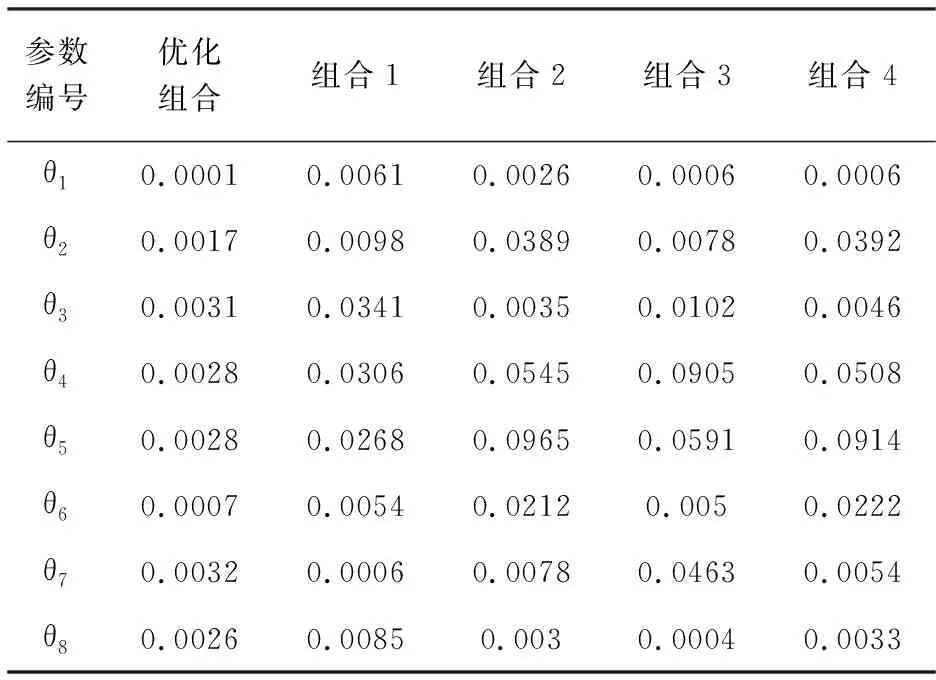
表3 8个主自由度的各参数识别结果的标准差

将表3中的结果绘制成图，如下图：

上图6中每条曲线的含义同图4相同，红色线为遗传算法优化得到的主自由度组合，其余为任意选取的与之对比的主自由度组合。每个参数的标准差越小，表示识别结果更稳定，不确定性更小。根据上文给出的结论，可以得到，优化得到的主自由度组合识别结果标准差绝大部分都是最小的，也就说明，这个主自由度组合更优；此种主自由度组合下各个自由度编号为2、12、22、27、47、52、82、87，如图7所示，红色箭头所标注节点的竖向自由度组合。

图7 8个优化的主自由度组合示意图

图8 (a)桁架桥模型 (b)实验装置系统

为进一步分析主自由度对比选取的结果，将上文中设置的两种工况，分别选定6个和8个主自由度的优化组合结果进行对比如下表4所示，从表4中可以看出主自由度的选取个数增加会使s/s0的值变小，说明随着主自由度个数的增多，计算中结构的所包含的信息量逐渐增大，这也说明结构中待识别建模参数识别结果的不确定性逐渐减小。

表4 桁架桥两种工况下计算结果表

3.3 实验验证

该桁架桥模型的几何参数与第一节给出的数值仿真参数一致，符合工程设计，以下为实验室桁架桥模型以及实验装置系统，如图8(a)和(b)所示：

实验室桁架桥模态提取试验采用的实验装置系统主要有桁架桥模型、数据采集仪(KT6016)，N-Modal模态分析软件、IEPE型加速度传感器(KT11000L)、冲击锤、笔记本电脑以及若干导线等。

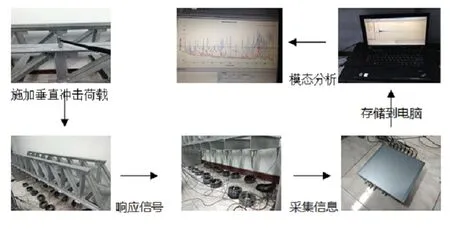
图9 桁架桥实验流程图

图10 (a) 5号传感器与12传感器的加速度时程响应比较

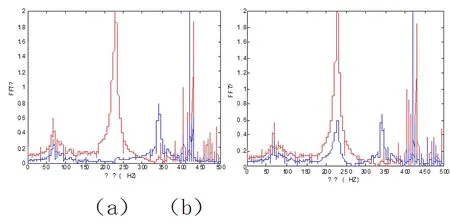
图11 (a) 5号节点与12号节点的传感器的FFT图

此桁架桥模态提取实验首先利用冲击锤对桁架桥模型施加一个垂直短时的冲击荷载，然后利用吸附在横梁上的加速度传感器获得桁架桥在竖直方向的自由响应信号，此时利用数据采集仪采集加速度响应历程数据并保存至笔记本电脑中，最后运用N-Modal模态分析软件提取桁架桥的频率与振型的参数信息，具体操作流程如下图9所示。

采样频率为100Hz,采样时间为10s，选取其中的5号节点、7号节点以及12号节点进行加速度响应分析，各节点的加速度响应曲线如下图10所示，红色线是5号节点上的传感器采集到的加速度响应信号曲线，蓝色线为7号与12号节点的传感器采集到的加速度响应信号曲线，从图中可以看出5号节点的传感器的响应信号与7、12节点的加速度信号存在一定区别，相对而言5号传感器位于振型的中心，故而采集得到的信息量更多。

为了验证仿真结果，当选取的主自由度个数为1个时，将最优主自由度以及其中部分非最优主自由度对应的目标函数值列于下表5所示。

表5 不同主自由度对应的目标函数值

从上表5中可知，最优主自由度为5号节点对应的竖向自由度，将传感器分别布置在最优的主自由度位置即5号节点的竖向自由度，与另外非最优位置的7号、12号节点的竖向自由度，得到不同的响应FFT图，如图11所示。

图11中，红色曲线为5号节点处的传感器的时程响应曲线，蓝色曲线分别为7、12号节点处传感器对应的响应信息。从每个图中都可以很清晰的看出，所用方法选择出的最优主自由度即5号节点的竖向自由度得到的频率成分更加丰富，说明了所采用方法的正确性。

5 结 论

采用文中的方法可得到优化的主自由度组合，表明贝叶斯统计系统识别方法能够很方便地识别出待识别结构建模参数的最优值以及相应的不确定性；信息熵指标能够定量的评估待识别参数的不确定性程度。增加主自由度的数量可减小结构待识别参数的不确定性。以桁架桥为例，表明能够适合于桥梁结构的主自由度优化选取问题求解。